Personalized Online Machine Learning

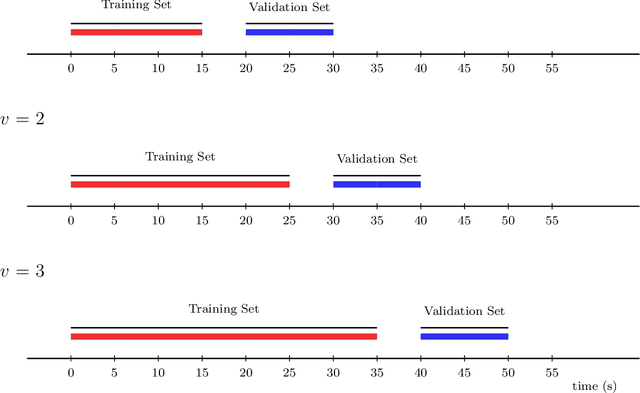
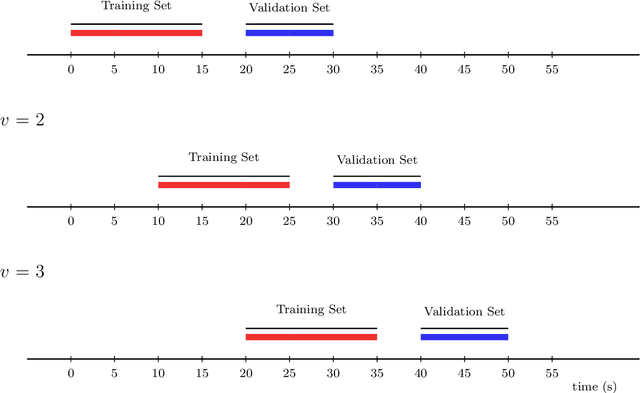
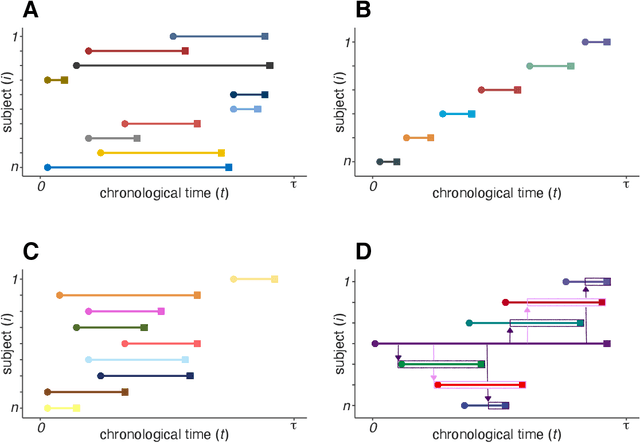
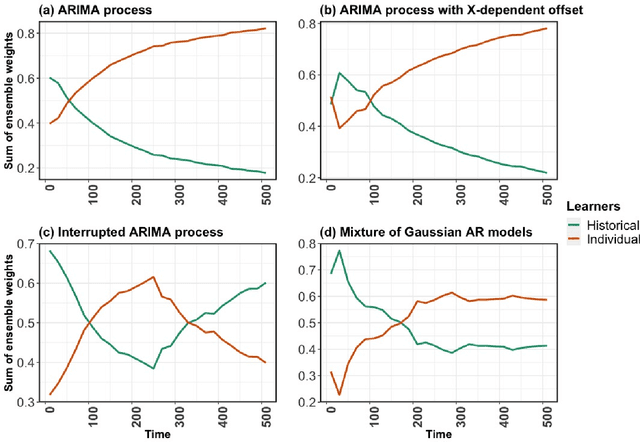
In this work, we introduce the Personalized Online Super Learner (POSL) -- an online ensembling algorithm for streaming data whose optimization procedure accommodates varying degrees of personalization. Namely, POSL optimizes predictions with respect to baseline covariates, so personalization can vary from completely individualized (i.e., optimization with respect to baseline covariate subject ID) to many individuals (i.e., optimization with respect to common baseline covariates). As an online algorithm, POSL learns in real-time. POSL can leverage a diversity of candidate algorithms, including online algorithms with different training and update times, fixed algorithms that are never updated during the procedure, pooled algorithms that learn from many individuals' time-series, and individualized algorithms that learn from within a single time-series. POSL's ensembling of this hybrid of base learning strategies depends on the amount of data collected, the stationarity of the time-series, and the mutual characteristics of a group of time-series. In essence, POSL decides whether to learn across samples, through time, or both, based on the underlying (unknown) structure in the data. For a wide range of simulations that reflect realistic forecasting scenarios, and in a medical data application, we examine the performance of POSL relative to other current ensembling and online learning methods. We show that POSL is able to provide reliable predictions for time-series data and adjust to changing data-generating environments. We further cultivate POSL's practicality by extending it to settings where time-series enter/exit dynamically over chronological time.

Estimation of population size based on capture recapture designs and evaluation of the estimation reliability

We propose a modern method to estimate population size based on capture-recapture designs of K samples. The observed data is formulated as a sample of n i.i.d. K-dimensional vectors of binary indicators, where the k-th component of each vector indicates the subject being caught by the k-th sample, such that only subjects with nonzero capture vectors are observed. The target quantity is the unconditional probability of the vector being nonzero across both observed and unobserved subjects. We cover models assuming a single constraint (identification assumption) on the K-dimensional distribution such that the target quantity is identified and the statistical model is unrestricted. We present solutions for linear and non-linear constraints commonly assumed to identify capture-recapture models, including no K-way interaction in linear and log-linear models, independence or conditional independence. We demonstrate that the choice of constraint has a dramatic impact on the value of the estimand, showing that it is crucial that the constraint is known to hold by design. For the commonly assumed constraint of no K-way interaction in a log-linear model, the statistical target parameter is only defined when each of the $2^K - 1$ observable capture patterns is present, and therefore suffers from the curse of dimensionality. We propose a targeted MLE based on undersmoothed lasso model to smooth across the cells while targeting the fit towards the single valued target parameter of interest. For each identification assumption, we provide simulated inference and confidence intervals to assess the performance on the estimator under correct and incorrect identifying assumptions. We apply the proposed method, alongside existing estimators, to estimate prevalence of a parasitic infection using multi-source surveillance data from a region in southwestern China, under the four identification assumptions.