Efficient Inference for Inverse Reinforcement Learning and Dynamic Discrete Choice Models

Inverse reinforcement learning (IRL) and dynamic discrete choice (DDC) models explain sequential decision-making by recovering reward functions that rationalize observed behavior. Flexible IRL methods typically rely on machine learning but provide no guarantees for valid inference, while classical DDC approaches impose restrictive parametric specifications and often require repeated dynamic programming. We develop a semiparametric framework for debiased inverse reinforcement learning that yields statistically efficient inference for a broad class of reward-dependent functionals in maximum entropy IRL and Gumbel-shock DDC models. We show that the log-behavior policy acts as a pseudo-reward that point-identifies policy value differences and, under a simple normalization, the reward itself. We then formalize these targets, including policy values under known and counterfactual softmax policies and functionals of the normalized reward, as smooth functionals of the behavior policy and transition kernel, establish pathwise differentiability, and derive their efficient influence functions. Building on this characterization, we construct automatic debiased machine-learning estimators that allow flexible nonparametric estimation of nuisance components while achieving $\sqrt{n}$-consistency, asymptotic normality, and semiparametric efficiency. Our framework extends classical inference for DDC models to nonparametric rewards and modern machine-learning tools, providing a unified and computationally tractable approach to statistical inference in IRL.

Near-Optimal Non-Parametric Sequential Tests and Confidence Sequences with Possibly Dependent Observations

Sequential testing, always-valid $p$-values, and confidence sequences promise flexible statistical inference and on-the-fly decision making. However, unlike fixed-$n$ inference based on asymptotic normality, existing sequential tests either make parametric assumptions and end up under-covering/over-rejecting when these fail or use non-parametric but conservative concentration inequalities and end up over-covering/under-rejecting. To circumvent these issues, we sidestep exact at-least-$\alpha$ coverage and focus on asymptotically exact coverage and asymptotic optimality. That is, we seek sequential tests whose probability of ever rejecting a true hypothesis asymptotically approaches $\alpha$ and whose expected time to reject a false hypothesis approaches a lower bound on all tests with asymptotic coverage at least $\alpha$, both under an appropriate asymptotic regime. We permit observations to be both non-parametric and dependent and focus on testing whether the observations form a martingale difference sequence. We propose the universal sequential probability ratio test (uSPRT), a slight modification to the normal-mixture sequential probability ratio test, where we add a burn-in period and adjust thresholds accordingly. We show that even in this very general setting, the uSPRT is asymptotically optimal under mild generic conditions. We apply the results to stabilized estimating equations to test means, treatment effects, etc. Our results also provide corresponding guarantees for the implied confidence sequences. Numerical simulations verify our guarantees and the benefits of the uSPRT over alternatives.

Adaptive Sequential Design for a Single Time-Series

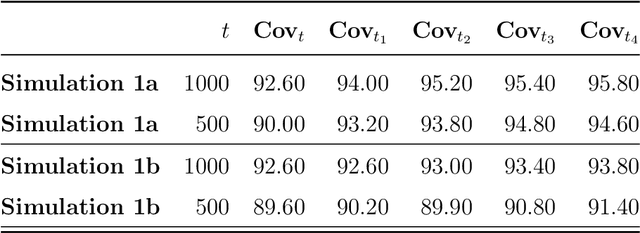
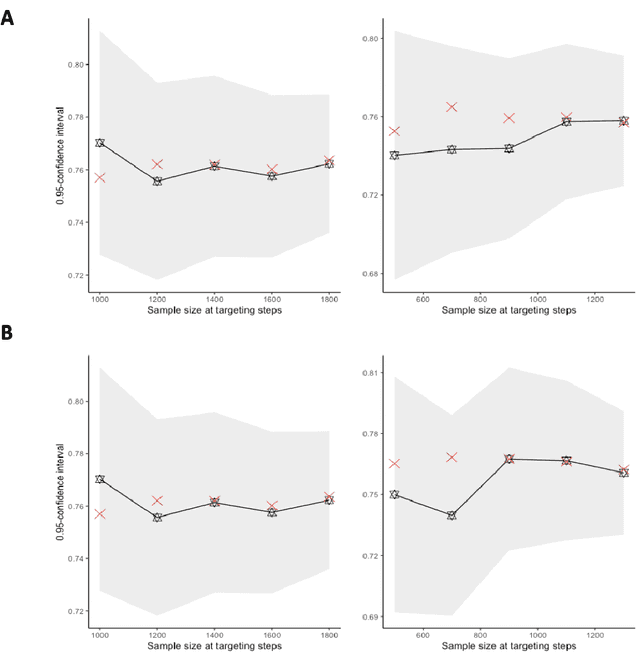
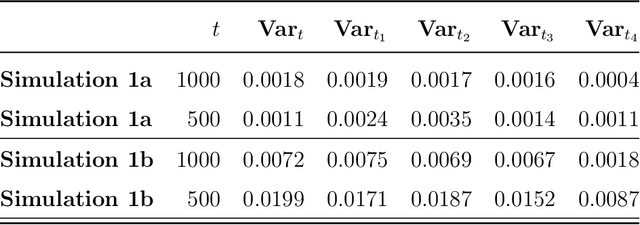
The current work is motivated by the need for robust statistical methods for precision medicine; as such, we address the need for statistical methods that provide actionable inference for a single unit at any point in time. We aim to learn an optimal, unknown choice of the controlled components of the design in order to optimize the expected outcome; with that, we adapt the randomization mechanism for future time-point experiments based on the data collected on the individual over time. Our results demonstrate that one can learn the optimal rule based on a single sample, and thereby adjust the design at any point t with valid inference for the mean target parameter. This work provides several contributions to the field of statistical precision medicine. First, we define a general class of averages of conditional causal parameters defined by the current context for the single unit time-series data. We define a nonparametric model for the probability distribution of the time-series under few assumptions, and aim to fully utilize the sequential randomization in the estimation procedure via the double robust structure of the efficient influence curve of the proposed target parameter. We present multiple exploration-exploitation strategies for assigning treatment, and methods for estimating the optimal rule. Lastly, we present the study of the data-adaptive inference on the mean under the optimal treatment rule, where the target parameter adapts over time in response to the observed context of the individual. Our target parameter is pathwise differentiable with an efficient influence function that is doubly robust - which makes it easier to estimate than previously proposed variations. We characterize the limit distribution of our estimator under a Donsker condition expressed in terms of a notion of bracketing entropy adapted to martingale settings.