Constructing optimal treatment length strategies to maximize quality-adjusted lifetimes

Real-world clinical decision making is a complex process that involves balancing the risks and benefits of treatments. Quality-adjusted lifetime is a composite outcome that combines patient quantity and quality of life, making it an attractive outcome in clinical research. We propose methods for constructing optimal treatment length strategies to maximize this outcome. Existing methods for estimating optimal treatment strategies for survival outcomes cannot be applied to a quality-adjusted lifetime due to induced informative censoring. We propose a weighted estimating equation that adjusts for both confounding and informative censoring. We also propose a nonparametric estimator of the mean counterfactual quality-adjusted lifetime survival curve under a given treatment length strategy, where the weights are estimated using an undersmoothed sieve-based estimator. We show that the estimator is asymptotically linear and provide a data-dependent undersmoothing criterion. We apply our method to obtain the optimal time for percutaneous endoscopic gastrostomy insertion in patients with amyotrophic lateral sclerosis.

Nonparametric estimation of a covariate-adjusted counterfactual treatment regimen response curve

Flexible estimation of the mean outcome under a treatment regimen (i.e., value function) is the key step toward personalized medicine. We define our target parameter as a conditional value function given a set of baseline covariates which we refer to as a stratum based value function. We focus on semiparametric class of decision rules and propose a sieve based nonparametric covariate adjusted regimen-response curve estimator within that class. Our work contributes in several ways. First, we propose an inverse probability weighted nonparametrically efficient estimator of the smoothed regimen-response curve function. We show that asymptotic linearity is achieved when the nuisance functions are undersmoothed sufficiently. Asymptotic and finite sample criteria for undersmoothing are proposed. Second, using Gaussian process theory, we propose simultaneous confidence intervals for the smoothed regimen-response curve function. Third, we provide consistency and convergence rate for the optimizer of the regimen-response curve estimator; this enables us to estimate an optimal semiparametric rule. The latter is important as the optimizer corresponds with the optimal dynamic treatment regimen. Some finite-sample properties are explored with simulations.

Causal inference for the expected number of recurrent events in the presence of a terminal event

We study causal inference and efficient estimation for the expected number of recurrent events in the presence of a terminal event. We define our estimand as the vector comprising both the expected number of recurrent events and the failure survival function evaluated along a sequence of landmark times. We identify the estimand in the presence of right-censoring and causal selection as an observed data functional under coarsening at random, derive the nonparametric efficiency bound, and propose a multiply-robust estimator that achieves the bound and permits nonparametric estimation of nuisance parameters. Throughout, no absolute continuity assumption is made on the underlying probability distributions of failure, censoring, or the observed data. Additionally, we derive the class of influence functions when the coarsening distribution is known and review how published estimators may belong to the class. Along the way, we highlight some interesting inconsistencies in the causal lifetime analysis literature.

Inference for relative sparsity

In healthcare, there is much interest in estimating policies, or mappings from covariates to treatment decisions. Recently, there is also interest in constraining these estimated policies to the standard of care, which generated the observed data. A relative sparsity penalty was proposed to derive policies that have sparse, explainable differences from the standard of care, facilitating justification of the new policy. However, the developers of this penalty only considered estimation, not inference. Here, we develop inference for the relative sparsity objective function, because characterizing uncertainty is crucial to applications in medicine. Further, in the relative sparsity work, the authors only considered the single-stage decision case; here, we consider the more general, multi-stage case. Inference is difficult, because the relative sparsity objective depends on the unpenalized value function, which is unstable and has infinite estimands in the binary action case. Further, one must deal with a non-differentiable penalty. To tackle these issues, we nest a weighted Trust Region Policy Optimization function within a relative sparsity objective, implement an adaptive relative sparsity penalty, and propose a sample-splitting framework for post-selection inference. We study the asymptotic behavior of our proposed approaches, perform extensive simulations, and analyze a real, electronic health record dataset.

Relative Sparsity for Medical Decision Problems

Existing statistical methods can be used to estimate a policy, or a mapping from covariates to decisions, which can then instruct decision makers. There is great interest in using such data-driven policies in healthcare. In healthcare, however, it is often important to explain to the healthcare provider, and to the patient, how a new policy differs from the current standard of care. This end is facilitated if one can pinpoint the aspects (i.e., parameters) of the policy that change most when moving from the standard of care to the new, suggested policy. To this end, we adapt ideas from Trust Region Policy Optimization. In our work, however, unlike in Trust Region Policy Optimization, the difference between the suggested policy and standard of care is required to be sparse, aiding with interpretability. In particular, we trade off between maximizing expected reward and minimizing the $L_1$ norm divergence between the parameters of the two policies. This yields "relative sparsity," where, as a function of a tuning parameter, $\lambda$, we can approximately control the number of parameters in our suggested policy that differ from their counterparts in the standard of care. We develop our methodology for the observational data setting. We propose a problem-specific criterion for selecting $\lambda$, perform simulations, and illustrate our method with a real, observational healthcare dataset, deriving a policy that is easy to explain in the context of the current standard of care. Our work promotes the adoption of data-driven decision aids, which have great potential to improve health outcomes.

Nonparametric inverse probability weighted estimators based on the highly adaptive lasso

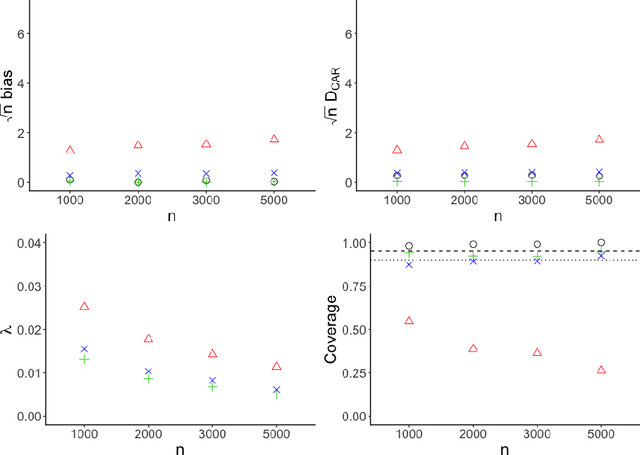
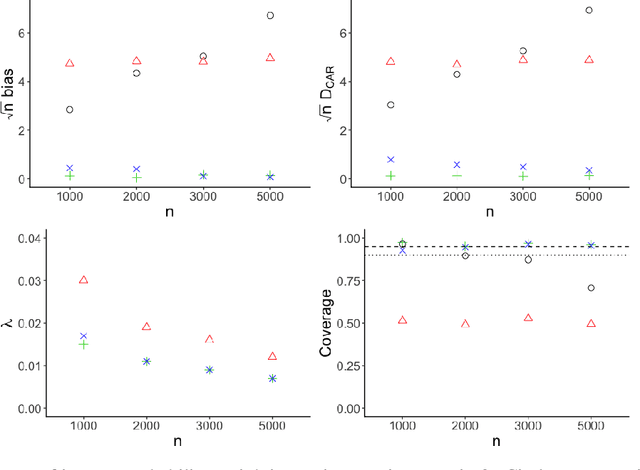
Inverse probability weighted estimators are the oldest and potentially most commonly used class of procedures for the estimation of causal effects. By adjusting for selection biases via a weighting mechanism, these procedures estimate an effect of interest by constructing a pseudo-population in which selection biases are eliminated. Despite their ease of use, these estimators require the correct specification of a model for the weighting mechanism, are known to be inefficient, and suffer from the curse of dimensionality. We propose a class of nonparametric inverse probability weighted estimators in which the weighting mechanism is estimated via undersmoothing of the highly adaptive lasso, a nonparametric regression function proven to converge at $n^{-1/3}$-rate to the true weighting mechanism. We demonstrate that our estimators are asymptotically linear with variance converging to the nonparametric efficiency bound. Unlike doubly robust estimators, our procedures require neither derivation of the efficient influence function nor specification of the conditional outcome model. Our theoretical developments have broad implications for the construction of efficient inverse probability weighted estimators in large statistical models and a variety of problem settings. We assess the practical performance of our estimators in simulation studies and demonstrate use of our proposed methodology with data from a large-scale epidemiologic study.

Robust Q-learning

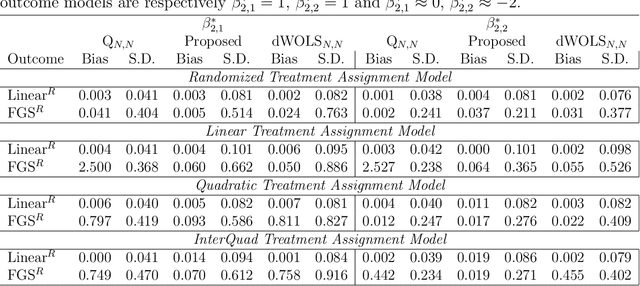
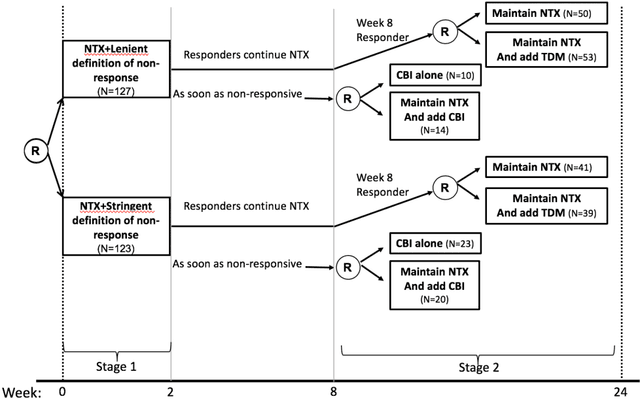
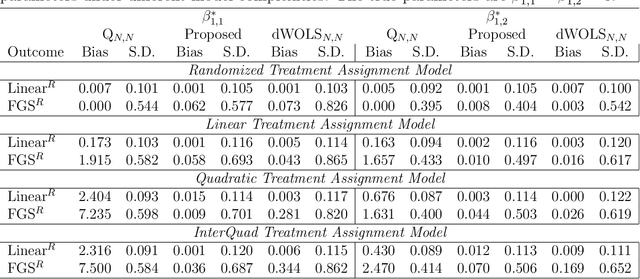
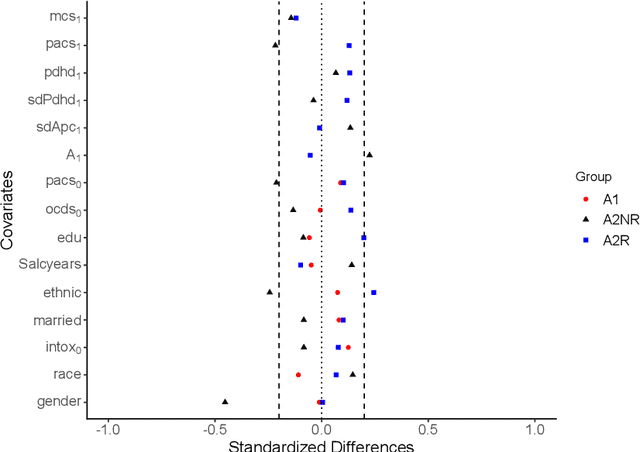
Q-learning is a regression-based approach that is widely used to formalize the development of an optimal dynamic treatment strategy. Finite dimensional working models are typically used to estimate certain nuisance parameters, and misspecification of these working models can result in residual confounding and/or efficiency loss. We propose a robust Q-learning approach which allows estimating such nuisance parameters using data-adaptive techniques. We study the asymptotic behavior of our estimators and provide simulation studies that highlight the need for and usefulness of the proposed method in practice. We use the data from the "Extending Treatment Effectiveness of Naltrexone" multi-stage randomized trial to illustrate our proposed methods.

Constructing Dynamic Treatment Regimes in Infinite-Horizon Settings

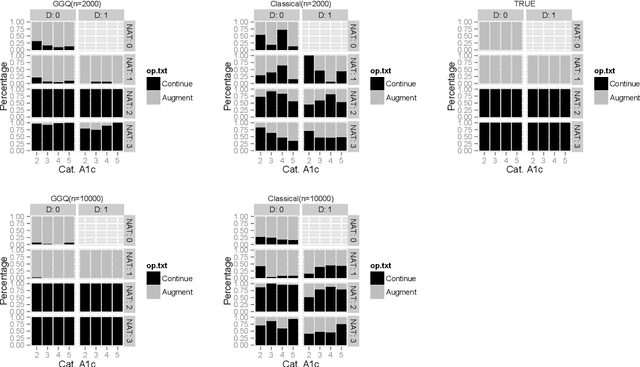
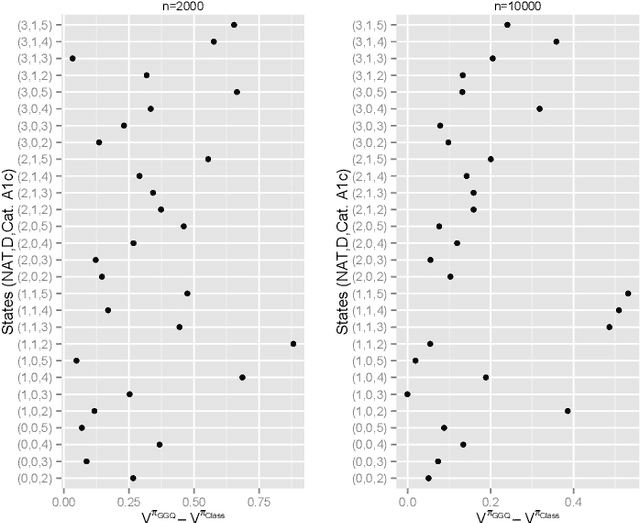
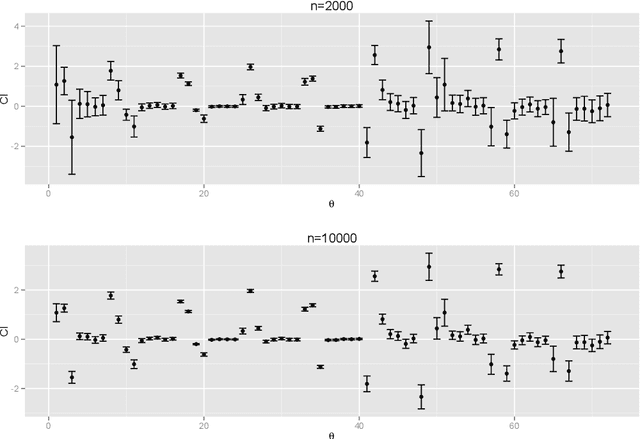
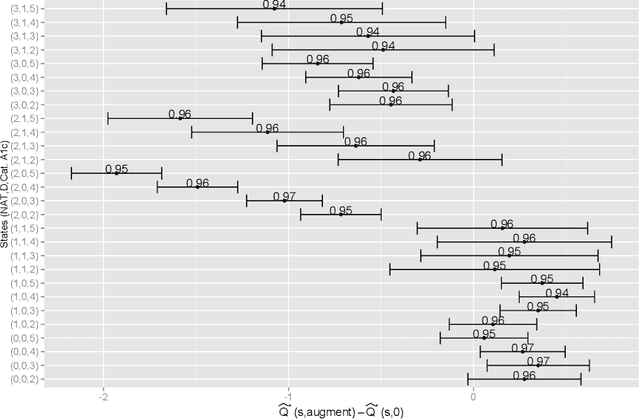
The application of existing methods for constructing optimal dynamic treatment regimes is limited to cases where investigators are interested in optimizing a utility function over a fixed period of time (finite horizon). In this manuscript, we develop an inferential procedure based on temporal difference residuals for optimal dynamic treatment regimes in infinite-horizon settings, where there is no a priori fixed end of follow-up point. The proposed method can be used to determine the optimal regime in chronic diseases where patients are monitored and treated throughout their life. We derive large sample results necessary for conducting inference. We also simulate a cohort of patients with diabetes to mimic the third wave of the National Health and Nutrition Examination Survey, and we examine the performance of the proposed method in controlling the level of hemoglobin A1c. Supplementary materials for this article are available online.