Constructing optimal treatment length strategies to maximize quality-adjusted lifetimes

Real-world clinical decision making is a complex process that involves balancing the risks and benefits of treatments. Quality-adjusted lifetime is a composite outcome that combines patient quantity and quality of life, making it an attractive outcome in clinical research. We propose methods for constructing optimal treatment length strategies to maximize this outcome. Existing methods for estimating optimal treatment strategies for survival outcomes cannot be applied to a quality-adjusted lifetime due to induced informative censoring. We propose a weighted estimating equation that adjusts for both confounding and informative censoring. We also propose a nonparametric estimator of the mean counterfactual quality-adjusted lifetime survival curve under a given treatment length strategy, where the weights are estimated using an undersmoothed sieve-based estimator. We show that the estimator is asymptotically linear and provide a data-dependent undersmoothing criterion. We apply our method to obtain the optimal time for percutaneous endoscopic gastrostomy insertion in patients with amyotrophic lateral sclerosis.

Nonparametric estimation of a covariate-adjusted counterfactual treatment regimen response curve

Flexible estimation of the mean outcome under a treatment regimen (i.e., value function) is the key step toward personalized medicine. We define our target parameter as a conditional value function given a set of baseline covariates which we refer to as a stratum based value function. We focus on semiparametric class of decision rules and propose a sieve based nonparametric covariate adjusted regimen-response curve estimator within that class. Our work contributes in several ways. First, we propose an inverse probability weighted nonparametrically efficient estimator of the smoothed regimen-response curve function. We show that asymptotic linearity is achieved when the nuisance functions are undersmoothed sufficiently. Asymptotic and finite sample criteria for undersmoothing are proposed. Second, using Gaussian process theory, we propose simultaneous confidence intervals for the smoothed regimen-response curve function. Third, we provide consistency and convergence rate for the optimizer of the regimen-response curve estimator; this enables us to estimate an optimal semiparametric rule. The latter is important as the optimizer corresponds with the optimal dynamic treatment regimen. Some finite-sample properties are explored with simulations.

Testing Sparsity Assumptions in Bayesian Networks

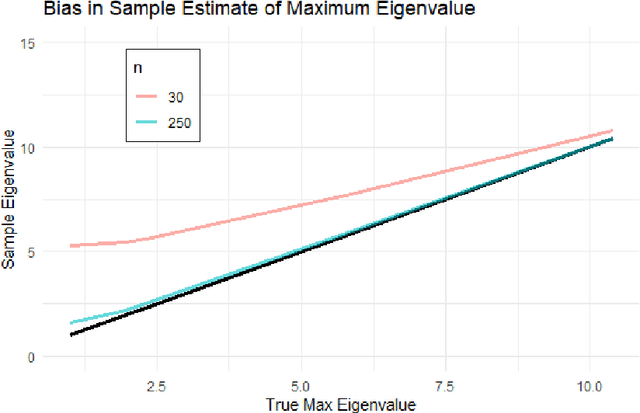
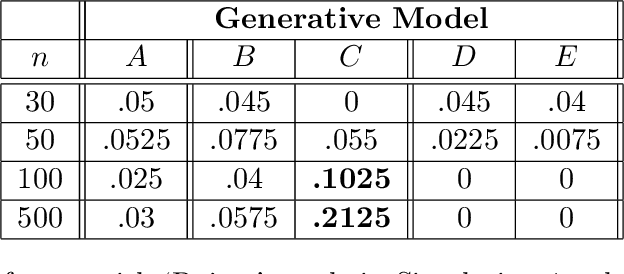
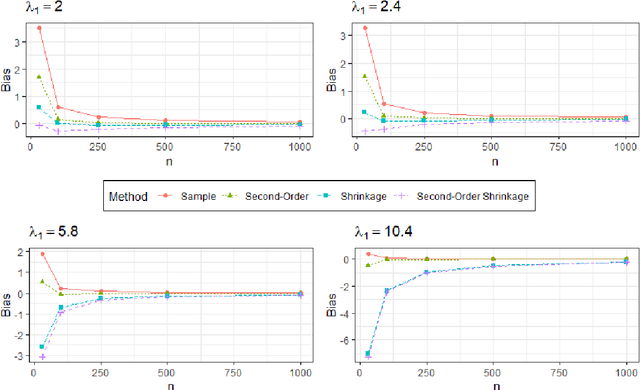
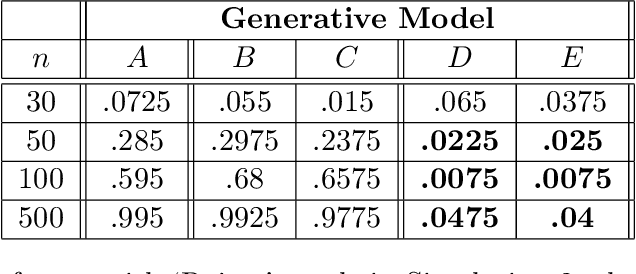
Bayesian network (BN) structure discovery algorithms typically either make assumptions about the sparsity of the true underlying network, or are limited by computational constraints to networks with a small number of variables. While these sparsity assumptions can take various forms, frequently the assumptions focus on an upper bound for the maximum in-degree of the underlying graph $\nabla_G$. Theorem 2 in Duttweiler et. al. (2023) demonstrates that the largest eigenvalue of the normalized inverse covariance matrix ($\Omega$) of a linear BN is a lower bound for $\nabla_G$. Building on this result, this paper provides the asymptotic properties of, and a debiasing procedure for, the sample eigenvalues of $\Omega$, leading to a hypothesis test that may be used to determine if the BN has max in-degree greater than 1. A linear BN structure discovery workflow is suggested in which the investigator uses this hypothesis test to aid in selecting an appropriate structure discovery algorithm. The hypothesis test performance is evaluated through simulations and the workflow is demonstrated on data from a human psoriasis study.