Sally W. Thurston
Testing Sparsity Assumptions in Bayesian Networks
Jul 12, 2023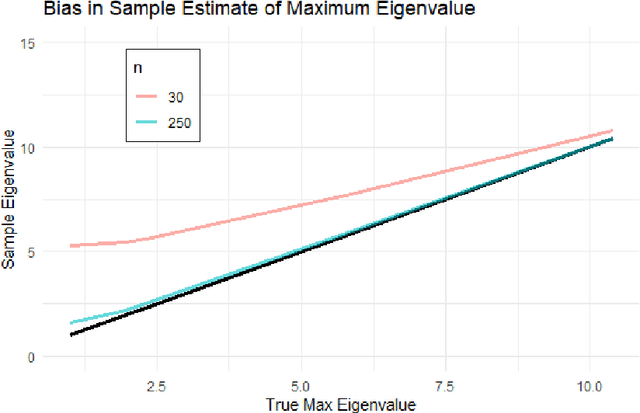
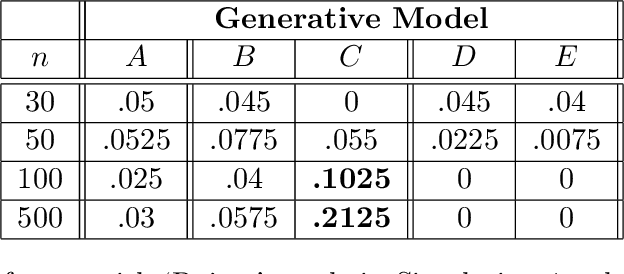
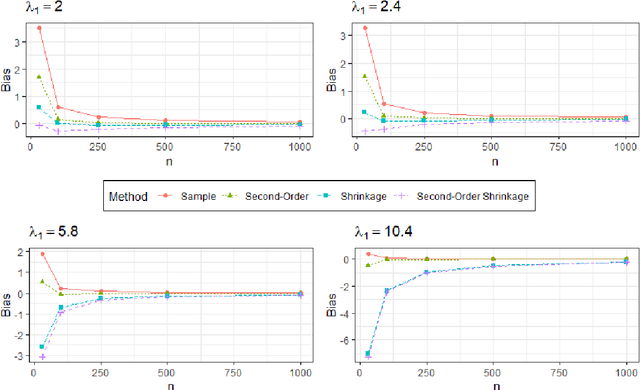
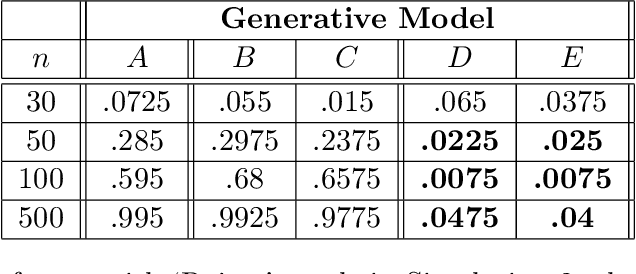
Abstract:Bayesian network (BN) structure discovery algorithms typically either make assumptions about the sparsity of the true underlying network, or are limited by computational constraints to networks with a small number of variables. While these sparsity assumptions can take various forms, frequently the assumptions focus on an upper bound for the maximum in-degree of the underlying graph $\nabla_G$. Theorem 2 in Duttweiler et. al. (2023) demonstrates that the largest eigenvalue of the normalized inverse covariance matrix ($\Omega$) of a linear BN is a lower bound for $\nabla_G$. Building on this result, this paper provides the asymptotic properties of, and a debiasing procedure for, the sample eigenvalues of $\Omega$, leading to a hypothesis test that may be used to determine if the BN has max in-degree greater than 1. A linear BN structure discovery workflow is suggested in which the investigator uses this hypothesis test to aid in selecting an appropriate structure discovery algorithm. The hypothesis test performance is evaluated through simulations and the workflow is demonstrated on data from a human psoriasis study.
Inference for relative sparsity
Jun 25, 2023



Abstract:In healthcare, there is much interest in estimating policies, or mappings from covariates to treatment decisions. Recently, there is also interest in constraining these estimated policies to the standard of care, which generated the observed data. A relative sparsity penalty was proposed to derive policies that have sparse, explainable differences from the standard of care, facilitating justification of the new policy. However, the developers of this penalty only considered estimation, not inference. Here, we develop inference for the relative sparsity objective function, because characterizing uncertainty is crucial to applications in medicine. Further, in the relative sparsity work, the authors only considered the single-stage decision case; here, we consider the more general, multi-stage case. Inference is difficult, because the relative sparsity objective depends on the unpenalized value function, which is unstable and has infinite estimands in the binary action case. Further, one must deal with a non-differentiable penalty. To tackle these issues, we nest a weighted Trust Region Policy Optimization function within a relative sparsity objective, implement an adaptive relative sparsity penalty, and propose a sample-splitting framework for post-selection inference. We study the asymptotic behavior of our proposed approaches, perform extensive simulations, and analyze a real, electronic health record dataset.
Relative Sparsity for Medical Decision Problems
Nov 29, 2022Abstract:Existing statistical methods can be used to estimate a policy, or a mapping from covariates to decisions, which can then instruct decision makers. There is great interest in using such data-driven policies in healthcare. In healthcare, however, it is often important to explain to the healthcare provider, and to the patient, how a new policy differs from the current standard of care. This end is facilitated if one can pinpoint the aspects (i.e., parameters) of the policy that change most when moving from the standard of care to the new, suggested policy. To this end, we adapt ideas from Trust Region Policy Optimization. In our work, however, unlike in Trust Region Policy Optimization, the difference between the suggested policy and standard of care is required to be sparse, aiding with interpretability. In particular, we trade off between maximizing expected reward and minimizing the $L_1$ norm divergence between the parameters of the two policies. This yields "relative sparsity," where, as a function of a tuning parameter, $\lambda$, we can approximately control the number of parameters in our suggested policy that differ from their counterparts in the standard of care. We develop our methodology for the observational data setting. We propose a problem-specific criterion for selecting $\lambda$, perform simulations, and illustrate our method with a real, observational healthcare dataset, deriving a policy that is easy to explain in the context of the current standard of care. Our work promotes the adoption of data-driven decision aids, which have great potential to improve health outcomes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge