Causal inference for the expected number of recurrent events in the presence of a terminal event

We study causal inference and efficient estimation for the expected number of recurrent events in the presence of a terminal event. We define our estimand as the vector comprising both the expected number of recurrent events and the failure survival function evaluated along a sequence of landmark times. We identify the estimand in the presence of right-censoring and causal selection as an observed data functional under coarsening at random, derive the nonparametric efficiency bound, and propose a multiply-robust estimator that achieves the bound and permits nonparametric estimation of nuisance parameters. Throughout, no absolute continuity assumption is made on the underlying probability distributions of failure, censoring, or the observed data. Additionally, we derive the class of influence functions when the coarsening distribution is known and review how published estimators may belong to the class. Along the way, we highlight some interesting inconsistencies in the causal lifetime analysis literature.

Regression Trees for Cumulative Incidence Functions

The use of cumulative incidence functions for characterizing the risk of one type of event in the presence of others has become increasingly popular over the past decade. The problems of modeling, estimation and inference have been treated using parametric, nonparametric and semi-parametric methods. Efforts to develop suitable extensions of machine learning methods, such as regression trees and related ensemble methods, have begun only recently. In this paper, we develop a novel approach to building regression trees for estimating cumulative incidence curves in a competing risks setting. The proposed methods employ augmented estimators of the Brier score risk as the primary basis for building and pruning trees. The proposed methods are easily implemented using the R statistical software package. Simulation studies demonstrate the utility of our approach in the competing risks setting. Data from the Radiation Therapy Oncology Group (trial 9410) is used to illustrate these new methods.

Robust Q-learning

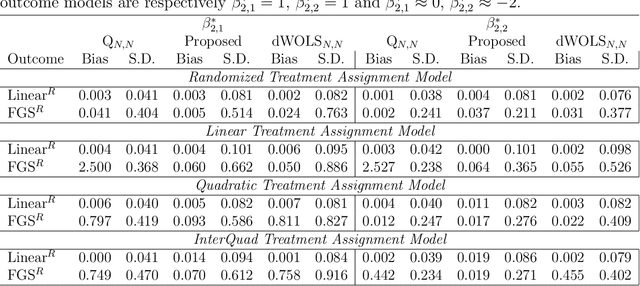
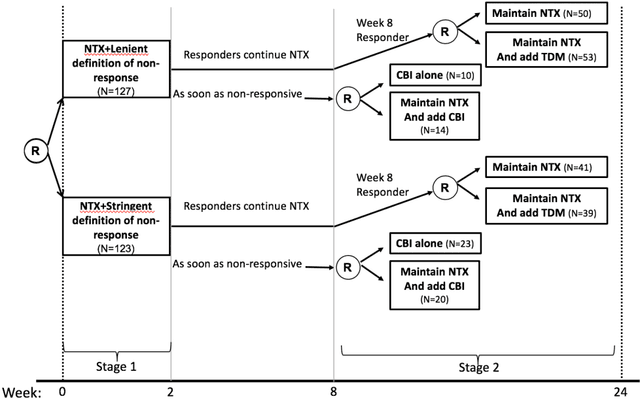
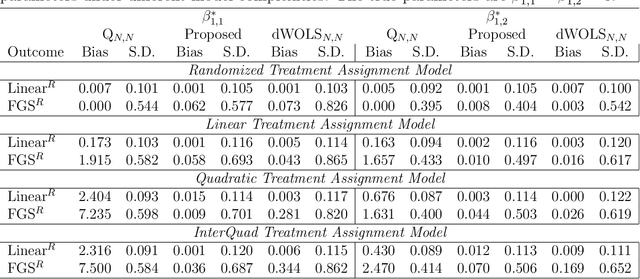
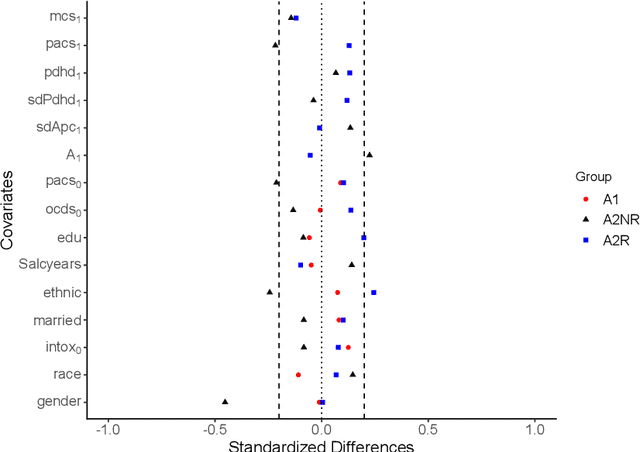
Q-learning is a regression-based approach that is widely used to formalize the development of an optimal dynamic treatment strategy. Finite dimensional working models are typically used to estimate certain nuisance parameters, and misspecification of these working models can result in residual confounding and/or efficiency loss. We propose a robust Q-learning approach which allows estimating such nuisance parameters using data-adaptive techniques. We study the asymptotic behavior of our estimators and provide simulation studies that highlight the need for and usefulness of the proposed method in practice. We use the data from the "Extending Treatment Effectiveness of Naltrexone" multi-stage randomized trial to illustrate our proposed methods.