Targeting Learning: Robust Statistics for Reproducible Research

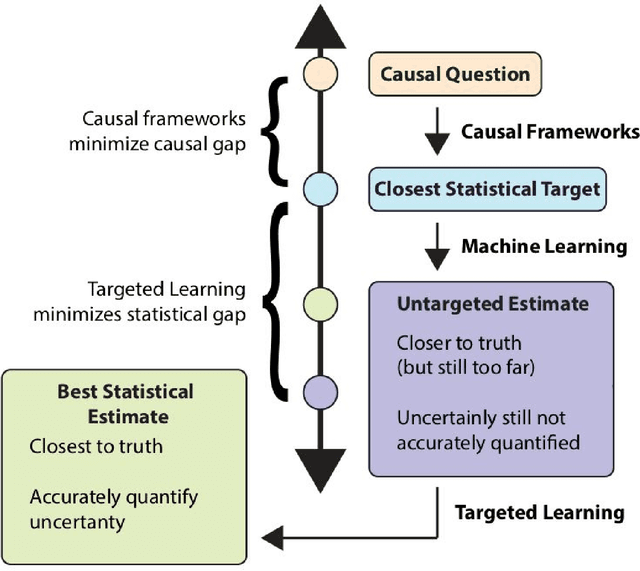
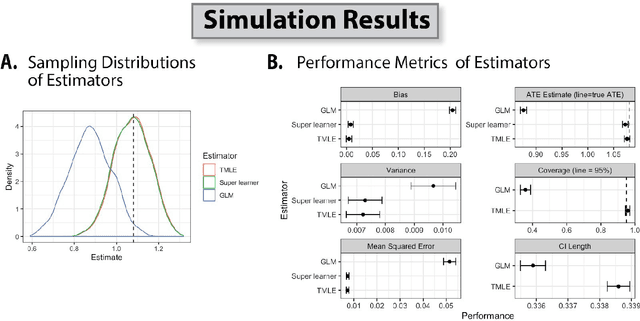
Targeted Learning is a subfield of statistics that unifies advances in causal inference, machine learning and statistical theory to help answer scientifically impactful questions with statistical confidence. Targeted Learning is driven by complex problems in data science and has been implemented in a diversity of real-world scenarios: observational studies with missing treatments and outcomes, personalized interventions, longitudinal settings with time-varying treatment regimes, survival analysis, adaptive randomized trials, mediation analysis, and networks of connected subjects. In contrast to the (mis)application of restrictive modeling strategies that dominate the current practice of statistics, Targeted Learning establishes a principled standard for statistical estimation and inference (i.e., confidence intervals and p-values). This multiply robust approach is accompanied by a guiding roadmap and a burgeoning software ecosystem, both of which provide guidance on the construction of estimators optimized to best answer the motivating question. The roadmap of Targeted Learning emphasizes tailoring statistical procedures so as to minimize their assumptions, carefully grounding them only in the scientific knowledge available. The end result is a framework that honestly reflects the uncertainty in both the background knowledge and the available data in order to draw reliable conclusions from statistical analyses - ultimately enhancing the reproducibility and rigor of scientific findings.

Data-adaptive statistics for multiple hypothesis testing in high-dimensional settings

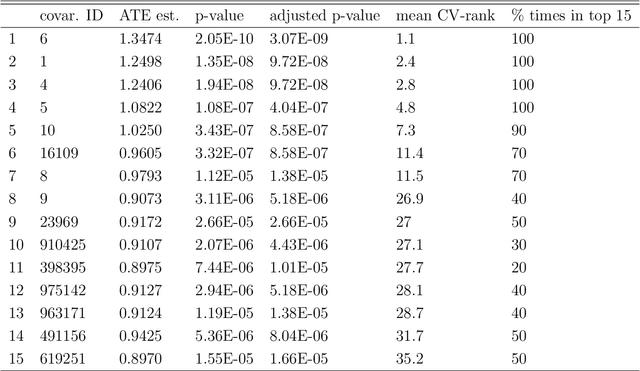
Current statistical inference problems in areas like astronomy, genomics, and marketing routinely involve the simultaneous testing of thousands -- even millions -- of null hypotheses. For high-dimensional multivariate distributions, these hypotheses may concern a wide range of parameters, with complex and unknown dependence structures among variables. In analyzing such hypothesis testing procedures, gains in efficiency and power can be achieved by performing variable reduction on the set of hypotheses prior to testing. We present in this paper an approach using data-adaptive multiple testing that serves exactly this purpose. This approach applies data mining techniques to screen the full set of covariates on equally sized partitions of the whole sample via cross-validation. This generalized screening procedure is used to create average ranks for covariates, which are then used to generate a reduced (sub)set of hypotheses, from which we compute test statistics that are subsequently subjected to standard multiple testing corrections. The principal advantage of this methodology lies in its providing valid statistical inference without the \textit{a priori} specifying which hypotheses will be tested. Here, we present the theoretical details of this approach, confirm its validity via a simulation study, and exemplify its use by applying it to the analysis of data on microRNA differential expression.