Data-adaptive statistics for multiple hypothesis testing in high-dimensional settings
Paper and Code
Apr 24, 2017
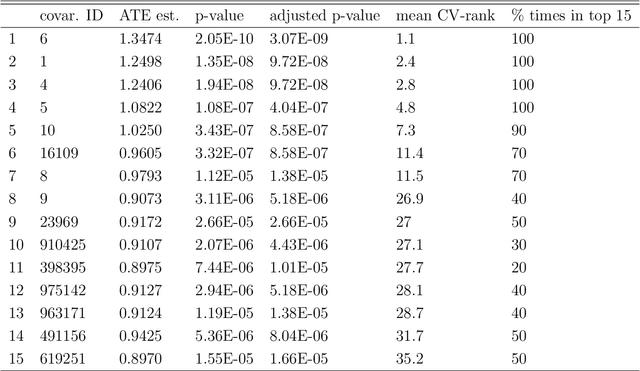


Current statistical inference problems in areas like astronomy, genomics, and marketing routinely involve the simultaneous testing of thousands -- even millions -- of null hypotheses. For high-dimensional multivariate distributions, these hypotheses may concern a wide range of parameters, with complex and unknown dependence structures among variables. In analyzing such hypothesis testing procedures, gains in efficiency and power can be achieved by performing variable reduction on the set of hypotheses prior to testing. We present in this paper an approach using data-adaptive multiple testing that serves exactly this purpose. This approach applies data mining techniques to screen the full set of covariates on equally sized partitions of the whole sample via cross-validation. This generalized screening procedure is used to create average ranks for covariates, which are then used to generate a reduced (sub)set of hypotheses, from which we compute test statistics that are subsequently subjected to standard multiple testing corrections. The principal advantage of this methodology lies in its providing valid statistical inference without the \textit{a priori} specifying which hypotheses will be tested. Here, we present the theoretical details of this approach, confirm its validity via a simulation study, and exemplify its use by applying it to the analysis of data on microRNA differential expression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge