Weighting-Based Identification and Estimation in Graphical Models of Missing Data

We propose a constructive algorithm for identifying complete data distributions in graphical models of missing data. The complete data distribution is unrestricted, while the missingness mechanism is assumed to factorize according to a conditional directed acyclic graph. Our approach follows an interventionist perspective in which missingness indicators are treated as variables that can be intervened on. A central challenge in this setting is that sequences of interventions on missingness indicators may induce and propagate selection bias, so that identification can fail even when a propensity score is invariant to available interventions. To address this challenge, we introduce a tree-based identification algorithm that explicitly tracks the creation and propagation of selection bias and determines whether it can be avoided through admissible intervention strategies. The resulting tree provides both a diagnostic and a constructive characterization of identifiability under a given missingness mechanism. Building on these results, we develop recursive inverse probability weighting procedures that mirror the intervention logic of the identification algorithm, yielding valid estimating equations for both the missingness mechanism and functionals of the complete data distribution. Simulation studies and a real-data application illustrate the practical performance of the proposed methods. An accompanying R package, flexMissing, implements all proposed procedures.

Causal Inference with the "Napkin Graph"

Unmeasured confounding can render identification strategies based on adjustment functionals invalid. We study the "Napkin graph", a causal structure that encapsulates patterns of M-bias, instrumental variables, and the classical back-door and front-door models within a single graphical framework, yet requires a nonstandard identification strategy: the average treatment effect is expressed as a ratio of two g-formulas. We develop novel estimators for this functional, including doubly robust one-step and targeted minimum loss-based estimators that remain asymptotically linear when nuisance functions are estimated at slower-than-parametric rates using machine learning. We also show how a generalized independence restriction encoded by the Napkin graph, known as a Verma constraint, can be exploited to improve efficiency, illustrating more generally how such constraints in hidden variable DAGs can inform semiparametric inference. The proposed methods are validated through simulations and applied to the Finnish Life Course study to estimate the effect of educational attainment on income. An accompanying R package, napkincausal, implements all proposed procedures.

Average Causal Effect Estimation in DAGs with Hidden Variables: Extensions of Back-Door and Front-Door Criteria

The identification theory for causal effects in directed acyclic graphs (DAGs) with hidden variables is well-developed, but methods for estimating and inferring functionals beyond the g-formula remain limited. Previous studies have proposed semiparametric estimators for identifiable functionals in a broad class of DAGs with hidden variables. While demonstrating double robustness in some models, existing estimators face challenges, particularly with density estimation and numerical integration for continuous variables, and their estimates may fall outside the parameter space of the target estimand. Their asymptotic properties are also underexplored, especially when using flexible statistical and machine learning models for nuisance estimation. This study addresses these challenges by introducing novel one-step corrected plug-in and targeted minimum loss-based estimators of causal effects for a class of DAGs that extend classical back-door and front-door criteria (known as the treatment primal fixability criterion in prior literature). These estimators leverage machine learning to minimize modeling assumptions while ensuring key statistical properties such as asymptotic linearity, double robustness, efficiency, and staying within the bounds of the target parameter space. We establish conditions for nuisance functional estimates in terms of L2(P)-norms to achieve root-n consistent causal effect estimates. To facilitate practical application, we have developed the flexCausal package in R.

Targeted Machine Learning for Average Causal Effect Estimation Using the Front-Door Functional

Evaluating the average causal effect (ACE) of a treatment on an outcome often involves overcoming the challenges posed by confounding factors in observational studies. A traditional approach uses the back-door criterion, seeking adjustment sets to block confounding paths between treatment and outcome. However, this method struggles with unmeasured confounders. As an alternative, the front-door criterion offers a solution, even in the presence of unmeasured confounders between treatment and outcome. This method relies on identifying mediators that are not directly affected by these confounders and that completely mediate the treatment's effect. Here, we introduce novel estimation strategies for the front-door criterion based on the targeted minimum loss-based estimation theory. Our estimators work across diverse scenarios, handling binary, continuous, and multivariate mediators. They leverage data-adaptive machine learning algorithms, minimizing assumptions and ensuring key statistical properties like asymptotic linearity, double-robustness, efficiency, and valid estimates within the target parameter space. We establish conditions under which the nuisance functional estimations ensure the root n-consistency of ACE estimators. Our numerical experiments show the favorable finite sample performance of the proposed estimators. We demonstrate the applicability of these estimators to analyze the effect of early stage academic performance on future yearly income using data from the Finnish Social Science Data Archive.

Sufficient Identification Conditions and Semiparametric Estimation under Missing Not at Random Mechanisms

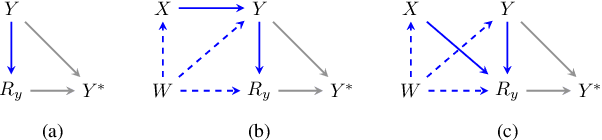
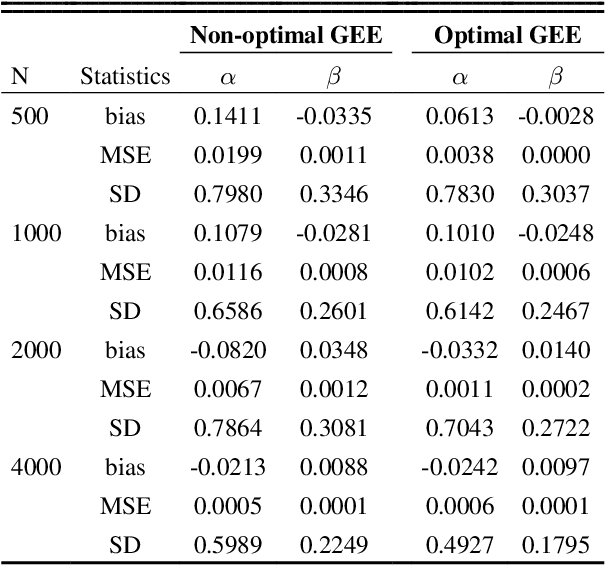
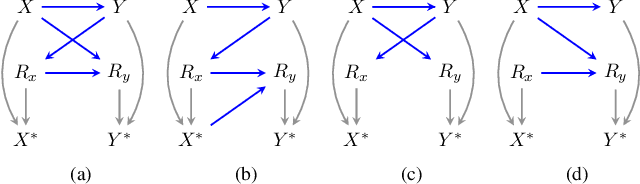
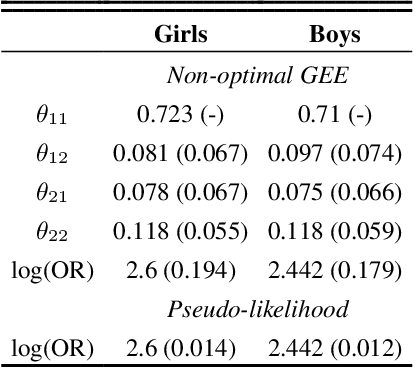
Conducting valid statistical analyses is challenging in the presence of missing-not-at-random (MNAR) data, where the missingness mechanism is dependent on the missing values themselves even conditioned on the observed data. Here, we consider a MNAR model that generalizes several prior popular MNAR models in two ways: first, it is less restrictive in terms of statistical independence assumptions imposed on the underlying joint data distribution, and second, it allows for all variables in the observed sample to have missing values. This MNAR model corresponds to a so-called criss-cross structure considered in the literature on graphical models of missing data that prevents nonparametric identification of the entire missing data model. Nonetheless, part of the complete-data distribution remains nonparametrically identifiable. By exploiting this fact and considering a rich class of exponential family distributions, we establish sufficient conditions for identification of the complete-data distribution as well as the entire missingness mechanism. We then propose methods for testing the independence restrictions encoded in such models using odds ratio as our parameter of interest. We adopt two semiparametric approaches for estimating the odds ratio parameter and establish the corresponding asymptotic theories: one involves maximizing a conditional likelihood with order statistics and the other uses estimating equations. The utility of our methods is illustrated via simulation studies.