Network Causal Effect Estimation In Graphical Models Of Contagion And Latent Confounding

A key question in many network studies is whether the observed correlations between units are primarily due to contagion or latent confounding. Here, we study this question using a segregated graph (Shpitser, 2015) representation of these mechanisms, and examine how uncertainty about the true underlying mechanism impacts downstream computation of network causal effects, particularly under full interference -- settings where we only have a single realization of a network and each unit may depend on any other unit in the network. Under certain assumptions about asymptotic growth of the network, we derive likelihood ratio tests that can be used to identify whether different sets of variables -- confounders, treatments, and outcomes -- across units exhibit dependence due to contagion or latent confounding. We then propose network causal effect estimation strategies that provide unbiased and consistent estimates if the dependence mechanisms are either known or correctly inferred using our proposed tests. Together, the proposed methods allow network effect estimation in a wider range of full interference scenarios that have not been considered in prior work. We evaluate the effectiveness of our methods with synthetic data and the validity of our assumptions using real-world networks.

Proximal Causal Inference With Text Data

Recent text-based causal methods attempt to mitigate confounding bias by including unstructured text data as proxies of confounding variables that are partially or imperfectly measured. These approaches assume analysts have supervised labels of the confounders given text for a subset of instances, a constraint that is not always feasible due to data privacy or cost. Here, we address settings in which an important confounding variable is completely unobserved. We propose a new causal inference method that splits pre-treatment text data, infers two proxies from two zero-shot models on the separate splits, and applies these proxies in the proximal g-formula. We prove that our text-based proxy method satisfies identification conditions required by the proximal g-formula while other seemingly reasonable proposals do not. We evaluate our method in synthetic and semi-synthetic settings and find that it produces estimates with low bias. This combination of proximal causal inference and zero-shot classifiers is novel (to our knowledge) and expands the set of text-specific causal methods available to practitioners.

RCT Rejection Sampling for Causal Estimation Evaluation

Confounding is a significant obstacle to unbiased estimation of causal effects from observational data. For settings with high-dimensional covariates -- such as text data, genomics, or the behavioral social sciences -- researchers have proposed methods to adjust for confounding by adapting machine learning methods to the goal of causal estimation. However, empirical evaluation of these adjustment methods has been challenging and limited. In this work, we build on a promising empirical evaluation strategy that simplifies evaluation design and uses real data: subsampling randomized controlled trials (RCTs) to create confounded observational datasets while using the average causal effects from the RCTs as ground-truth. We contribute a new sampling algorithm, which we call RCT rejection sampling, and provide theoretical guarantees that causal identification holds in the observational data to allow for valid comparisons to the ground-truth RCT. Using synthetic data, we show our algorithm indeed results in low bias when oracle estimators are evaluated on the confounded samples, which is not always the case for a previously proposed algorithm. In addition to this identification result, we highlight several finite data considerations for evaluation designers who plan to use RCT rejection sampling on their own datasets. As a proof of concept, we implement an example evaluation pipeline and walk through these finite data considerations with a novel, real-world RCT -- which we release publicly -- consisting of approximately 70k observations and text data as high-dimensional covariates. Together, these contributions build towards a broader agenda of improved empirical evaluation for causal estimation.

Causal and counterfactual views of missing data models

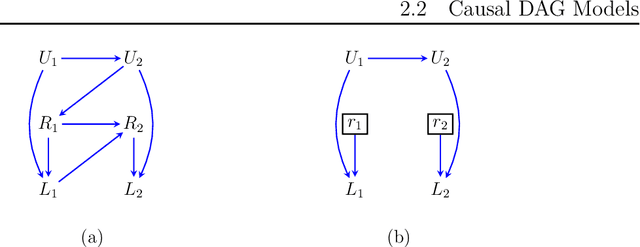
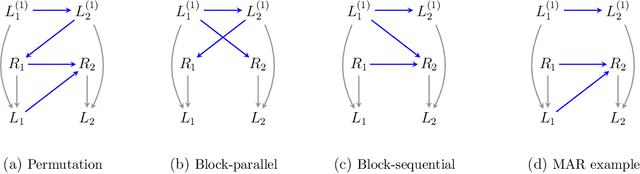
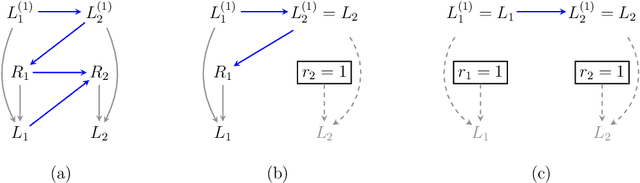
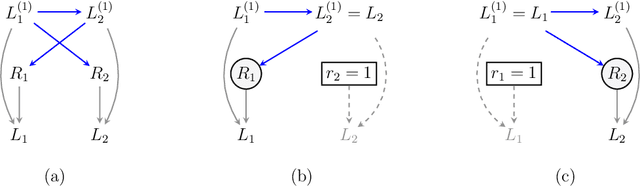
It is often said that the fundamental problem of causal inference is a missing data problem -- the comparison of responses to two hypothetical treatment assignments is made difficult because for every experimental unit only one potential response is observed. In this paper, we consider the implications of the converse view: that missing data problems are a form of causal inference. We make explicit how the missing data problem of recovering the complete data law from the observed law can be viewed as identification of a joint distribution over counterfactual variables corresponding to values had we (possibly contrary to fact) been able to observe them. Drawing analogies with causal inference, we show how identification assumptions in missing data can be encoded in terms of graphical models defined over counterfactual and observed variables. We review recent results in missing data identification from this viewpoint. In doing so, we note interesting similarities and differences between missing data and causal identification theories.

On Testability of the Front-Door Model via Verma Constraints

The front-door criterion can be used to identify and compute causal effects despite the existence of unmeasured confounders between a treatment and outcome. However, the key assumptions -- (i) the existence of a variable (or set of variables) that fully mediates the effect of the treatment on the outcome, and (ii) which simultaneously does not suffer from similar issues of confounding as the treatment-outcome pair -- are often deemed implausible. This paper explores the testability of these assumptions. We show that under mild conditions involving an auxiliary variable, the assumptions encoded in the front-door model (and simple extensions of it) may be tested via generalized equality constraints a.k.a Verma constraints. We propose two goodness-of-fit tests based on this observation, and evaluate the efficacy of our proposal on real and synthetic data. We also provide theoretical and empirical comparisons to instrumental variable approaches to handling unmeasured confounding.

On Testability and Goodness of Fit Tests in Missing Data Models

Significant progress has been made in developing identification and estimation techniques for missing data problems where modeling assumptions can be described via a directed acyclic graph. The validity of results using such techniques rely on the assumptions encoded by the graph holding true; however, verification of these assumptions has not received sufficient attention in prior work. In this paper, we provide new insights on the testable implications of three broad classes of missing data graphical models, and design goodness-of-fit tests around them. The classes of models explored are: sequential missing-at-random and missing-not-at-random models which can be used for modeling longitudinal studies with dropout/censoring, and a kind of no self-censoring model which can be applied to cross-sectional studies and surveys.

Differentiable Causal Discovery Under Unmeasured Confounding

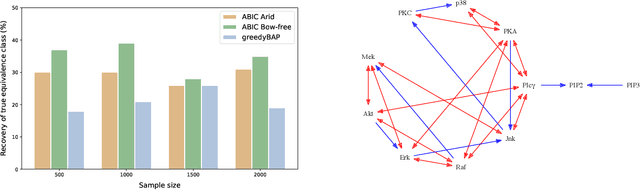
The data drawn from biological, economic, and social systems are often confounded due to the presence of unmeasured variables. Prior work in causal discovery has focused on discrete search procedures for selecting acyclic directed mixed graphs (ADMGs), specifically ancestral ADMGs, that encode ordinary conditional independence constraints among the observed variables of the system. However, confounded systems also exhibit more general equality restrictions that cannot be represented via these graphs, placing a limit on the kinds of structures that can be learned using ancestral ADMGs. In this work, we derive differentiable algebraic constraints that fully characterize the space of ancestral ADMGs, as well as more general classes of ADMGs, arid ADMGs and bow-free ADMGs, that capture all equality restrictions on the observed variables. We use these constraints to cast causal discovery as a continuous optimization problem and design differentiable procedures to find the best fitting ADMG when the data comes from a confounded linear system of equations with correlated errors. We demonstrate the efficacy of our method through simulations and application to a protein expression dataset.

Full Law Identification In Graphical Models Of Missing Data: Completeness Results

Missing data has the potential to affect analyses conducted in all fields of scientific study, including healthcare, economics, and the social sciences. Several approaches to unbiased inference in the presence of non-ignorable missingness rely on the specification of the target distribution and its missingness process as a probability distribution that factorizes with respect to a directed acyclic graph. In this paper, we address the longstanding question of the characterization of models that are identifiable within this class of missing data distributions. We provide the first completeness result in this field of study -- necessary and sufficient graphical conditions under which, the full data distribution can be recovered from the observed data distribution. We then simultaneously address issues that may arise due to the presence of both missing data and unmeasured confounding, by extending these graphical conditions and proofs of completeness, to settings where some variables are not just missing, but completely unobserved.

Semiparametric Inference For Causal Effects In Graphical Models With Hidden Variables

The last decade witnessed the development of algorithms that completely solve the identifiability problem for causal effects in hidden variable causal models associated with directed acyclic graphs. However, much of this machinery remains underutilized in practice owing to the complexity of estimating identifying functionals yielded by these algorithms. In this paper, we provide simple graphical criteria and semiparametric estimators that bridge the gap between identification and estimation for causal effects involving a single treatment and a single outcome. First, we provide influence function based doubly robust estimators that cover a significant subset of hidden variable causal models where the effect is identifiable. We further characterize an important subset of this class for which we demonstrate how to derive the estimator with the lowest asymptotic variance, i.e., one that achieves the semiparametric efficiency bound. Finally, we provide semiparametric estimators for any single treatment causal effect parameter identified via the aforementioned algorithms. The resulting estimators resemble influence function based estimators that are sequentially reweighted, and exhibit a partial double robustness property, provided the parts of the likelihood corresponding to a set of weight models are correctly specified. Our methods are easy to implement and we demonstrate their utility through simulations.

Identification In Missing Data Models Represented By Directed Acyclic Graphs

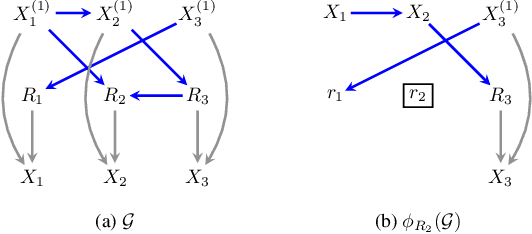
Missing data is a pervasive problem in data analyses, resulting in datasets that contain censored realizations of a target distribution. Many approaches to inference on the target distribution using censored observed data, rely on missing data models represented as a factorization with respect to a directed acyclic graph. In this paper we consider the identifiability of the target distribution within this class of models, and show that the most general identification strategies proposed so far retain a significant gap in that they fail to identify a wide class of identifiable distributions. To address this gap, we propose a new algorithm that significantly generalizes the types of manipulations used in the ID algorithm, developed in the context of causal inference, in order to obtain identification.