Assumptions and Bounds in the Instrumental Variable Model

In this note we give proofs for results relating to the Instrumental Variable (IV) model with binary response $Y$ and binary treatment $X$, but with an instrument $Z$ with $K$ states. These results were originally stated in Richardson & Robins (2014), "ACE Bounds; SEMS with Equilibrium Conditions," arXiv:1410.0470.

Can we falsify the justification of the validity of Wald confidence intervals of doubly robust functionals, without assumptions?

In this article we develop a feasible version of the assumption-lean tests in Liu et al. 20 that can falsify an analyst's justification for the validity of a reported nominal $(1 - \alpha)$ Wald confidence interval (CI) centered at a double machine learning (DML) estimator for any member of the class of doubly robust (DR) functionals studied by Rotnitzky et al. 21. The class of DR functionals is broad and of central importance in economics and biostatistics. It strictly includes both (i) the class of mean-square continuous functionals that can be written as an expectation of an affine functional of a conditional expectation studied by Chernozhukov et al. 22 and the class of functionals studied by Robins et al. 08. The present state-of-the-art estimators for DR functionals $\psi$ are DML estimators $\hat{\psi}_{1}$. The bias of $\hat{\psi}_{1}$ depends on the product of the rates at which two nuisance functions $b$ and $p$ are estimated. Most commonly an analyst justifies the validity of her Wald CIs by proving that, under her complexity-reducing assumptions, the Cauchy-Schwarz (CS) upper bound for the bias of $\hat{\psi}_{1}$ is $o (n^{- 1 / 2})$. Thus if the hypothesis $H_{0}$: the CS upper bound is $o (n^{- 1 / 2})$ is rejected by our test, we will have falsified the analyst's justification for the validity of her Wald CIs. In this work, we exhibit a valid assumption-lean falsification test of $H_{0}$, without relying on complexity-reducing assumptions on $b, p$, or their estimates $\hat{b}, \hat{p}$. Simulation experiments are conducted to demonstrate how the proposed assumption-lean test can be used in practice. An unavoidable limitation of our methodology is that no assumption-lean test of $H_{0}$, including ours, can be a consistent test. Thus failure of our test to reject is not meaningful evidence in favor of $H_{0}$.

Deep Learning Methods for Proximal Inference via Maximum Moment Restriction

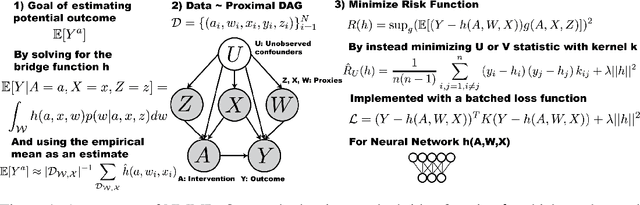
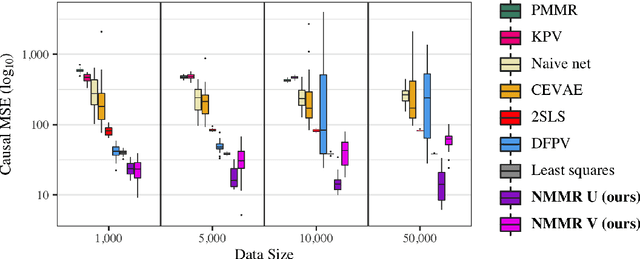
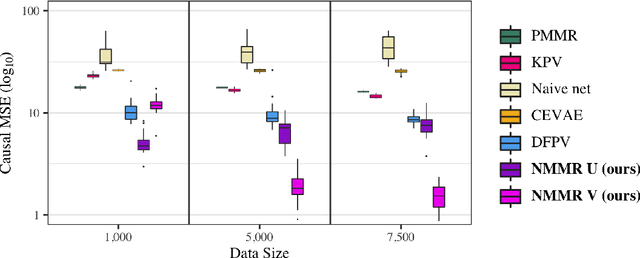
The No Unmeasured Confounding Assumption is widely used to identify causal effects in observational studies. Recent work on proximal inference has provided alternative identification results that succeed even in the presence of unobserved confounders, provided that one has measured a sufficiently rich set of proxy variables, satisfying specific structural conditions. However, proximal inference requires solving an ill-posed integral equation. Previous approaches have used a variety of machine learning techniques to estimate a solution to this integral equation, commonly referred to as the bridge function. However, prior work has often been limited by relying on pre-specified kernel functions, which are not data adaptive and struggle to scale to large datasets. In this work, we introduce a flexible and scalable method based on a deep neural network to estimate causal effects in the presence of unmeasured confounding using proximal inference. Our method achieves state of the art performance on two well-established proximal inference benchmarks. Finally, we provide theoretical consistency guarantees for our method.

Rejoinder: On nearly assumption-free tests of nominal confidence interval coverage for causal parameters estimated by machine learning

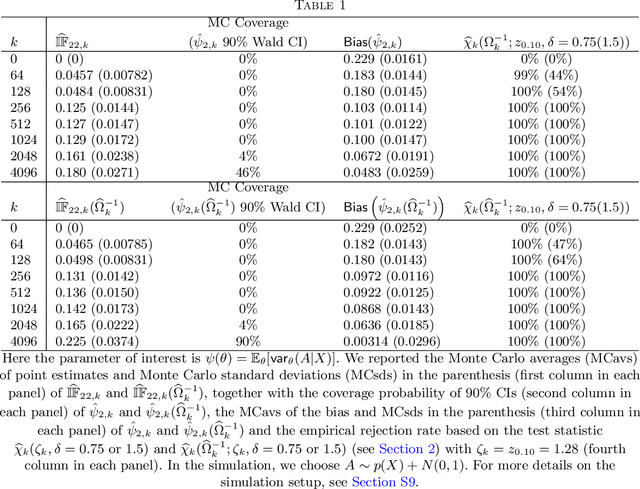
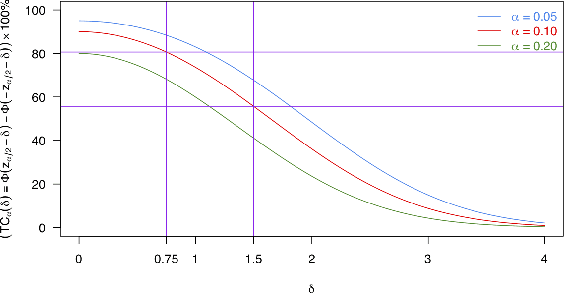
This is the rejoinder to the discussion by Kennedy, Balakrishnan and Wasserman on the paper "On nearly assumption-free tests of nominal confidence interval coverage for causal parameters estimated by machine learning" published in Statistical Science.

Identification In Missing Data Models Represented By Directed Acyclic Graphs

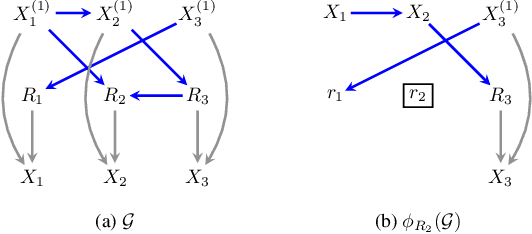
Missing data is a pervasive problem in data analyses, resulting in datasets that contain censored realizations of a target distribution. Many approaches to inference on the target distribution using censored observed data, rely on missing data models represented as a factorization with respect to a directed acyclic graph. In this paper we consider the identifiability of the target distribution within this class of models, and show that the most general identification strategies proposed so far retain a significant gap in that they fail to identify a wide class of identifiable distributions. To address this gap, we propose a new algorithm that significantly generalizes the types of manipulations used in the ID algorithm, developed in the context of causal inference, in order to obtain identification.

A unifying approach for doubly-robust $\ell_1$ regularized estimation of causal contrasts

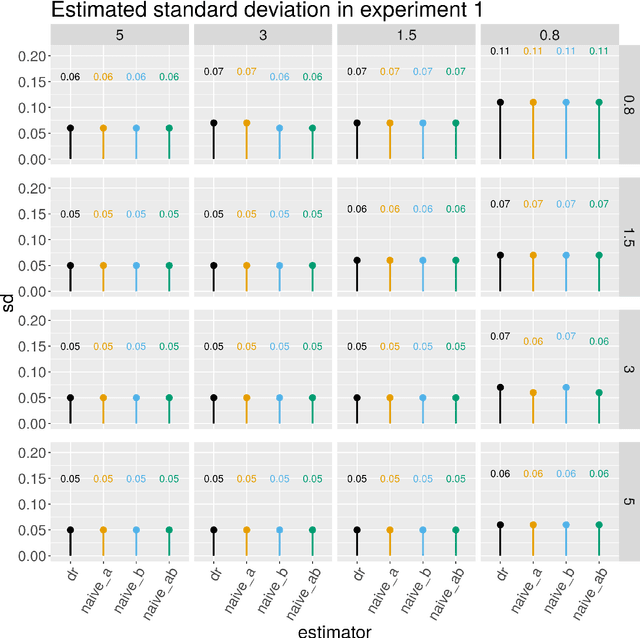
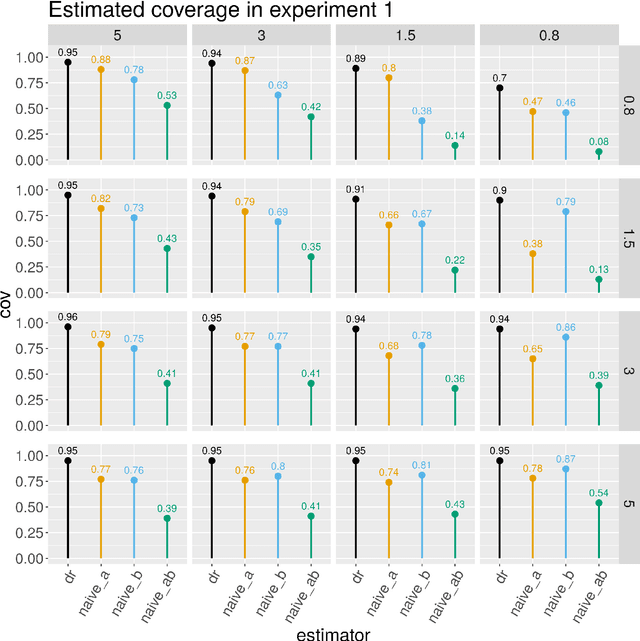
We consider inference about a scalar parameter under a non-parametric model based on a one-step estimator computed as a plug in estimator plus the empirical mean of an estimator of the parameter's influence function. We focus on a class of parameters that have influence function which depends on two infinite dimensional nuisance functions and such that the bias of the one-step estimator of the parameter of interest is the expectation of the product of the estimation errors of the two nuisance functions. Our class includes many important treatment effect contrasts of interest in causal inference and econometrics, such as ATE, ATT, an integrated causal contrast with a continuous treatment, and the mean of an outcome missing not at random. We propose estimators of the target parameter that entertain approximately sparse regression models for the nuisance functions allowing for the number of potential confounders to be even larger than the sample size. By employing sample splitting, cross-fitting and $\ell_1$-regularized regression estimators of the nuisance functions based on objective functions whose directional derivatives agree with those of the parameter's influence function, we obtain estimators of the target parameter with two desirable robustness properties: (1) they are rate doubly-robust in that they are root-n consistent and asymptotically normal when both nuisance functions follow approximately sparse models, even if one function has a very non-sparse regression coefficient, so long as the other has a sufficiently sparse regression coefficient, and (2) they are model doubly-robust in that they are root-n consistent and asymptotically normal even if one of the nuisance functions does not follow an approximately sparse model so long as the other nuisance function follows an approximately sparse model with a sufficiently sparse regression coefficient.

Influence Functions for Machine Learning: Nonparametric Estimators for Entropies, Divergences and Mutual Informations

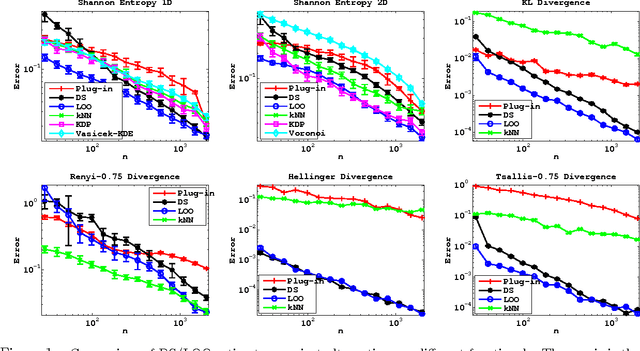
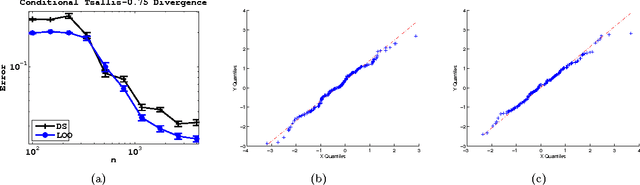
We propose and analyze estimators for statistical functionals of one or more distributions under nonparametric assumptions. Our estimators are based on the theory of influence functions, which appear in the semiparametric statistics literature. We show that estimators based either on data-splitting or a leave-one-out technique enjoy fast rates of convergence and other favorable theoretical properties. We apply this framework to derive estimators for several popular information theoretic quantities, and via empirical evaluation, show the advantage of this approach over existing estimators.

Sparse Nested Markov models with Log-linear Parameters

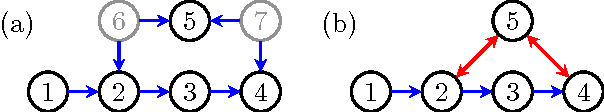
Hidden variables are ubiquitous in practical data analysis, and therefore modeling marginal densities and doing inference with the resulting models is an important problem in statistics, machine learning, and causal inference. Recently, a new type of graphical model, called the nested Markov model, was developed which captures equality constraints found in marginals of directed acyclic graph (DAG) models. Some of these constraints, such as the so called `Verma constraint', strictly generalize conditional independence. To make modeling and inference with nested Markov models practical, it is necessary to limit the number of parameters in the model, while still correctly capturing the constraints in the marginal of a DAG model. Placing such limits is similar in spirit to sparsity methods for undirected graphical models, and regression models. In this paper, we give a log-linear parameterization which allows sparse modeling with nested Markov models. We illustrate the advantages of this parameterization with a simulation study.

Probabilistic Evaluation of Sequential Plans from Causal Models with Hidden Variables

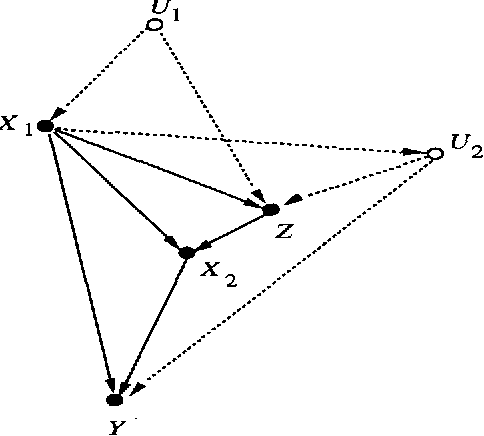
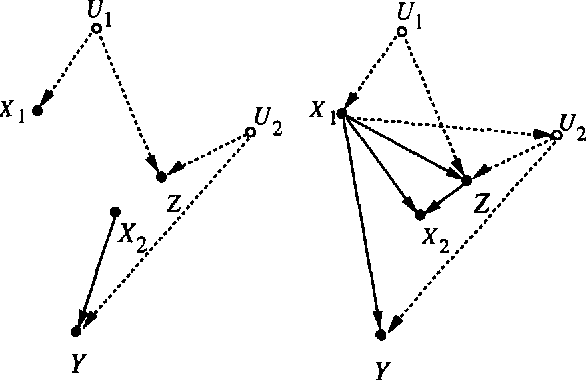
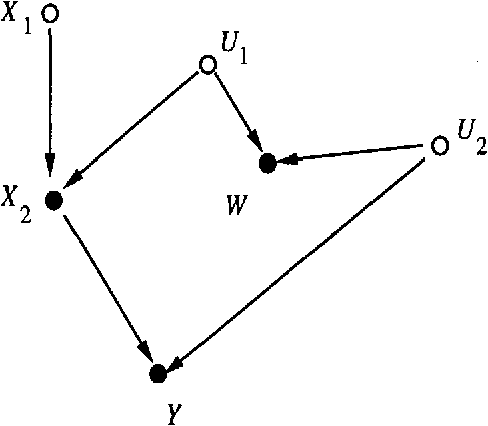
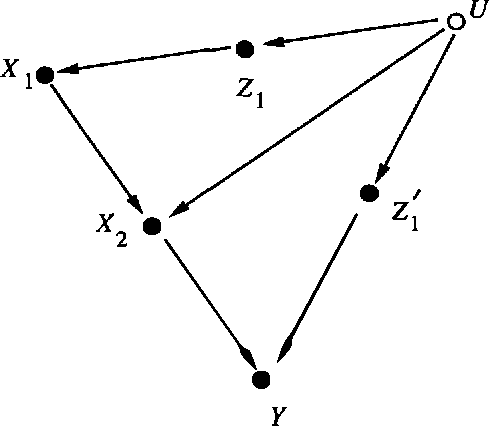
The paper concerns the probabilistic evaluation of plans in the presence of unmeasured variables, each plan consisting of several concurrent or sequential actions. We establish a graphical criterion for recognizing when the effects of a given plan can be predicted from passive observations on measured variables only. When the criterion is satisfied, a closed-form expression is provided for the probability that the plan will achieve a specified goal.