A unifying approach for doubly-robust $\ell_1$ regularized estimation of causal contrasts
Paper and Code
May 03, 2019
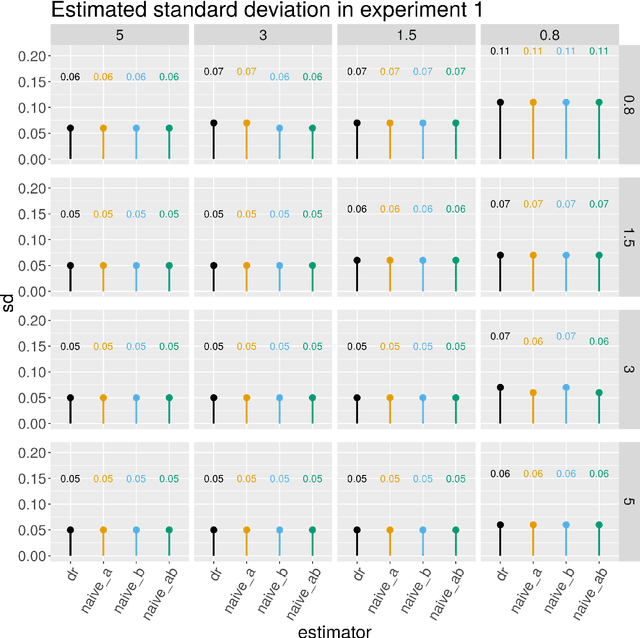
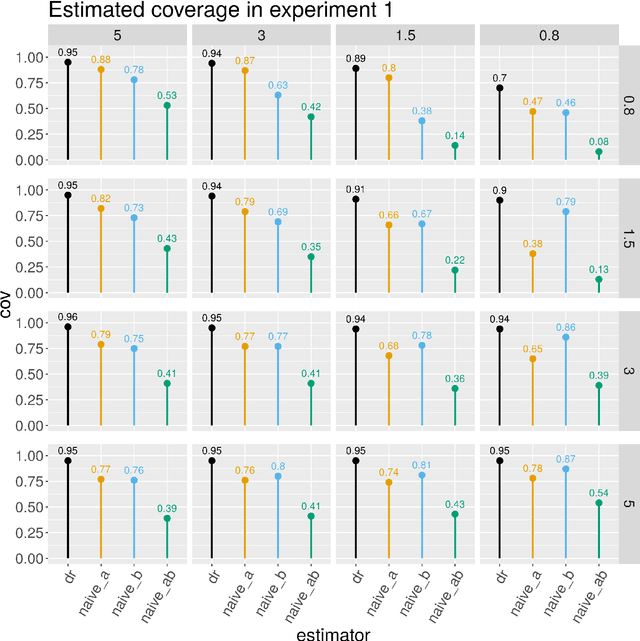

We consider inference about a scalar parameter under a non-parametric model based on a one-step estimator computed as a plug in estimator plus the empirical mean of an estimator of the parameter's influence function. We focus on a class of parameters that have influence function which depends on two infinite dimensional nuisance functions and such that the bias of the one-step estimator of the parameter of interest is the expectation of the product of the estimation errors of the two nuisance functions. Our class includes many important treatment effect contrasts of interest in causal inference and econometrics, such as ATE, ATT, an integrated causal contrast with a continuous treatment, and the mean of an outcome missing not at random. We propose estimators of the target parameter that entertain approximately sparse regression models for the nuisance functions allowing for the number of potential confounders to be even larger than the sample size. By employing sample splitting, cross-fitting and $\ell_1$-regularized regression estimators of the nuisance functions based on objective functions whose directional derivatives agree with those of the parameter's influence function, we obtain estimators of the target parameter with two desirable robustness properties: (1) they are rate doubly-robust in that they are root-n consistent and asymptotically normal when both nuisance functions follow approximately sparse models, even if one function has a very non-sparse regression coefficient, so long as the other has a sufficiently sparse regression coefficient, and (2) they are model doubly-robust in that they are root-n consistent and asymptotically normal even if one of the nuisance functions does not follow an approximately sparse model so long as the other nuisance function follows an approximately sparse model with a sufficiently sparse regression coefficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge