Deep Learning Methods for Proximal Inference via Maximum Moment Restriction
Paper and Code
May 19, 2022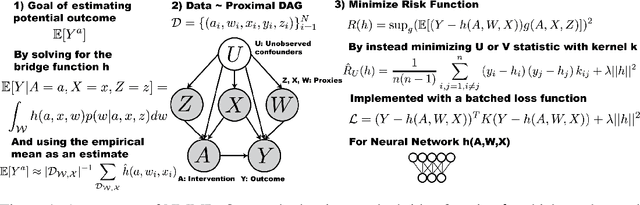

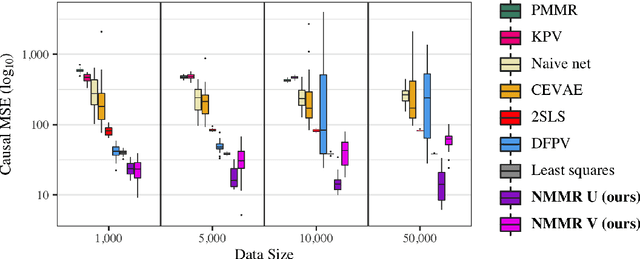
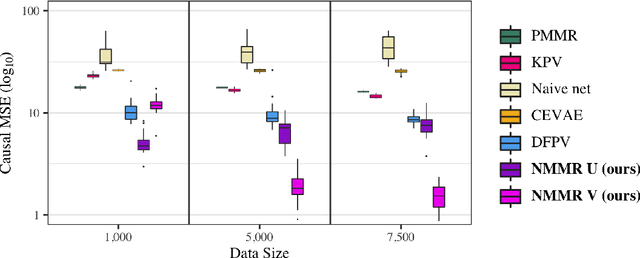
The No Unmeasured Confounding Assumption is widely used to identify causal effects in observational studies. Recent work on proximal inference has provided alternative identification results that succeed even in the presence of unobserved confounders, provided that one has measured a sufficiently rich set of proxy variables, satisfying specific structural conditions. However, proximal inference requires solving an ill-posed integral equation. Previous approaches have used a variety of machine learning techniques to estimate a solution to this integral equation, commonly referred to as the bridge function. However, prior work has often been limited by relying on pre-specified kernel functions, which are not data adaptive and struggle to scale to large datasets. In this work, we introduce a flexible and scalable method based on a deep neural network to estimate causal effects in the presence of unmeasured confounding using proximal inference. Our method achieves state of the art performance on two well-established proximal inference benchmarks. Finally, we provide theoretical consistency guarantees for our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge