DAG-aware Transformer for Causal Effect Estimation

Causal inference is a critical task across fields such as healthcare, economics, and the social sciences. While recent advances in machine learning, especially those based on the deep-learning architectures, have shown potential in estimating causal effects, existing approaches often fall short in handling complex causal structures and lack adaptability across various causal scenarios. In this paper, we present a novel transformer-based method for causal inference that overcomes these challenges. The core innovation of our model lies in its integration of causal Directed Acyclic Graphs (DAGs) directly into the attention mechanism, enabling it to accurately model the underlying causal structure. This allows for flexible estimation of both average treatment effects (ATE) and conditional average treatment effects (CATE). Extensive experiments on both synthetic and real-world datasets demonstrate that our approach surpasses existing methods in estimating causal effects across a wide range of scenarios. The flexibility and robustness of our model make it a valuable tool for researchers and practitioners tackling complex causal inference problems.

Labrador: Exploring the Limits of Masked Language Modeling for Laboratory Data

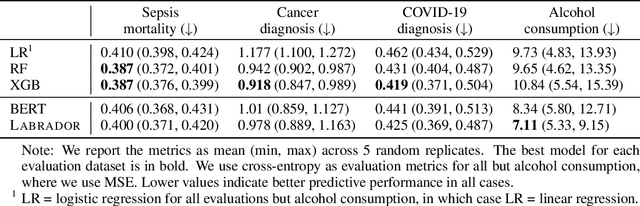
In this work we introduce Labrador, a pre-trained Transformer model for laboratory data. Labrador and BERT were pre-trained on a corpus of 100 million lab test results from electronic health records (EHRs) and evaluated on various downstream outcome prediction tasks. Both models demonstrate mastery of the pre-training task but neither consistently outperform XGBoost on downstream supervised tasks. Our ablation studies reveal that transfer learning shows limited effectiveness for BERT and achieves marginal success with Labrador. We explore the reasons for the failure of transfer learning and suggest that the data generating process underlying each patient cannot be characterized sufficiently using labs alone, among other factors. We encourage future work to focus on joint modeling of multiple EHR data categories and to include tree-based baselines in their evaluations.

Deep Learning Methods for Proximal Inference via Maximum Moment Restriction

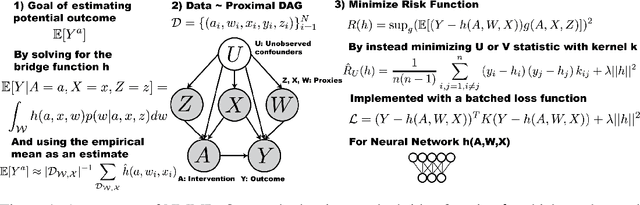
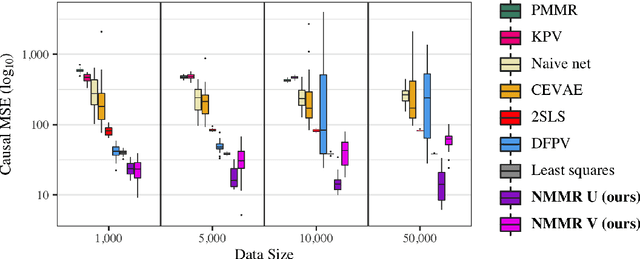
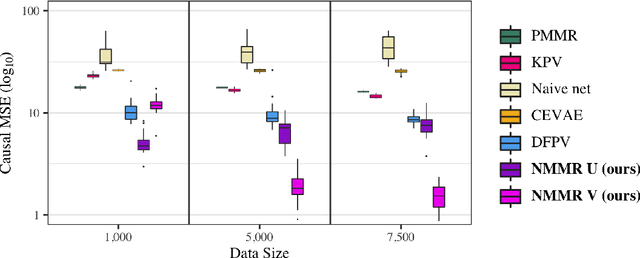
The No Unmeasured Confounding Assumption is widely used to identify causal effects in observational studies. Recent work on proximal inference has provided alternative identification results that succeed even in the presence of unobserved confounders, provided that one has measured a sufficiently rich set of proxy variables, satisfying specific structural conditions. However, proximal inference requires solving an ill-posed integral equation. Previous approaches have used a variety of machine learning techniques to estimate a solution to this integral equation, commonly referred to as the bridge function. However, prior work has often been limited by relying on pre-specified kernel functions, which are not data adaptive and struggle to scale to large datasets. In this work, we introduce a flexible and scalable method based on a deep neural network to estimate causal effects in the presence of unmeasured confounding using proximal inference. Our method achieves state of the art performance on two well-established proximal inference benchmarks. Finally, we provide theoretical consistency guarantees for our method.