Testing Generalizability in Causal Inference

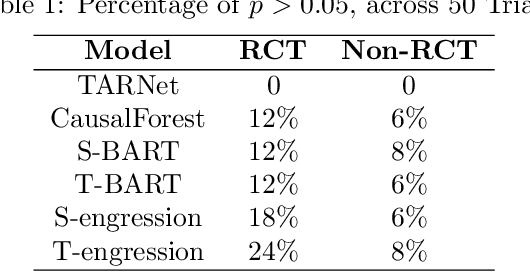
Ensuring robust model performance across diverse real-world scenarios requires addressing both transportability across domains with covariate shifts and extrapolation beyond observed data ranges. However, there is no formal procedure for statistically evaluating generalizability in machine learning algorithms, particularly in causal inference. Existing methods often rely on arbitrary metrics like AUC or MSE and focus predominantly on toy datasets, providing limited insights into real-world applicability. To address this gap, we propose a systematic and quantitative framework for evaluating model generalizability under covariate distribution shifts, specifically within causal inference settings. Our approach leverages the frugal parameterization, allowing for flexible simulations from fully and semi-synthetic benchmarks, offering comprehensive evaluations for both mean and distributional regression methods. By basing simulations on real data, our method ensures more realistic evaluations, which is often missing in current work relying on simplified datasets. Furthermore, using simulations and statistical testing, our framework is robust and avoids over-reliance on conventional metrics. Grounded in real-world data, it provides realistic insights into model performance, bridging the gap between synthetic evaluations and practical applications.

Marginal Causal Flows for Validation and Inference

Investigating the marginal causal effect of an intervention on an outcome from complex data remains challenging due to the inflexibility of employed models and the lack of complexity in causal benchmark datasets, which often fail to reproduce intricate real-world data patterns. In this paper we introduce Frugal Flows, a novel likelihood-based machine learning model that uses normalising flows to flexibly learn the data-generating process, while also directly inferring the marginal causal quantities from observational data. We propose that these models are exceptionally well suited for generating synthetic data to validate causal methods. They can create synthetic datasets that closely resemble the empirical dataset, while automatically and exactly satisfying a user-defined average treatment effect. To our knowledge, Frugal Flows are the first generative model to both learn flexible data representations and also exactly parameterise quantities such as the average treatment effect and the degree of unobserved confounding. We demonstrate the above with experiments on both simulated and real-world datasets.

Results on Counterfactual Invariance

In this paper we provide a theoretical analysis of counterfactual invariance. We present a variety of existing definitions, study how they relate to each other and what their graphical implications are. We then turn to the current major question surrounding counterfactual invariance, how does it relate to conditional independence? We show that whilst counterfactual invariance implies conditional independence, conditional independence does not give any implications about the degree or likelihood of satisfying counterfactual invariance. Furthermore, we show that for discrete causal models counterfactually invariant functions are often constrained to be functions of particular variables, or even constant.

PWSHAP: A Path-Wise Explanation Model for Targeted Variables

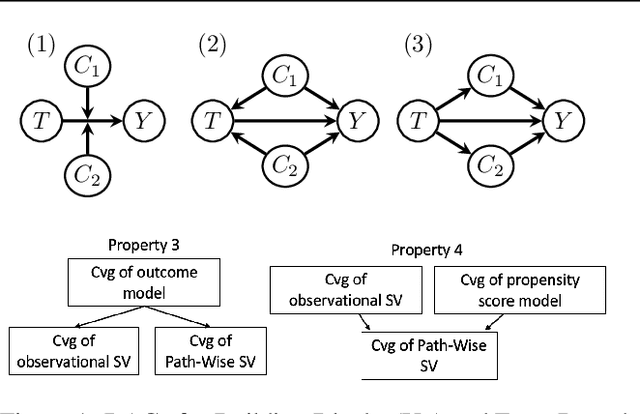
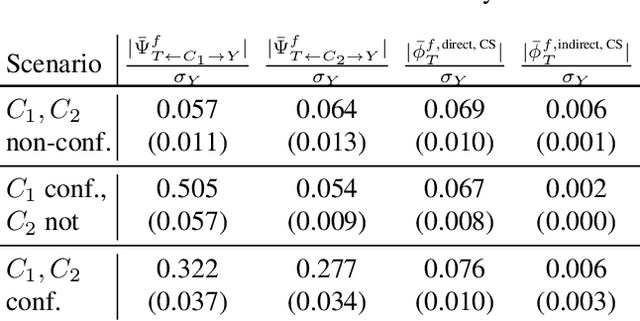
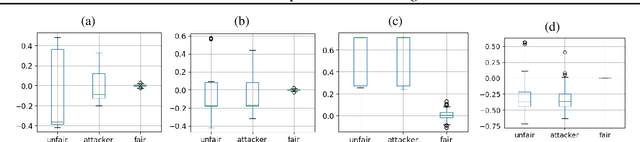
Predictive black-box models can exhibit high accuracy but their opaque nature hinders their uptake in safety-critical deployment environments. Explanation methods (XAI) can provide confidence for decision-making through increased transparency. However, existing XAI methods are not tailored towards models in sensitive domains where one predictor is of special interest, such as a treatment effect in a clinical model, or ethnicity in policy models. We introduce Path-Wise Shapley effects (PWSHAP), a framework for assessing the targeted effect of a binary (e.g.~treatment) variable from a complex outcome model. Our approach augments the predictive model with a user-defined directed acyclic graph (DAG). The method then uses the graph alongside on-manifold Shapley values to identify effects along causal pathways whilst maintaining robustness to adversarial attacks. We establish error bounds for the identified path-wise Shapley effects and for Shapley values. We show PWSHAP can perform local bias and mediation analyses with faithfulness to the model. Further, if the targeted variable is randomised we can quantify local effect modification. We demonstrate the resolution, interpretability, and true locality of our approach on examples and a real-world experiment.

Doubly Robust Kernel Statistics for Testing Distributional Treatment Effects Even Under One Sided Overlap

As causal inference becomes more widespread the importance of having good tools to test for causal effects increases. In this work we focus on the problem of testing for causal effects that manifest in a difference in distribution for treatment and control. We build on work applying kernel methods to causality, considering the previously introduced Counterfactual Mean Embedding framework (\textsc{CfME}). We improve on this by proposing the \emph{Doubly Robust Counterfactual Mean Embedding} (\textsc{DR-CfME}), which has better theoretical properties than its predecessor by leveraging semiparametric theory. This leads us to propose new kernel based test statistics for distributional effects which are based upon doubly robust estimators of treatment effects. We propose two test statistics, one which is a direct improvement on previous work and one which can be applied even when the support of the treatment arm is a subset of that of the control arm. We demonstrate the validity of our methods on simulated and real-world data, as well as giving an application in off-policy evaluation.

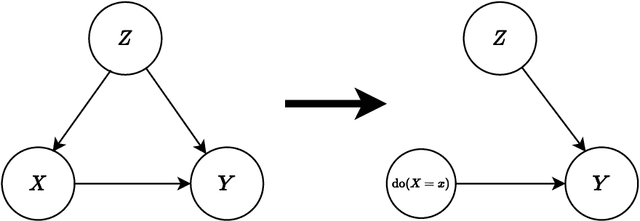
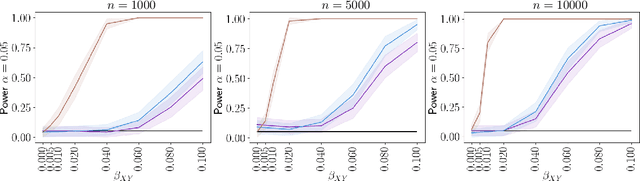
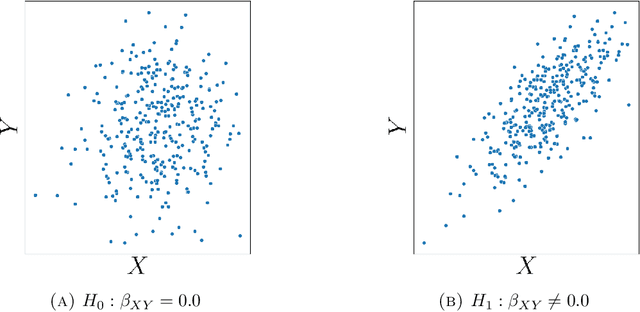
A Kernel Test for Causal Association via Noise Contrastive Backdoor Adjustment

Causal inference grows increasingly complex as the number of confounders increases. Given treatments $X$, confounders $Z$ and outcomes $Y$, we develop a non-parametric method to test the \textit{do-null} hypothesis $H_0:\; p(y|\text{\it do}(X=x))=p(y)$ against the general alternative. Building on the Hilbert Schmidt Independence Criterion (HSIC) for marginal independence testing, we propose backdoor-HSIC (bd-HSIC) and demonstrate that it is calibrated and has power for both binary and continuous treatments under a large number of confounders. Additionally, we establish convergence properties of the estimators of covariance operators used in bd-HSIC. We investigate the advantages and disadvantages of bd-HSIC against parametric tests as well as the importance of using the do-null testing in contrast to marginal independence testing or conditional independence testing. A complete implementation can be found at \hyperlink{https://github.com/MrHuff/kgformula}{\texttt{https://github.com/MrHuff/kgformula}}.

Distributional Equivalence and Structure Learning for Bow-free Acyclic Path Diagrams

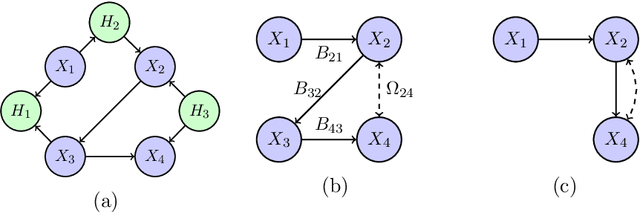
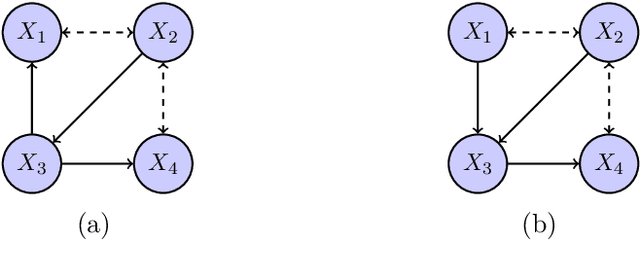
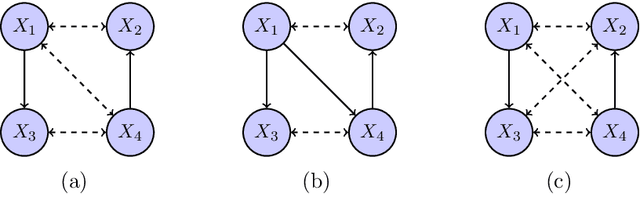
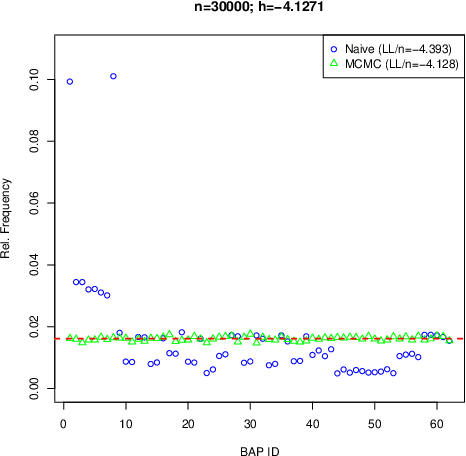
We consider the problem of structure learning for bow-free acyclic path diagrams (BAPs). BAPs can be viewed as a generalization of linear Gaussian DAG models that allow for certain hidden variables. We present a first method for this problem using a greedy score-based search algorithm. We also prove some necessary and some sufficient conditions for distributional equivalence of BAPs which are used in an algorithmic ap- proach to compute (nearly) equivalent model structures. This allows us to infer lower bounds of causal effects. We also present applications to real and simulated datasets using our publicly available R-package.

Margins of discrete Bayesian networks

Bayesian network models with latent variables are widely used in statistics and machine learning. In this paper we provide a complete algebraic characterization of Bayesian network models with latent variables when the observed variables are discrete and no assumption is made about the state-space of the latent variables. We show that it is algebraically equivalent to the so-called nested Markov model, meaning that the two are the same up to inequality constraints on the joint probabilities. In particular these two models have the same dimension. The nested Markov model is therefore the best possible description of the latent variable model that avoids consideration of inequalities, which are extremely complicated in general. A consequence of this is that the constraint finding algorithm of Tian and Pearl (UAI 2002, pp519-527) is complete for finding equality constraints. Latent variable models suffer from difficulties of unidentifiable parameters and non-regular asymptotics; in contrast the nested Markov model is fully identifiable, represents a curved exponential family of known dimension, and can easily be fitted using an explicit parameterization.

Sparse Nested Markov models with Log-linear Parameters

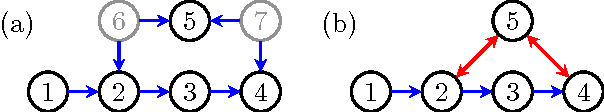
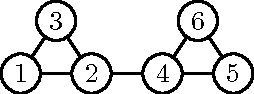
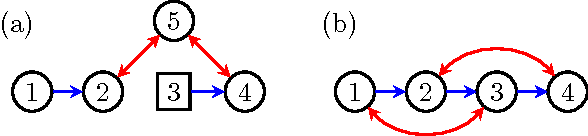
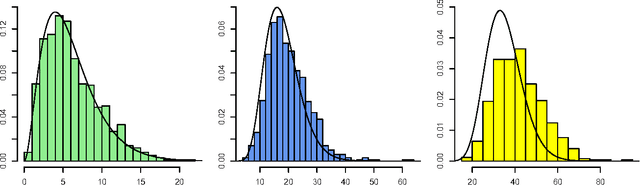
Hidden variables are ubiquitous in practical data analysis, and therefore modeling marginal densities and doing inference with the resulting models is an important problem in statistics, machine learning, and causal inference. Recently, a new type of graphical model, called the nested Markov model, was developed which captures equality constraints found in marginals of directed acyclic graph (DAG) models. Some of these constraints, such as the so called `Verma constraint', strictly generalize conditional independence. To make modeling and inference with nested Markov models practical, it is necessary to limit the number of parameters in the model, while still correctly capturing the constraints in the marginal of a DAG model. Placing such limits is similar in spirit to sparsity methods for undirected graphical models, and regression models. In this paper, we give a log-linear parameterization which allows sparse modeling with nested Markov models. We illustrate the advantages of this parameterization with a simulation study.

Maximum likelihood fitting of acyclic directed mixed graphs to binary data

Acyclic directed mixed graphs, also known as semi-Markov models represent the conditional independence structure induced on an observed margin by a DAG model with latent variables. In this paper we present the first method for fitting these models to binary data using maximum likelihood estimation.