Domain Generalization and Adaptation in Intensive Care with Anchor Regression

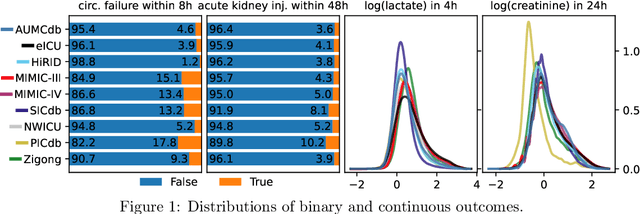
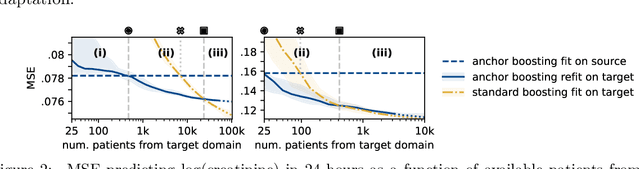
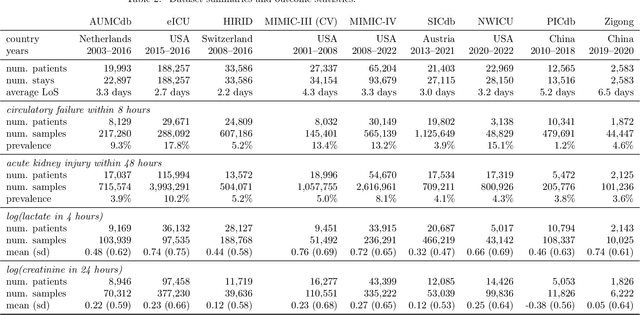
The performance of predictive models in clinical settings often degrades when deployed in new hospitals due to distribution shifts. This paper presents a large-scale study of causality-inspired domain generalization on heterogeneous multi-center intensive care unit (ICU) data. We apply anchor regression and introduce anchor boosting, a novel, tree-based nonlinear extension, to a large dataset comprising 400,000 patients from nine distinct ICU databases. The anchor regularization consistently improves out-of-distribution performance, particularly for the most dissimilar target domains. The methods appear robust to violations of theoretical assumptions, such as anchor exogeneity. Furthermore, we propose a novel conceptual framework to quantify the utility of large external data datasets. By evaluating performance as a function of available target-domain data, we identify three regimes: (i) a domain generalization regime, where only the external model should be used, (ii) a domain adaptation regime, where refitting the external model is optimal, and (iii) a data-rich regime, where external data provides no additional value.

Causality-Inspired Robustness for Nonlinear Models via Representation Learning

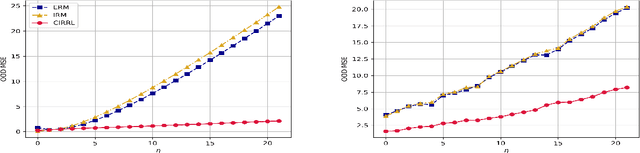
Distributional robustness is a central goal of prediction algorithms due to the prevalent distribution shifts in real-world data. The prediction model aims to minimize the worst-case risk among a class of distributions, a.k.a., an uncertainty set. Causality provides a modeling framework with a rigorous robustness guarantee in the above sense, where the uncertainty set is data-driven rather than pre-specified as in traditional distributional robustness optimization. However, current causality-inspired robustness methods possess finite-radius robustness guarantees only in the linear settings, where the causal relationships among the covariates and the response are linear. In this work, we propose a nonlinear method under a causal framework by incorporating recent developments in identifiable representation learning and establish a distributional robustness guarantee. To our best knowledge, this is the first causality-inspired robustness method with such a finite-radius robustness guarantee in nonlinear settings. Empirical validation of the theoretical findings is conducted on both synthetic data and real-world single-cell data, also illustrating that finite-radius robustness is crucial.

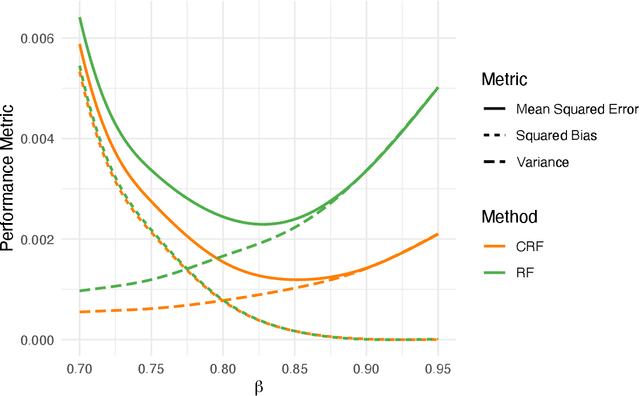
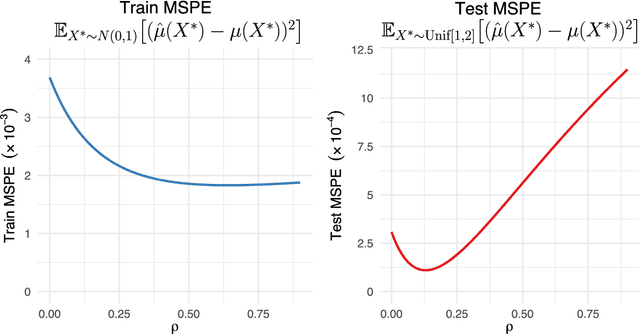
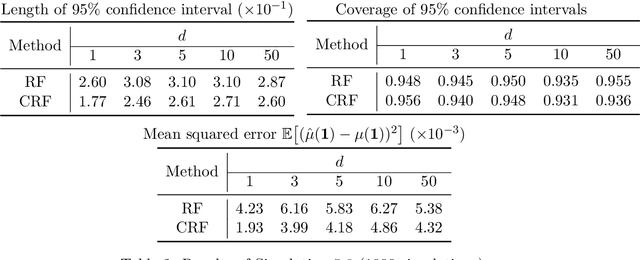
Clustered random forests with correlated data for optimal estimation and inference under potential covariate shift

We develop Clustered Random Forests, a random forests algorithm for clustered data, arising from independent groups that exhibit within-cluster dependence. The leaf-wise predictions for each decision tree making up clustered random forests takes the form of a weighted least squares estimator, which leverage correlations between observations for improved prediction accuracy. Clustered random forests are shown for certain tree splitting criteria to be minimax rate optimal for pointwise conditional mean estimation, while being computationally competitive with standard random forests. Further, we observe that the optimality of a clustered random forest, with regards to how (population level) optimal weights are chosen within this framework i.e. those that minimise mean squared prediction error, vary under covariate distribution shift. In light of this, we advocate weight estimation to be determined by a user-chosen covariate distribution with respect to which optimal prediction or inference is desired. This highlights a key difference in behaviour, between correlated and independent data, with regards to nonparametric conditional mean estimation under covariate shift. We demonstrate our theoretical findings numerically in a number of simulated and real-world settings.

Causal Invariance Learning via Efficient Optimization of a Nonconvex Objective

Data from multiple environments offer valuable opportunities to uncover causal relationships among variables. Leveraging the assumption that the causal outcome model remains invariant across heterogeneous environments, state-of-the-art methods attempt to identify causal outcome models by learning invariant prediction models and rely on exhaustive searches over all (exponentially many) covariate subsets. These approaches present two major challenges: 1) determining the conditions under which the invariant prediction model aligns with the causal outcome model, and 2) devising computationally efficient causal discovery algorithms that scale polynomially, instead of exponentially, with the number of covariates. To address both challenges, we focus on the additive intervention regime and propose nearly necessary and sufficient conditions for ensuring that the invariant prediction model matches the causal outcome model. Exploiting the essentially necessary identifiability conditions, we introduce Negative Weight Distributionally Robust Optimization (NegDRO), a nonconvex continuous minimax optimization whose global optimizer recovers the causal outcome model. Unlike standard group DRO problems that maximize over the simplex, NegDRO allows negative weights on environment losses, which break the convexity. Despite its nonconvexity, we demonstrate that a standard gradient method converges to the causal outcome model, and we establish the convergence rate with respect to the sample size and the number of iterations. Our algorithm avoids exhaustive search, making it scalable especially when the number of covariates is large. The numerical results further validate the efficiency of the proposed method.

Causality Pursuit from Heterogeneous Environments via Neural Adversarial Invariance Learning

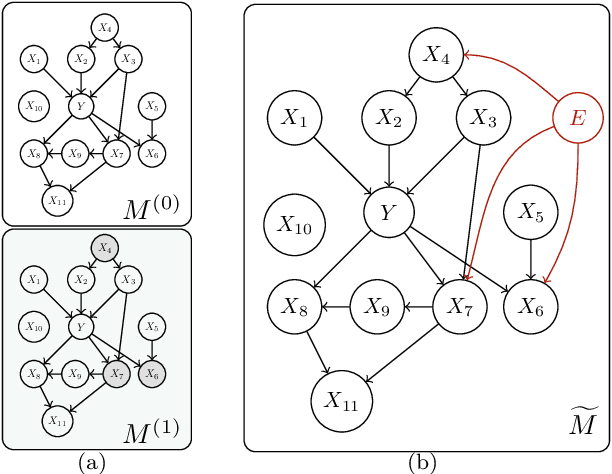
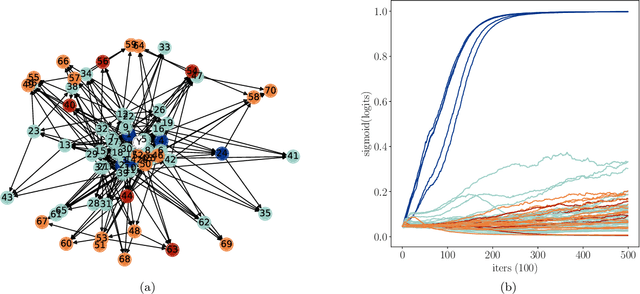
Statistics suffers from a fundamental problem, "the curse of endogeneity" -- the regression function, or more broadly the prediction risk minimizer with infinite data, may not be the target we wish to pursue. This is because when complex data are collected from multiple sources, the biases deviated from the interested (causal) association inherited in individuals or sub-populations are not expected to be canceled. Traditional remedies are of hindsight and restrictive in being tailored to prior knowledge like untestable cause-effect structures, resulting in methods that risk model misspecification and lack scalable applicability. This paper seeks to offer a purely data-driven and universally applicable method that only uses the heterogeneity of the biases in the data rather than following pre-offered commandments. Such an idea is formulated as a nonparametric invariance pursuit problem, whose goal is to unveil the invariant conditional expectation $m^\star(x)\equiv \mathbb{E}[Y^{(e)}|X_{S^\star}^{(e)}=x_{S^\star}]$ with unknown important variable set $S^\star$ across heterogeneous environments $e\in \mathcal{E}$. Under the structural causal model framework, $m^\star$ can be interpreted as certain data-driven causality in general. The paper contributes to proposing a novel framework, called Focused Adversarial Invariance Regularization (FAIR), formulated as a single minimax optimization program that can solve the general invariance pursuit problem. As illustrated by the unified non-asymptotic analysis, our adversarial estimation framework can attain provable sample-efficient estimation akin to standard regression under a minimal identification condition for various tasks and models. As an application, the FAIR-NN estimator realized by two Neural Network classes is highlighted as the first approach to attain statistically efficient estimation in general nonparametric invariance learning.

The Causal Chambers: Real Physical Systems as a Testbed for AI Methodology

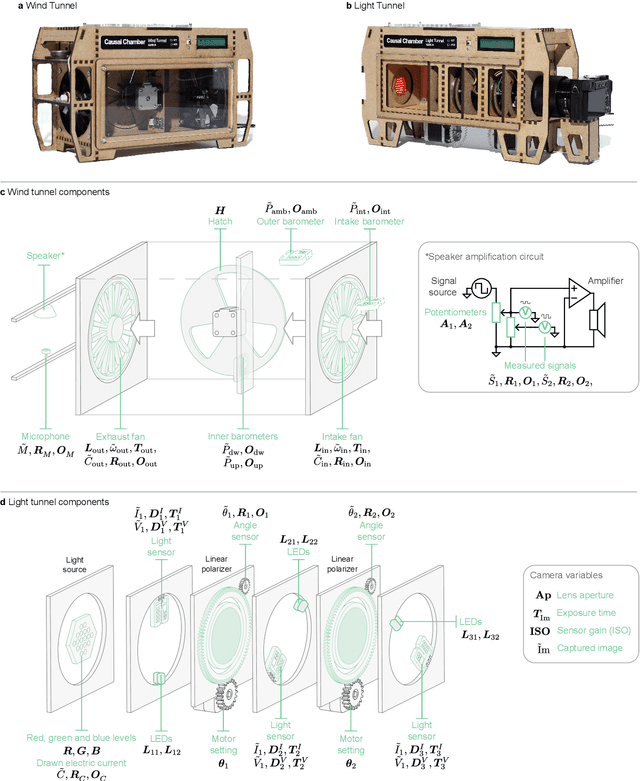
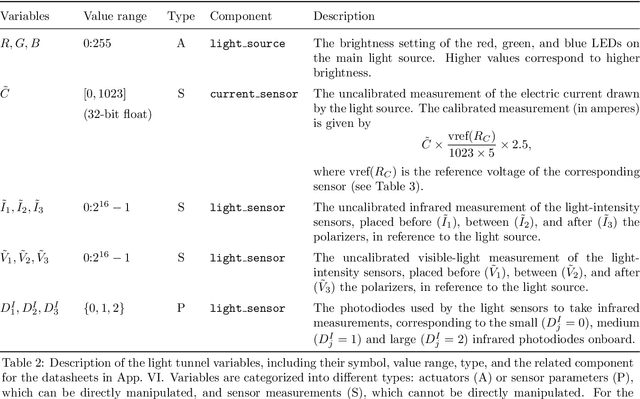
In some fields of AI, machine learning and statistics, the validation of new methods and algorithms is often hindered by the scarcity of suitable real-world datasets. Researchers must often turn to simulated data, which yields limited information about the applicability of the proposed methods to real problems. As a step forward, we have constructed two devices that allow us to quickly and inexpensively produce large datasets from non-trivial but well-understood physical systems. The devices, which we call causal chambers, are computer-controlled laboratories that allow us to manipulate and measure an array of variables from these physical systems, providing a rich testbed for algorithms from a variety of fields. We illustrate potential applications through a series of case studies in fields such as causal discovery, out-of-distribution generalization, change point detection, independent component analysis, and symbolic regression. For applications to causal inference, the chambers allow us to carefully perform interventions. We also provide and empirically validate a causal model of each chamber, which can be used as ground truth for different tasks. All hardware and software is made open source, and the datasets are publicly available at causalchamber.org or through the Python package causalchamber.

Extrapolation-Aware Nonparametric Statistical Inference

We define extrapolation as any type of statistical inference on a conditional function (e.g., a conditional expectation or conditional quantile) evaluated outside of the support of the conditioning variable. This type of extrapolation occurs in many data analysis applications and can invalidate the resulting conclusions if not taken into account. While extrapolating is straightforward in parametric models, it becomes challenging in nonparametric models. In this work, we extend the nonparametric statistical model to explicitly allow for extrapolation and introduce a class of extrapolation assumptions that can be combined with existing inference techniques to draw extrapolation-aware conclusions. The proposed class of extrapolation assumptions stipulate that the conditional function attains its minimal and maximal directional derivative, in each direction, within the observed support. We illustrate how the framework applies to several statistical applications including prediction and uncertainty quantification. We furthermore propose a consistent estimation procedure that can be used to adjust existing nonparametric estimates to account for extrapolation by providing lower and upper extrapolation bounds. The procedure is empirically evaluated on both simulated and real-world data.

Assessing the overall and partial causal well-specification of nonlinear additive noise models

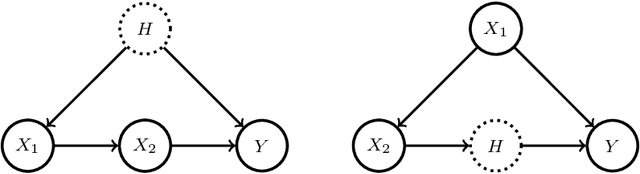
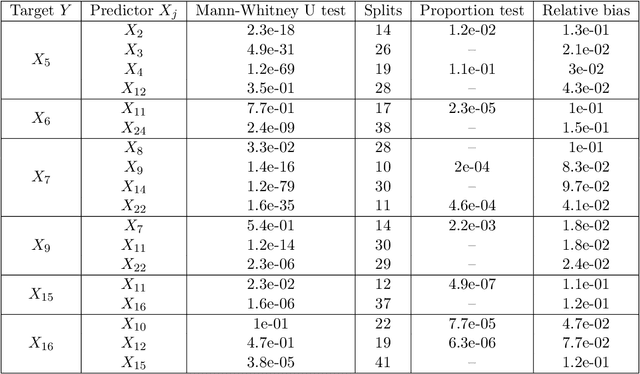
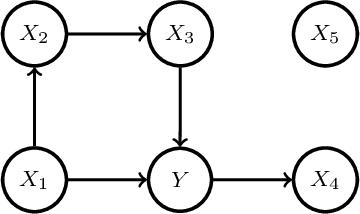
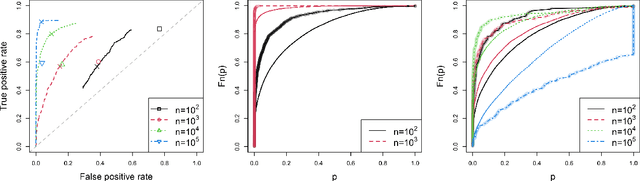
We propose a method to detect model misspecifications in nonlinear causal additive and potentially heteroscedastic noise models. We aim to identify predictor variables for which we can infer the causal effect even in cases of such misspecification. We develop a general framework based on knowledge of the multivariate observational data distribution and we then propose an algorithm for finite sample data, discuss its asymptotic properties, and illustrate its performance on simulated and real data.

Invariant Probabilistic Prediction

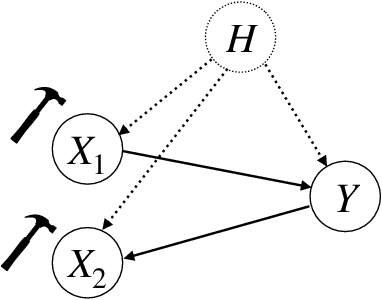
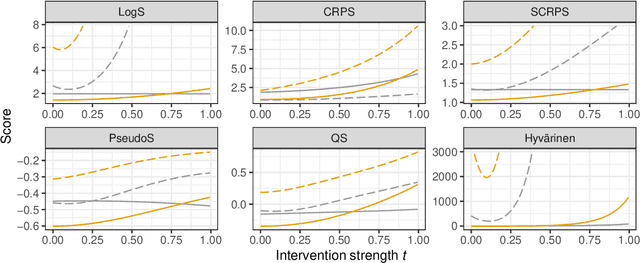
In recent years, there has been a growing interest in statistical methods that exhibit robust performance under distribution changes between training and test data. While most of the related research focuses on point predictions with the squared error loss, this article turns the focus towards probabilistic predictions, which aim to comprehensively quantify the uncertainty of an outcome variable given covariates. Within a causality-inspired framework, we investigate the invariance and robustness of probabilistic predictions with respect to proper scoring rules. We show that arbitrary distribution shifts do not, in general, admit invariant and robust probabilistic predictions, in contrast to the setting of point prediction. We illustrate how to choose evaluation metrics and restrict the class of distribution shifts to allow for identifiability and invariance in the prototypical Gaussian heteroscedastic linear model. Motivated by these findings, we propose a method to yield invariant probabilistic predictions, called IPP, and study the consistency of the underlying parameters. Finally, we demonstrate the empirical performance of our proposed procedure on simulated as well as on single-cell data.

Distributionally Robust Machine Learning with Multi-source Data

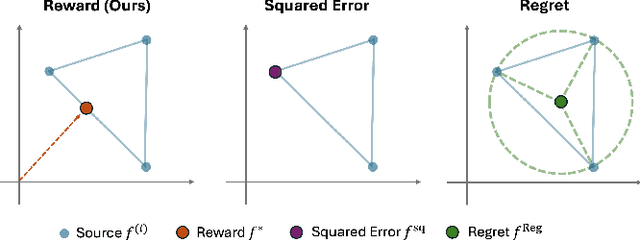
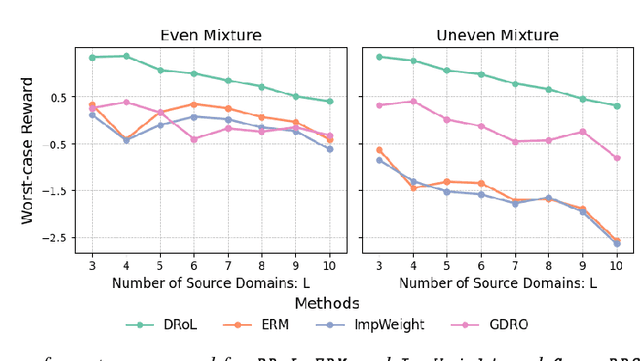
Classical machine learning methods may lead to poor prediction performance when the target distribution differs from the source populations. This paper utilizes data from multiple sources and introduces a group distributionally robust prediction model defined to optimize an adversarial reward about explained variance with respect to a class of target distributions. Compared to classical empirical risk minimization, the proposed robust prediction model improves the prediction accuracy for target populations with distribution shifts. We show that our group distributionally robust prediction model is a weighted average of the source populations' conditional outcome models. We leverage this key identification result to robustify arbitrary machine learning algorithms, including, for example, random forests and neural networks. We devise a novel bias-corrected estimator to estimate the optimal aggregation weight for general machine-learning algorithms and demonstrate its improvement in the convergence rate. Our proposal can be seen as a distributionally robust federated learning approach that is computationally efficient and easy to implement using arbitrary machine learning base algorithms, satisfies some privacy constraints, and has a nice interpretation of different sources' importance for predicting a given target covariate distribution. We demonstrate the performance of our proposed group distributionally robust method on simulated and real data with random forests and neural networks as base-learning algorithms.