Causality Pursuit from Heterogeneous Environments via Neural Adversarial Invariance Learning

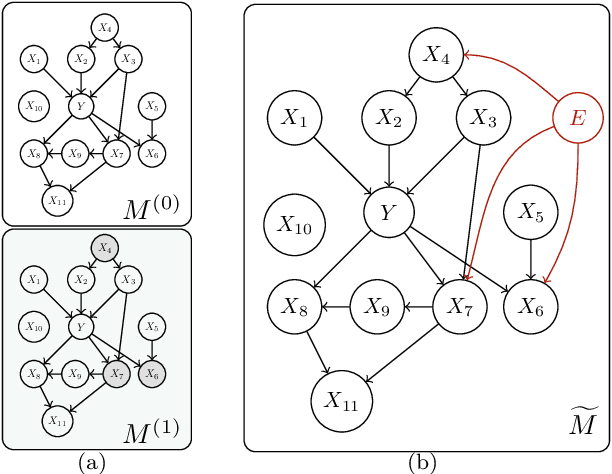
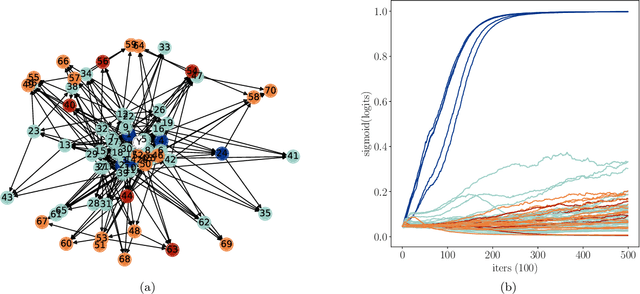
Statistics suffers from a fundamental problem, "the curse of endogeneity" -- the regression function, or more broadly the prediction risk minimizer with infinite data, may not be the target we wish to pursue. This is because when complex data are collected from multiple sources, the biases deviated from the interested (causal) association inherited in individuals or sub-populations are not expected to be canceled. Traditional remedies are of hindsight and restrictive in being tailored to prior knowledge like untestable cause-effect structures, resulting in methods that risk model misspecification and lack scalable applicability. This paper seeks to offer a purely data-driven and universally applicable method that only uses the heterogeneity of the biases in the data rather than following pre-offered commandments. Such an idea is formulated as a nonparametric invariance pursuit problem, whose goal is to unveil the invariant conditional expectation $m^\star(x)\equiv \mathbb{E}[Y^{(e)}|X_{S^\star}^{(e)}=x_{S^\star}]$ with unknown important variable set $S^\star$ across heterogeneous environments $e\in \mathcal{E}$. Under the structural causal model framework, $m^\star$ can be interpreted as certain data-driven causality in general. The paper contributes to proposing a novel framework, called Focused Adversarial Invariance Regularization (FAIR), formulated as a single minimax optimization program that can solve the general invariance pursuit problem. As illustrated by the unified non-asymptotic analysis, our adversarial estimation framework can attain provable sample-efficient estimation akin to standard regression under a minimal identification condition for various tasks and models. As an application, the FAIR-NN estimator realized by two Neural Network classes is highlighted as the first approach to attain statistically efficient estimation in general nonparametric invariance learning.