Covariates-Adjusted Mixed-Membership Estimation: A Novel Network Model with Optimal Guarantees

This paper addresses the problem of mixed-membership estimation in networks, where the goal is to efficiently estimate the latent mixed-membership structure from the observed network. Recognizing the widespread availability and valuable information carried by node covariates, we propose a novel network model that incorporates both community information, as represented by the Degree-Corrected Mixed Membership (DCMM) model, and node covariate similarities to determine connections. We investigate the regularized maximum likelihood estimation (MLE) for this model and demonstrate that our approach achieves optimal estimation accuracy for both the similarity matrix and the mixed-membership, in terms of both the Frobenius norm and the entrywise loss. Since directly analyzing the original convex optimization problem is intractable, we employ nonconvex optimization to facilitate the analysis. A key contribution of our work is identifying a crucial assumption that bridges the gap between convex and nonconvex solutions, enabling the transfer of statistical guarantees from the nonconvex approach to its convex counterpart. Importantly, our analysis extends beyond the MLE loss and the mean squared error (MSE) used in matrix completion problems, generalizing to all the convex loss functions. Consequently, our analysis techniques extend to a broader set of applications, including ranking problems based on pairwise comparisons. Finally, simulation experiments validate our theoretical findings, and real-world data analyses confirm the practical relevance of our model.

Transformers versus the EM Algorithm in Multi-class Clustering

LLMs demonstrate significant inference capacities in complicated machine learning tasks, using the Transformer model as its backbone. Motivated by the limited understanding of such models on the unsupervised learning problems, we study the learning guarantees of Transformers in performing multi-class clustering of the Gaussian Mixture Models. We develop a theory drawing strong connections between the Softmax Attention layers and the workflow of the EM algorithm on clustering the mixture of Gaussians. Our theory provides approximation bounds for the Expectation and Maximization steps by proving the universal approximation abilities of multivariate mappings by Softmax functions. In addition to the approximation guarantees, we also show that with a sufficient number of pre-training samples and an initialization, Transformers can achieve the minimax optimal rate for the problem considered. Our extensive simulations empirically verified our theory by revealing the strong learning capacities of Transformers even beyond the assumptions in the theory, shedding light on the powerful inference capacities of LLMs.

Transformers and Their Roles as Time Series Foundation Models

We give a comprehensive analysis of transformers as time series foundation models, focusing on their approximation and generalization capabilities. First, we demonstrate that there exist transformers that fit an autoregressive model on input univariate time series via gradient descent. We then analyze MOIRAI, a multivariate time series foundation model capable of handling an arbitrary number of covariates. We prove that it is capable of automatically fitting autoregressive models with an arbitrary number of covariates, offering insights into its design and empirical success. For generalization, we establish bounds for pretraining when the data satisfies Dobrushin's condition. Experiments support our theoretical findings, highlighting the efficacy of transformers as time series foundation models.

Fundamental Computational Limits in Pursuing Invariant Causal Prediction and Invariance-Guided Regularization

Pursuing invariant prediction from heterogeneous environments opens the door to learning causality in a purely data-driven way and has several applications in causal discovery and robust transfer learning. However, existing methods such as ICP [Peters et al., 2016] and EILLS [Fan et al., 2024] that can attain sample-efficient estimation are based on exponential time algorithms. In this paper, we show that such a problem is intrinsically hard in computation: the decision problem, testing whether a non-trivial prediction-invariant solution exists across two environments, is NP-hard even for the linear causal relationship. In the world where P$\neq$NP, our results imply that the estimation error rate can be arbitrarily slow using any computationally efficient algorithm. This suggests that pursuing causality is fundamentally harder than detecting associations when no prior assumption is pre-offered. Given there is almost no hope of computational improvement under the worst case, this paper proposes a method capable of attaining both computationally and statistically efficient estimation under additional conditions. Furthermore, our estimator is a distributionally robust estimator with an ellipse-shaped uncertain set where more uncertainty is placed on spurious directions than invariant directions, resulting in a smooth interpolation between the most predictive solution and the causal solution by varying the invariance hyper-parameter. Non-asymptotic results and empirical applications support the claim.

Deep Transfer $Q$-Learning for Offline Non-Stationary Reinforcement Learning

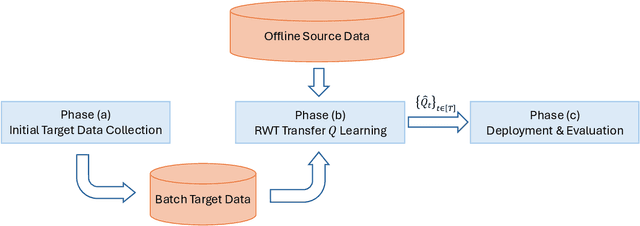
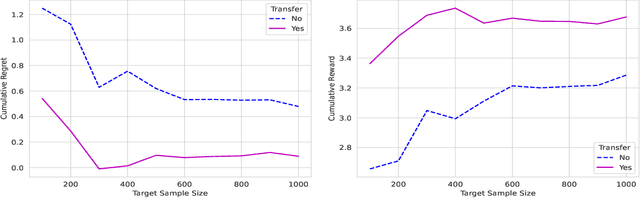
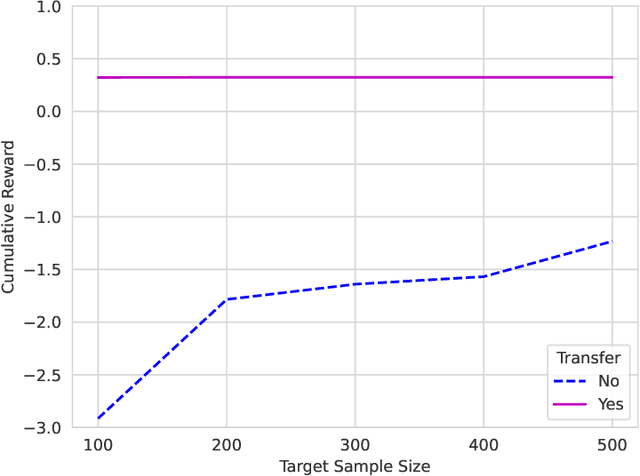
In dynamic decision-making scenarios across business and healthcare, leveraging sample trajectories from diverse populations can significantly enhance reinforcement learning (RL) performance for specific target populations, especially when sample sizes are limited. While existing transfer learning methods primarily focus on linear regression settings, they lack direct applicability to reinforcement learning algorithms. This paper pioneers the study of transfer learning for dynamic decision scenarios modeled by non-stationary finite-horizon Markov decision processes, utilizing neural networks as powerful function approximators and backward inductive learning. We demonstrate that naive sample pooling strategies, effective in regression settings, fail in Markov decision processes.To address this challenge, we introduce a novel ``re-weighted targeting procedure'' to construct ``transferable RL samples'' and propose ``transfer deep $Q^*$-learning'', enabling neural network approximation with theoretical guarantees. We assume that the reward functions are transferable and deal with both situations in which the transition densities are transferable or nontransferable. Our analytical techniques for transfer learning in neural network approximation and transition density transfers have broader implications, extending to supervised transfer learning with neural networks and domain shift scenarios. Empirical experiments on both synthetic and real datasets corroborate the advantages of our method, showcasing its potential for improving decision-making through strategically constructing transferable RL samples in non-stationary reinforcement learning contexts.

Learning Spectral Methods by Transformers

Transformers demonstrate significant advantages as the building block of modern LLMs. In this work, we study the capacities of Transformers in performing unsupervised learning. We show that multi-layered Transformers, given a sufficiently large set of pre-training instances, are able to learn the algorithms themselves and perform statistical estimation tasks given new instances. This learning paradigm is distinct from the in-context learning setup and is similar to the learning procedure of human brains where skills are learned through past experience. Theoretically, we prove that pre-trained Transformers can learn the spectral methods and use the classification of bi-class Gaussian mixture model as an example. Our proof is constructive using algorithmic design techniques. Our results are built upon the similarities of multi-layered Transformer architecture with the iterative recovery algorithms used in practice. Empirically, we verify the strong capacity of the multi-layered (pre-trained) Transformer on unsupervised learning through the lens of both the PCA and the Clustering tasks performed on the synthetic and real-world datasets.

Transformers Simulate MLE for Sequence Generation in Bayesian Networks

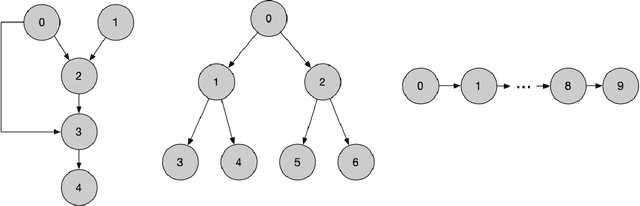
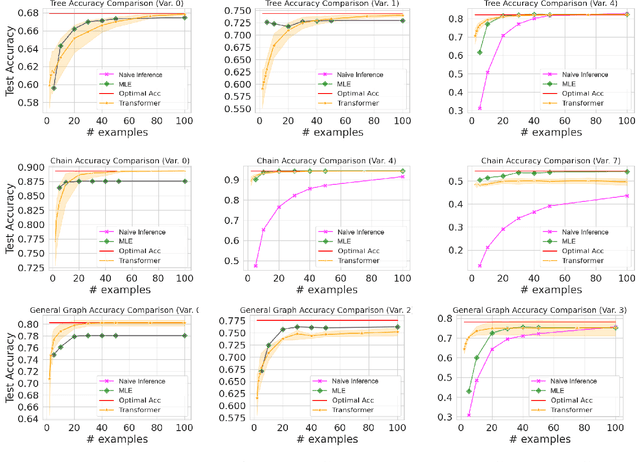
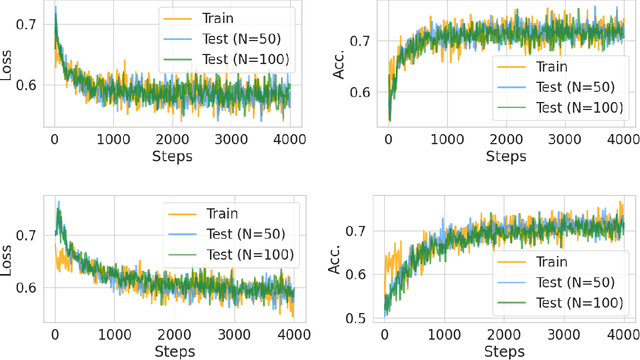
Transformers have achieved significant success in various fields, notably excelling in tasks involving sequential data like natural language processing. Despite these achievements, the theoretical understanding of transformers' capabilities remains limited. In this paper, we investigate the theoretical capabilities of transformers to autoregressively generate sequences in Bayesian networks based on in-context maximum likelihood estimation (MLE). Specifically, we consider a setting where a context is formed by a set of independent sequences generated according to a Bayesian network. We demonstrate that there exists a simple transformer model that can (i) estimate the conditional probabilities of the Bayesian network according to the context, and (ii) autoregressively generate a new sample according to the Bayesian network with estimated conditional probabilities. We further demonstrate in extensive experiments that such a transformer does not only exist in theory, but can also be effectively obtained through training. Our analysis highlights the potential of transformers to learn complex probabilistic models and contributes to a better understanding of large language models as a powerful class of sequence generators.

Localized exploration in contextual dynamic pricing achieves dimension-free regret

We study the problem of contextual dynamic pricing with a linear demand model. We propose a novel localized exploration-then-commit (LetC) algorithm which starts with a pure exploration stage, followed by a refinement stage that explores near the learned optimal pricing policy, and finally enters a pure exploitation stage. The algorithm is shown to achieve a minimax optimal, dimension-free regret bound when the time horizon exceeds a polynomial of the covariate dimension. Furthermore, we provide a general theoretical framework that encompasses the entire time spectrum, demonstrating how to balance exploration and exploitation when the horizon is limited. The analysis is powered by a novel critical inequality that depicts the exploration-exploitation trade-off in dynamic pricing, mirroring its existing counterpart for the bias-variance trade-off in regularized regression. Our theoretical results are validated by extensive experiments on synthetic and real-world data.

Benign Overfitting in Out-of-Distribution Generalization of Linear Models

Benign overfitting refers to the phenomenon where an over-parameterized model fits the training data perfectly, including noise in the data, but still generalizes well to the unseen test data. While prior work provides some theoretical understanding of this phenomenon under the in-distribution setup, modern machine learning often operates in a more challenging Out-of-Distribution (OOD) regime, where the target (test) distribution can be rather different from the source (training) distribution. In this work, we take an initial step towards understanding benign overfitting in the OOD regime by focusing on the basic setup of over-parameterized linear models under covariate shift. We provide non-asymptotic guarantees proving that benign overfitting occurs in standard ridge regression, even under the OOD regime when the target covariance satisfies certain structural conditions. We identify several vital quantities relating to source and target covariance, which govern the performance of OOD generalization. Our result is sharp, which provably recovers prior in-distribution benign overfitting guarantee [Tsigler and Bartlett, 2023], as well as under-parameterized OOD guarantee [Ge et al., 2024] when specializing to each setup. Moreover, we also present theoretical results for a more general family of target covariance matrix, where standard ridge regression only achieves a slow statistical rate of $O(1/\sqrt{n})$ for the excess risk, while Principal Component Regression (PCR) is guaranteed to achieve the fast rate $O(1/n)$, where $n$ is the number of samples.

One-Layer Transformer Provably Learns One-Nearest Neighbor In Context

Transformers have achieved great success in recent years. Interestingly, transformers have shown particularly strong in-context learning capability -- even without fine-tuning, they are still able to solve unseen tasks well purely based on task-specific prompts. In this paper, we study the capability of one-layer transformers in learning one of the most classical nonparametric estimators, the one-nearest neighbor prediction rule. Under a theoretical framework where the prompt contains a sequence of labeled training data and unlabeled test data, we show that, although the loss function is nonconvex when trained with gradient descent, a single softmax attention layer can successfully learn to behave like a one-nearest neighbor classifier. Our result gives a concrete example of how transformers can be trained to implement nonparametric machine learning algorithms, and sheds light on the role of softmax attention in transformer models.