Evo-MARL: Co-Evolutionary Multi-Agent Reinforcement Learning for Internalized Safety

Multi-agent systems (MAS) built on multimodal large language models exhibit strong collaboration and performance. However, their growing openness and interaction complexity pose serious risks, notably jailbreak and adversarial attacks. Existing defenses typically rely on external guard modules, such as dedicated safety agents, to handle unsafe behaviors. Unfortunately, this paradigm faces two challenges: (1) standalone agents offer limited protection, and (2) their independence leads to single-point failure-if compromised, system-wide safety collapses. Naively increasing the number of guard agents further raises cost and complexity. To address these challenges, we propose Evo-MARL, a novel multi-agent reinforcement learning (MARL) framework that enables all task agents to jointly acquire defensive capabilities. Rather than relying on external safety modules, Evo-MARL trains each agent to simultaneously perform its primary function and resist adversarial threats, ensuring robustness without increasing system overhead or single-node failure. Furthermore, Evo-MARL integrates evolutionary search with parameter-sharing reinforcement learning to co-evolve attackers and defenders. This adversarial training paradigm internalizes safety mechanisms and continually enhances MAS performance under co-evolving threats. Experiments show that Evo-MARL reduces attack success rates by up to 22% while boosting accuracy by up to 5% on reasoning tasks-demonstrating that safety and utility can be jointly improved.

Transformers and Their Roles as Time Series Foundation Models

We give a comprehensive analysis of transformers as time series foundation models, focusing on their approximation and generalization capabilities. First, we demonstrate that there exist transformers that fit an autoregressive model on input univariate time series via gradient descent. We then analyze MOIRAI, a multivariate time series foundation model capable of handling an arbitrary number of covariates. We prove that it is capable of automatically fitting autoregressive models with an arbitrary number of covariates, offering insights into its design and empirical success. For generalization, we establish bounds for pretraining when the data satisfies Dobrushin's condition. Experiments support our theoretical findings, highlighting the efficacy of transformers as time series foundation models.

Transformers Simulate MLE for Sequence Generation in Bayesian Networks

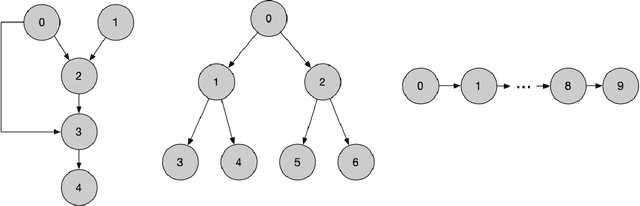
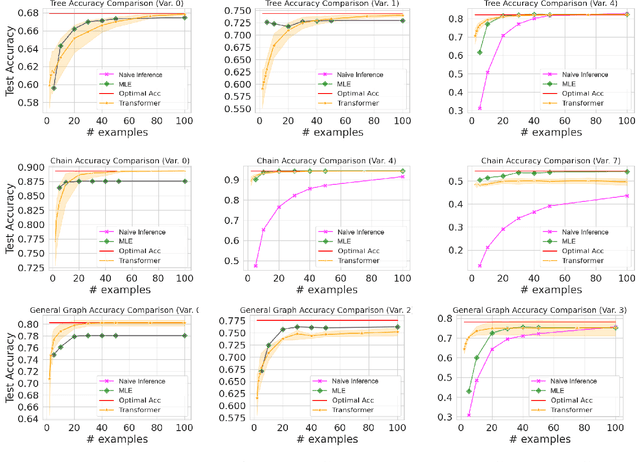
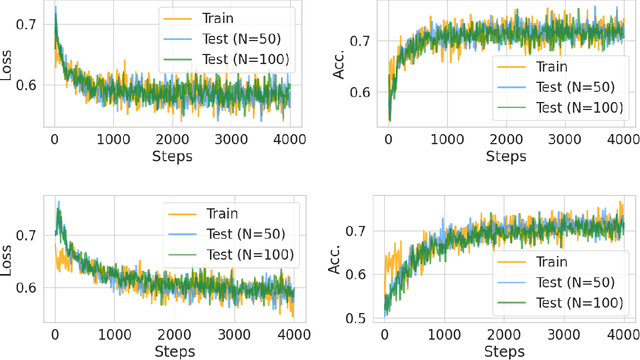
Transformers have achieved significant success in various fields, notably excelling in tasks involving sequential data like natural language processing. Despite these achievements, the theoretical understanding of transformers' capabilities remains limited. In this paper, we investigate the theoretical capabilities of transformers to autoregressively generate sequences in Bayesian networks based on in-context maximum likelihood estimation (MLE). Specifically, we consider a setting where a context is formed by a set of independent sequences generated according to a Bayesian network. We demonstrate that there exists a simple transformer model that can (i) estimate the conditional probabilities of the Bayesian network according to the context, and (ii) autoregressively generate a new sample according to the Bayesian network with estimated conditional probabilities. We further demonstrate in extensive experiments that such a transformer does not only exist in theory, but can also be effectively obtained through training. Our analysis highlights the potential of transformers to learn complex probabilistic models and contributes to a better understanding of large language models as a powerful class of sequence generators.

Learning Spectral Methods by Transformers

Transformers demonstrate significant advantages as the building block of modern LLMs. In this work, we study the capacities of Transformers in performing unsupervised learning. We show that multi-layered Transformers, given a sufficiently large set of pre-training instances, are able to learn the algorithms themselves and perform statistical estimation tasks given new instances. This learning paradigm is distinct from the in-context learning setup and is similar to the learning procedure of human brains where skills are learned through past experience. Theoretically, we prove that pre-trained Transformers can learn the spectral methods and use the classification of bi-class Gaussian mixture model as an example. Our proof is constructive using algorithmic design techniques. Our results are built upon the similarities of multi-layered Transformer architecture with the iterative recovery algorithms used in practice. Empirically, we verify the strong capacity of the multi-layered (pre-trained) Transformer on unsupervised learning through the lens of both the PCA and the Clustering tasks performed on the synthetic and real-world datasets.

Provably Optimal Memory Capacity for Modern Hopfield Models: Transformer-Compatible Dense Associative Memories as Spherical Codes

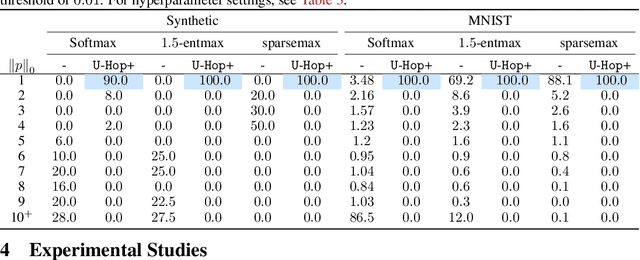
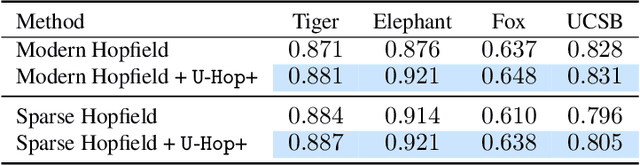
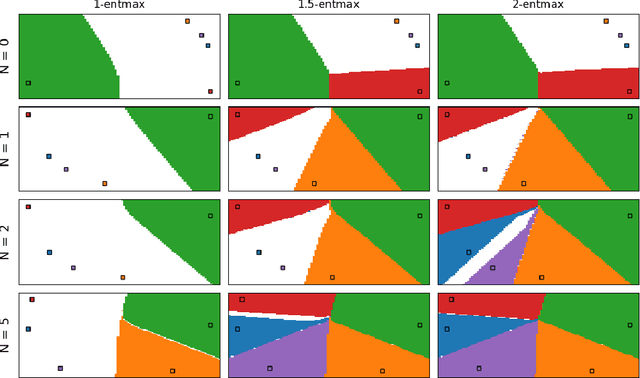
We study the optimal memorization capacity of modern Hopfield models and Kernelized Hopfield Models (KHMs), a transformer-compatible class of Dense Associative Memories. We present a tight analysis by establishing a connection between the memory configuration of KHMs and spherical codes from information theory. Specifically, we treat the stored memory set as a specialized spherical code. This enables us to cast the memorization problem in KHMs into a point arrangement problem on a hypersphere. We show that the optimal capacity of KHMs occurs when the feature space allows memories to form an optimal spherical code. This unique perspective leads to: (i) An analysis of how KHMs achieve optimal memory capacity, and identify corresponding necessary conditions. Importantly, we establish an upper capacity bound that matches the well-known exponential lower bound in the literature. This provides the first tight and optimal asymptotic memory capacity for modern Hopfield models. (ii) A sub-linear time algorithm $\mathtt{U}\text{-}\mathtt{Hop}$+ to reach KHMs' optimal capacity. (iii) An analysis of the scaling behavior of the required feature dimension relative to the number of stored memories. These efforts improve both the retrieval capability of KHMs and the representation learning of corresponding transformers. Experimentally, we provide thorough numerical results to back up theoretical findings.

Nonparametric Modern Hopfield Models

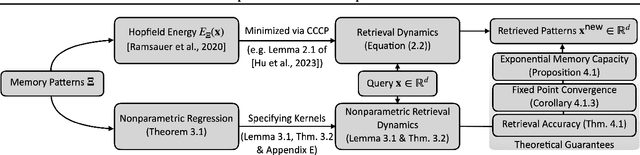
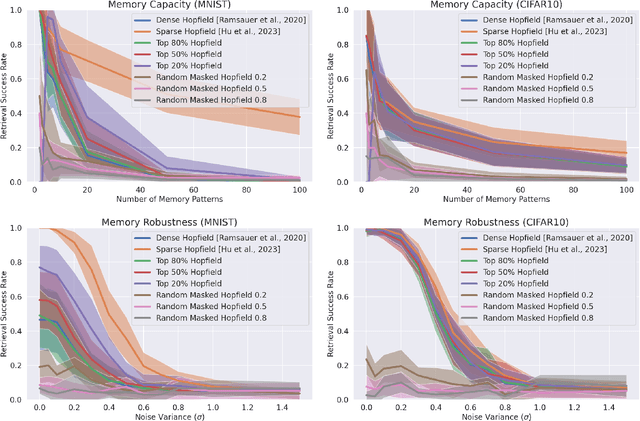
We present a nonparametric construction for deep learning compatible modern Hopfield models and utilize this framework to debut an efficient variant. Our key contribution stems from interpreting the memory storage and retrieval processes in modern Hopfield models as a nonparametric regression problem subject to a set of query-memory pairs. Crucially, our framework not only recovers the known results from the original dense modern Hopfield model but also fills the void in the literature regarding efficient modern Hopfield models, by introducing \textit{sparse-structured} modern Hopfield models with sub-quadratic complexity. We establish that this sparse model inherits the appealing theoretical properties of its dense analogue -- connection with transformer attention, fixed point convergence and exponential memory capacity -- even without knowing details of the Hopfield energy function. Additionally, we showcase the versatility of our framework by constructing a family of modern Hopfield models as extensions, including linear, random masked, top-$K$ and positive random feature modern Hopfield models. Empirically, we validate the efficacy of our framework in both synthetic and realistic settings.

Uniform Memory Retrieval with Larger Capacity for Modern Hopfield Models

We propose a two-stage memory retrieval dynamics for modern Hopfield models, termed $\mathtt{U\text{-}Hop}$, with enhanced memory capacity. Our key contribution is a learnable feature map $\Phi$ which transforms the Hopfield energy function into a kernel space. This transformation ensures convergence between the local minima of energy and the fixed points of retrieval dynamics within the kernel space. Consequently, the kernel norm induced by $\Phi$ serves as a novel similarity measure. It utilizes the stored memory patterns as learning data to enhance memory capacity across all modern Hopfield models. Specifically, we accomplish this by constructing a separation loss $\mathcal{L}_\Phi$ that separates the local minima of kernelized energy by separating stored memory patterns in kernel space. Methodologically, $\mathtt{U\text{-}Hop}$ memory retrieval process consists of: \textbf{(Stage~I.)} minimizing separation loss for a more uniformed memory (local minimum) distribution, followed by \textbf{(Stage~II.)} standard Hopfield energy minimization for memory retrieval. This results in a significant reduction of possible meta-stable states in the Hopfield energy function, thus enhancing memory capacity by preventing memory confusion. Empirically, with real-world datasets, we demonstrate that $\mathtt{U\text{-}Hop}$ outperforms all existing modern Hopfield models and SOTA similarity measures, achieving substantial improvements in both associative memory retrieval and deep learning tasks.

STanHop: Sparse Tandem Hopfield Model for Memory-Enhanced Time Series Prediction

We present STanHop-Net (Sparse Tandem Hopfield Network) for multivariate time series prediction with memory-enhanced capabilities. At the heart of our approach is STanHop, a novel Hopfield-based neural network block, which sparsely learns and stores both temporal and cross-series representations in a data-dependent fashion. In essence, STanHop sequentially learn temporal representation and cross-series representation using two tandem sparse Hopfield layers. In addition, StanHop incorporates two additional external memory modules: a Plug-and-Play module and a Tune-and-Play module for train-less and task-aware memory-enhancements, respectively. They allow StanHop-Net to swiftly respond to certain sudden events. Methodologically, we construct the StanHop-Net by stacking STanHop blocks in a hierarchical fashion, enabling multi-resolution feature extraction with resolution-specific sparsity. Theoretically, we introduce a sparse extension of the modern Hopfield model (Generalized Sparse Modern Hopfield Model) and show that it endows a tighter memory retrieval error compared to the dense counterpart without sacrificing memory capacity. Empirically, we validate the efficacy of our framework on both synthetic and real-world settings.

On Sparse Modern Hopfield Model

We introduce the sparse modern Hopfield model as a sparse extension of the modern Hopfield model. Like its dense counterpart, the sparse modern Hopfield model equips a memory-retrieval dynamics whose one-step approximation corresponds to the sparse attention mechanism. Theoretically, our key contribution is a principled derivation of a closed-form sparse Hopfield energy using the convex conjugate of the sparse entropic regularizer. Building upon this, we derive the sparse memory retrieval dynamics from the sparse energy function and show its one-step approximation is equivalent to the sparse-structured attention. Importantly, we provide a sparsity-dependent memory retrieval error bound which is provably tighter than its dense analog. The conditions for the benefits of sparsity to arise are therefore identified and discussed. In addition, we show that the sparse modern Hopfield model maintains the robust theoretical properties of its dense counterpart, including rapid fixed point convergence and exponential memory capacity. Empirically, we use both synthetic and real-world datasets to demonstrate that the sparse Hopfield model outperforms its dense counterpart in many situations.

HonestBait: Forward References for Attractive but Faithful Headline Generation

Current methods for generating attractive headlines often learn directly from data, which bases attractiveness on the number of user clicks and views. Although clicks or views do reflect user interest, they can fail to reveal how much interest is raised by the writing style and how much is due to the event or topic itself. Also, such approaches can lead to harmful inventions by over-exaggerating the content, aggravating the spread of false information. In this work, we propose HonestBait, a novel framework for solving these issues from another aspect: generating headlines using forward references (FRs), a writing technique often used for clickbait. A self-verification process is included during training to avoid spurious inventions. We begin with a preliminary user study to understand how FRs affect user interest, after which we present PANCO1, an innovative dataset containing pairs of fake news with verified news for attractive but faithful news headline generation. Automatic metrics and human evaluations show that our framework yields more attractive results (+11.25% compared to human-written verified news headlines) while maintaining high veracity, which helps promote real information to fight against fake news.