Nonparametric Modern Hopfield Models
Paper and Code
Apr 05, 2024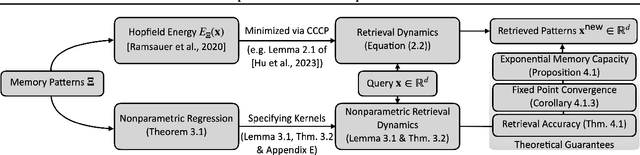
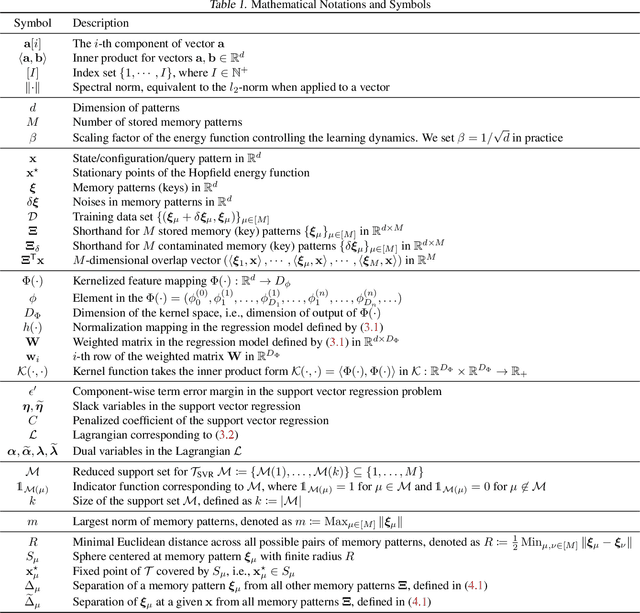
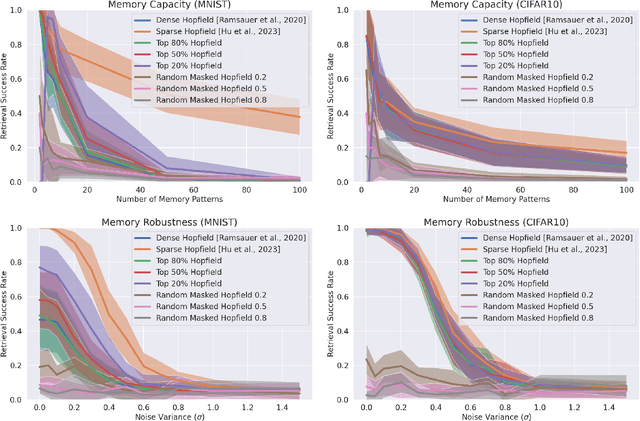
We present a nonparametric construction for deep learning compatible modern Hopfield models and utilize this framework to debut an efficient variant. Our key contribution stems from interpreting the memory storage and retrieval processes in modern Hopfield models as a nonparametric regression problem subject to a set of query-memory pairs. Crucially, our framework not only recovers the known results from the original dense modern Hopfield model but also fills the void in the literature regarding efficient modern Hopfield models, by introducing \textit{sparse-structured} modern Hopfield models with sub-quadratic complexity. We establish that this sparse model inherits the appealing theoretical properties of its dense analogue -- connection with transformer attention, fixed point convergence and exponential memory capacity -- even without knowing details of the Hopfield energy function. Additionally, we showcase the versatility of our framework by constructing a family of modern Hopfield models as extensions, including linear, random masked, top-$K$ and positive random feature modern Hopfield models. Empirically, we validate the efficacy of our framework in both synthetic and realistic settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge