On Flow Matching KL Divergence

We derive a deterministic, non-asymptotic upper bound on the Kullback-Leibler (KL) divergence of the flow-matching distribution approximation. In particular, if the $L_2$ flow-matching loss is bounded by $\epsilon^2 > 0$, then the KL divergence between the true data distribution and the estimated distribution is bounded by $A_1 \epsilon + A_2 \epsilon^2$. Here, the constants $A_1$ and $A_2$ depend only on the regularities of the data and velocity fields. Consequently, this bound implies statistical convergence rates of Flow Matching Transformers under the Total Variation (TV) distance. We show that, flow matching achieves nearly minimax-optimal efficiency in estimating smooth distributions. Our results make the statistical efficiency of flow matching comparable to that of diffusion models under the TV distance. Numerical studies on synthetic and learned velocities corroborate our theory.

On Structured State-Space Duality

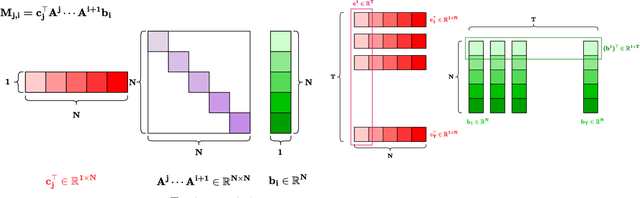
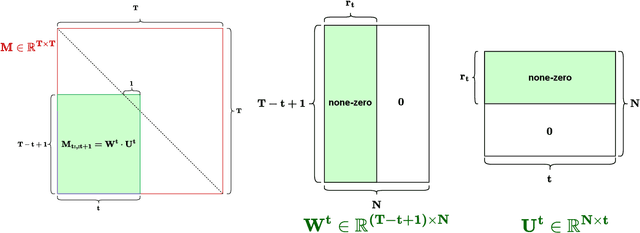
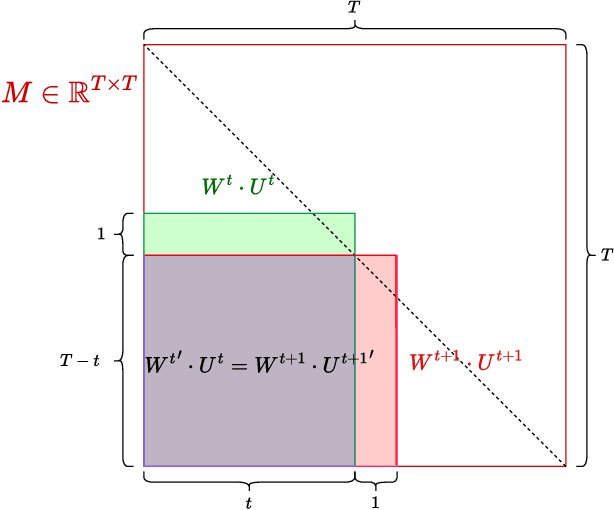
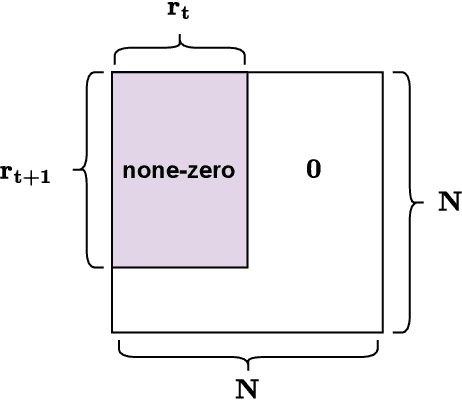
Structured State-Space Duality (SSD) [Dao & Gu, ICML 2024] is an equivalence between a simple Structured State-Space Model (SSM) and a masked attention mechanism. In particular, a state-space model with a scalar-times-identity state matrix is equivalent to a masked self-attention with a $1$-semiseparable causal mask. Consequently, the same sequence transformation (model) has two algorithmic realizations: as a linear-time $O(T)$ recurrence or as a quadratic-time $O(T^2)$ attention. In this note, we formalize and generalize this duality: (i) we extend SSD from the scalar-identity case to general diagonal SSMs (diagonal state matrices); (ii) we show that these diagonal SSMs match the scalar case's training complexity lower bounds while supporting richer dynamics; (iii) we establish a necessary and sufficient condition under which an SSM is equivalent to $1$-semiseparable masked attention; and (iv) we show that such duality fails to extend to standard softmax attention due to rank explosion. Together, these results tighten bridge between recurrent SSMs and Transformers, and widen the design space for expressive yet efficient sequence models.

A Theoretical Analysis of Discrete Flow Matching Generative Models

We provide a theoretical analysis for end-to-end training Discrete Flow Matching (DFM) generative models. DFM is a promising discrete generative modeling framework that learns the underlying generative dynamics by training a neural network to approximate the transformative velocity field. Our analysis establishes a clear chain of guarantees by decomposing the final distribution estimation error. We first prove that the total variation distance between the generated and target distributions is controlled by the risk of the learned velocity field. We then bound this risk by analyzing its two primary sources: (i) Approximation Error, where we quantify the capacity of the Transformer architecture to represent the true velocity, and (ii) Estimation Error, where we derive statistical convergence rates that bound the error from training on a finite dataset. By composing these results, we provide the first formal proof that the distribution generated by a trained DFM model provably converges to the true data distribution as the training set size increases.

In-Context Algorithm Emulation in Fixed-Weight Transformers

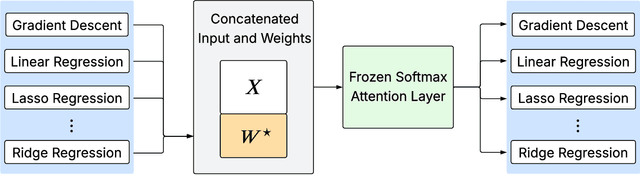
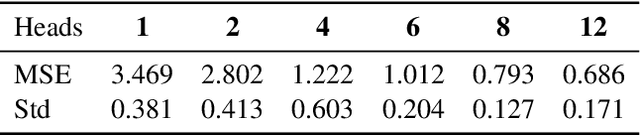
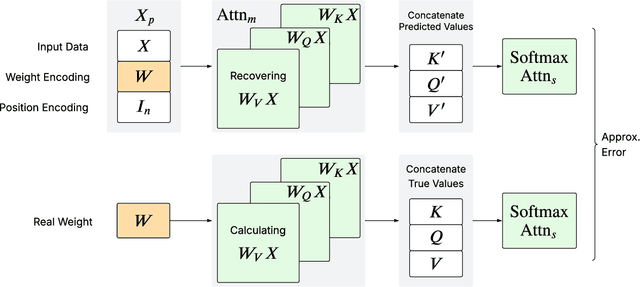
We prove that a minimal Transformer architecture with frozen weights is capable of emulating a broad class of algorithms by in-context prompting. In particular, for any algorithm implementable by a fixed-weight attention head (e.g. one-step gradient descent or linear/ridge regression), there exists a prompt that drives a two-layer softmax attention module to reproduce the algorithm's output with arbitrary precision. This guarantee extends even to a single-head attention layer (using longer prompts if necessary), achieving architectural minimality. Our key idea is to construct prompts that encode an algorithm's parameters into token representations, creating sharp dot-product gaps that force the softmax attention to follow the intended computation. This construction requires no feed-forward layers and no parameter updates. All adaptation happens through the prompt alone. These findings forge a direct link between in-context learning and algorithmic emulation, and offer a simple mechanism for large Transformers to serve as prompt-programmable libraries of algorithms. They illuminate how GPT-style foundation models may swap algorithms via prompts alone, establishing a form of algorithmic universality in modern Transformer models.

Minimalist Softmax Attention Provably Learns Constrained Boolean Functions

We study the computational limits of learning $k$-bit Boolean functions (specifically, $\mathrm{AND}$, $\mathrm{OR}$, and their noisy variants), using a minimalist single-head softmax-attention mechanism, where $k=\Theta(d)$ relevant bits are selected from $d$ inputs. We show that these simple $\mathrm{AND}$ and $\mathrm{OR}$ functions are unsolvable with a single-head softmax-attention mechanism alone. However, with teacher forcing, the same minimalist attention is capable of solving them. These findings offer two key insights: Architecturally, solving these Boolean tasks requires only minimalist attention, without deep Transformer blocks or FFNs. Methodologically, one gradient descent update with supervision suffices and replaces the multi-step Chain-of-Thought (CoT) reasoning scheme of [Kim and Suzuki, ICLR 2025] for solving Boolean problems. Together, the bounds expose a fundamental gap between what this minimal architecture achieves under ideal supervision and what is provably impossible under standard training.

Latent Variable Estimation in Bayesian Black-Litterman Models

We revisit the Bayesian Black-Litterman (BL) portfolio model and remove its reliance on subjective investor views. Classical BL requires an investor "view": a forecast vector $q$ and its uncertainty matrix $\Omega$ that describe how much a chosen portfolio should outperform the market. Our key idea is to treat $(q,\Omega)$ as latent variables and learn them from market data within a single Bayesian network. Consequently, the resulting posterior estimation admits closed-form expression, enabling fast inference and stable portfolio weights. Building on these, we propose two mechanisms to capture how features interact with returns: shared-latent parametrization and feature-influenced views; both recover classical BL and Markowitz portfolios as special cases. Empirically, on 30-year Dow-Jones and 20-year sector-ETF data, we improve Sharpe ratios by 50% and cut turnover by 55% relative to Markowitz and the index baselines. This work turns BL into a fully data-driven, view-free, and coherent Bayesian framework for portfolio optimization.

Fast and Low-Cost Genomic Foundation Models via Outlier Removal

We propose the first unified adversarial attack benchmark for Genomic Foundation Models (GFMs), named GERM. Unlike existing GFM benchmarks, GERM offers the first comprehensive evaluation framework to systematically assess the vulnerability of GFMs to adversarial attacks. Methodologically, we evaluate the adversarial robustness of five state-of-the-art GFMs using four widely adopted attack algorithms and three defense strategies. Importantly, our benchmark provides an accessible and comprehensive framework to analyze GFM vulnerabilities with respect to model architecture, quantization schemes, and training datasets. Empirically, transformer-based models exhibit greater robustness to adversarial perturbations compared to HyenaDNA, highlighting the impact of architectural design on vulnerability. Moreover, adversarial attacks frequently target biologically significant genomic regions, suggesting that these models effectively capture meaningful sequence features.

Attention Mechanism, Max-Affine Partition, and Universal Approximation

We establish the universal approximation capability of single-layer, single-head self- and cross-attention mechanisms with minimal attached structures. Our key insight is to interpret single-head attention as an input domain-partition mechanism that assigns distinct values to subregions. This allows us to engineer the attention weights such that this assignment imitates the target function. Building on this, we prove that a single self-attention layer, preceded by sum-of-linear transformations, is capable of approximating any continuous function on a compact domain under the $L_\infty$-norm. Furthermore, we extend this construction to approximate any Lebesgue integrable function under $L_p$-norm for $1\leq p <\infty$. Lastly, we also extend our techniques and show that, for the first time, single-head cross-attention achieves the same universal approximation guarantees.

Universal Approximation with Softmax Attention

We prove that with linear transformations, both (i) two-layer self-attention and (ii) one-layer self-attention followed by a softmax function are universal approximators for continuous sequence-to-sequence functions on compact domains. Our main technique is a new interpolation-based method for analyzing attention's internal mechanism. This leads to our key insight: self-attention is able to approximate a generalized version of ReLU to arbitrary precision, and hence subsumes many known universal approximators. Building on these, we show that two-layer multi-head attention alone suffices as a sequence-to-sequence universal approximator. In contrast, prior works rely on feed-forward networks to establish universal approximation in Transformers. Furthermore, we extend our techniques to show that, (softmax-)attention-only layers are capable of approximating various statistical models in-context. We believe these techniques hold independent interest.

NdLinear Is All You Need for Representation Learning

Many high-impact machine learning tasks involve multi-dimensional data (e.g., images, volumetric medical scans, multivariate time-series). Yet, most neural architectures flatten inputs, discarding critical cross-dimension information. We introduce NdLinear, a novel linear transformation that preserves these structures without extra overhead. By operating separately along each dimension, NdLinear captures dependencies that standard fully connected layers overlook. Extensive experiments across convolutional, recurrent, and transformer-based networks show significant improvements in representational power and parameter efficiency. Crucially, NdLinear serves as a foundational building block for large-scale foundation models by operating on any unimodal or multimodal data in its native form. This removes the need for flattening or modality-specific preprocessing. Ndlinear rethinks core architectural priorities beyond attention, enabling more expressive, context-aware models at scale. We propose NdLinear as a drop-in replacement for standard linear layers -- marking an important step toward next-generation neural architectures.