Differentially Private Kernel Density Estimation

We introduce a refined differentially private (DP) data structure for kernel density estimation (KDE), offering not only improved privacy-utility tradeoff but also better efficiency over prior results. Specifically, we study the mathematical problem: given a similarity function $f$ (or DP KDE) and a private dataset $X \subset \mathbb{R}^d$, our goal is to preprocess $X$ so that for any query $y\in\mathbb{R}^d$, we approximate $\sum_{x \in X} f(x, y)$ in a differentially private fashion. The best previous algorithm for $f(x,y) =\| x - y \|_1$ is the node-contaminated balanced binary tree by [Backurs, Lin, Mahabadi, Silwal, and Tarnawski, ICLR 2024]. Their algorithm requires $O(nd)$ space and time for preprocessing with $n=|X|$. For any query point, the query time is $d \log n$, with an error guarantee of $(1+\alpha)$-approximation and $\epsilon^{-1} \alpha^{-0.5} d^{1.5} R \log^{1.5} n$. In this paper, we improve the best previous result [Backurs, Lin, Mahabadi, Silwal, and Tarnawski, ICLR 2024] in three aspects: - We reduce query time by a factor of $\alpha^{-1} \log n$. - We improve the approximation ratio from $\alpha$ to 1. - We reduce the error dependence by a factor of $\alpha^{-0.5}$. From a technical perspective, our method of constructing the search tree differs from previous work [Backurs, Lin, Mahabadi, Silwal, and Tarnawski, ICLR 2024]. In prior work, for each query, the answer is split into $\alpha^{-1} \log n$ numbers, each derived from the summation of $\log n$ values in interval tree countings. In contrast, we construct the tree differently, splitting the answer into $\log n$ numbers, where each is a smart combination of two distance values, two counting values, and $y$ itself. We believe our tree structure may be of independent interest.

Feature Programming for Multivariate Time Series Prediction

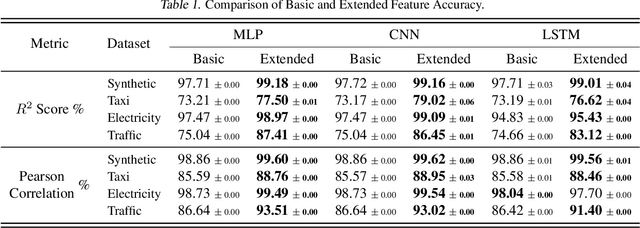
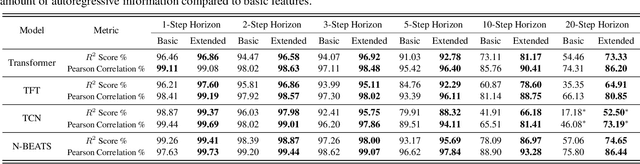
We introduce the concept of programmable feature engineering for time series modeling and propose a feature programming framework. This framework generates large amounts of predictive features for noisy multivariate time series while allowing users to incorporate their inductive bias with minimal effort. The key motivation of our framework is to view any multivariate time series as a cumulative sum of fine-grained trajectory increments, with each increment governed by a novel spin-gas dynamical Ising model. This fine-grained perspective motivates the development of a parsimonious set of operators that summarize multivariate time series in an abstract fashion, serving as the foundation for large-scale automated feature engineering. Numerically, we validate the efficacy of our method on several synthetic and real-world noisy time series datasets.

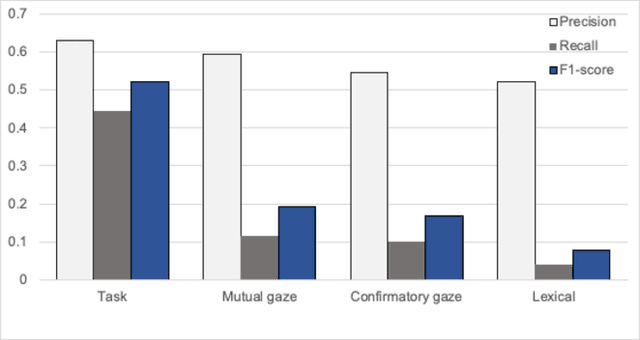
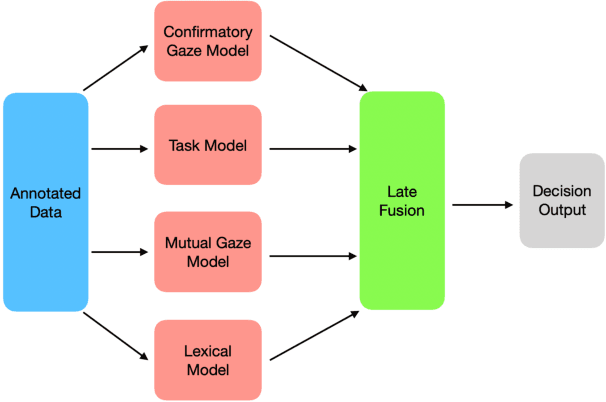
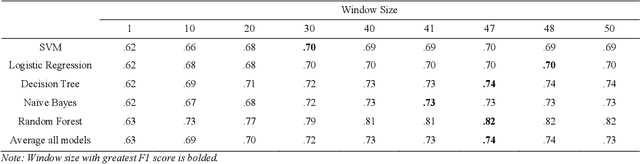
Supporting User Autonomy with Multimodal Fusion to Detect when a User Needs Assistance from a Social Robot

It is crucial for any assistive robot to prioritize the autonomy of the user. For a robot working in a task setting to effectively maintain a user's autonomy it must provide timely assistance and make accurate decisions. We use four independent high-precision, low-recall models, a mutual gaze model, task model, confirmatory gaze model, and a lexical model, that predict a user's need for assistance. Improving upon our four independent models, we used a sliding window method and a random forest classification algorithm to capture temporal dependencies and fuse the independent models with a late fusion approach. The late fusion approach strongly outperforms all four of the independent models providing a more wholesome approach with greater accuracy to better assist the user while maintaining their autonomy. These results can provide insight into the potential of including additional modalities and utilizing assistive robots in more task settings.