Diffusion Transformers for Imputation: Statistical Efficiency and Uncertainty Quantification

Imputation methods play a critical role in enhancing the quality of practical time-series data, which often suffer from pervasive missing values. Recently, diffusion-based generative imputation methods have demonstrated remarkable success compared to autoregressive and conventional statistical approaches. Despite their empirical success, the theoretical understanding of how well diffusion-based models capture complex spatial and temporal dependencies between the missing values and observed ones remains limited. Our work addresses this gap by investigating the statistical efficiency of conditional diffusion transformers for imputation and quantifying the uncertainty in missing values. Specifically, we derive statistical sample complexity bounds based on a novel approximation theory for conditional score functions using transformers, and, through this, construct tight confidence regions for missing values. Our findings also reveal that the efficiency and accuracy of imputation are significantly influenced by the missing patterns. Furthermore, we validate these theoretical insights through simulation and propose a mixed-masking training strategy to enhance the imputation performance.

Diffusion Factor Models: Generating High-Dimensional Returns with Factor Structure

Financial scenario simulation is essential for risk management and portfolio optimization, yet it remains challenging especially in high-dimensional and small data settings common in finance. We propose a diffusion factor model that integrates latent factor structure into generative diffusion processes, bridging econometrics with modern generative AI to address the challenges of the curse of dimensionality and data scarcity in financial simulation. By exploiting the low-dimensional factor structure inherent in asset returns, we decompose the score function--a key component in diffusion models--using time-varying orthogonal projections, and this decomposition is incorporated into the design of neural network architectures. We derive rigorous statistical guarantees, establishing nonasymptotic error bounds for both score estimation at O(d^{5/2} n^{-2/(k+5)}) and generated distribution at O(d^{5/4} n^{-1/2(k+5)}), primarily driven by the intrinsic factor dimension k rather than the number of assets d, surpassing the dimension-dependent limits in the classical nonparametric statistics literature and making the framework viable for markets with thousands of assets. Numerical studies confirm superior performance in latent subspace recovery under small data regimes. Empirical analysis demonstrates the economic significance of our framework in constructing mean-variance optimal portfolios and factor portfolios. This work presents the first theoretical integration of factor structure with diffusion models, offering a principled approach for high-dimensional financial simulation with limited data.

On Statistical Rates of Conditional Diffusion Transformers: Approximation, Estimation and Minimax Optimality

We investigate the approximation and estimation rates of conditional diffusion transformers (DiTs) with classifier-free guidance. We present a comprehensive analysis for ``in-context'' conditional DiTs under four common data assumptions. We show that both conditional DiTs and their latent variants lead to the minimax optimality of unconditional DiTs under identified settings. Specifically, we discretize the input domains into infinitesimal grids and then perform a term-by-term Taylor expansion on the conditional diffusion score function under H\"older smooth data assumption. This enables fine-grained use of transformers' universal approximation through a more detailed piecewise constant approximation and hence obtains tighter bounds. Additionally, we extend our analysis to the latent setting under the linear latent subspace assumption. We not only show that latent conditional DiTs achieve lower bounds than conditional DiTs both in approximation and estimation, but also show the minimax optimality of latent unconditional DiTs. Our findings establish statistical limits for conditional and unconditional DiTs, and offer practical guidance toward developing more efficient and accurate DiT models.

A Theoretical Perspective for Speculative Decoding Algorithm

Transformer-based autoregressive sampling has been the major bottleneck for slowing down large language model inferences. One effective way to accelerate inference is \emph{Speculative Decoding}, which employs a small model to sample a sequence of draft tokens and a large model to validate. Given its empirical effectiveness, the theoretical understanding of Speculative Decoding is falling behind. This paper tackles this gap by conceptualizing the decoding problem via markov chain abstraction and studying the key properties, \emph{output quality and inference acceleration}, from a theoretical perspective. Our analysis covers the theoretical limits of speculative decoding, batch algorithms, and output quality-inference acceleration tradeoffs. Our results reveal the fundamental connections between different components of LLMs via total variation distances and show how they jointly affect the efficiency of decoding algorithms.

Diffusion Transformer Captures Spatial-Temporal Dependencies: A Theory for Gaussian Process Data

Diffusion Transformer, the backbone of Sora for video generation, successfully scales the capacity of diffusion models, pioneering new avenues for high-fidelity sequential data generation. Unlike static data such as images, sequential data consists of consecutive data frames indexed by time, exhibiting rich spatial and temporal dependencies. These dependencies represent the underlying dynamic model and are critical to validate the generated data. In this paper, we make the first theoretical step towards bridging diffusion transformers for capturing spatial-temporal dependencies. Specifically, we establish score approximation and distribution estimation guarantees of diffusion transformers for learning Gaussian process data with covariance functions of various decay patterns. We highlight how the spatial-temporal dependencies are captured and affect learning efficiency. Our study proposes a novel transformer approximation theory, where the transformer acts to unroll an algorithm. We support our theoretical results by numerical experiments, providing strong evidence that spatial-temporal dependencies are captured within attention layers, aligning with our approximation theory.

Provable Statistical Rates for Consistency Diffusion Models

Diffusion models have revolutionized various application domains, including computer vision and audio generation. Despite the state-of-the-art performance, diffusion models are known for their slow sample generation due to the extensive number of steps involved. In response, consistency models have been developed to merge multiple steps in the sampling process, thereby significantly boosting the speed of sample generation without compromising quality. This paper contributes towards the first statistical theory for consistency models, formulating their training as a distribution discrepancy minimization problem. Our analysis yields statistical estimation rates based on the Wasserstein distance for consistency models, matching those of vanilla diffusion models. Additionally, our results encompass the training of consistency models through both distillation and isolation methods, demystifying their underlying advantage.

Gradient Guidance for Diffusion Models: An Optimization Perspective

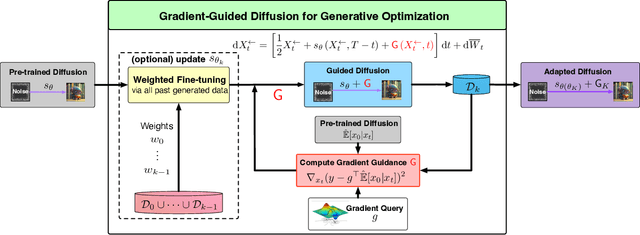
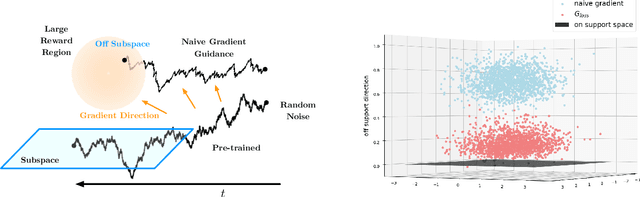
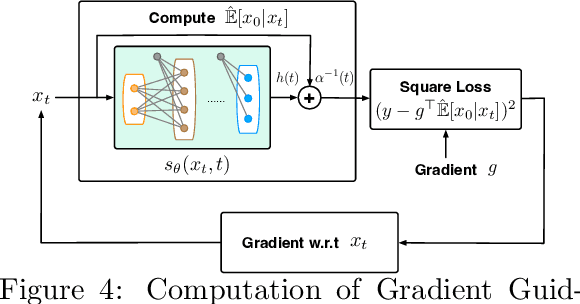
Diffusion models have demonstrated empirical successes in various applications and can be adapted to task-specific needs via guidance. This paper introduces a form of gradient guidance for adapting or fine-tuning diffusion models towards user-specified optimization objectives. We study the theoretic aspects of a guided score-based sampling process, linking the gradient-guided diffusion model to first-order optimization. We show that adding gradient guidance to the sampling process of a pre-trained diffusion model is essentially equivalent to solving a regularized optimization problem, where the regularization term acts as a prior determined by the pre-training data. Diffusion models are able to learn data's latent subspace, however, explicitly adding the gradient of an external objective function to the sample process would jeopardize the structure in generated samples. To remedy this issue, we consider a modified form of gradient guidance based on a forward prediction loss, which leverages the pre-trained score function to preserve the latent structure in generated samples. We further consider an iteratively fine-tuned version of gradient-guided diffusion where one can query gradients at newly generated data points and update the score network using new samples. This process mimics a first-order optimization iteration in expectation, for which we proved O(1/K) convergence rate to the global optimum when the objective function is concave.

An Overview of Diffusion Models: Applications, Guided Generation, Statistical Rates and Optimization

Diffusion models, a powerful and universal generative AI technology, have achieved tremendous success in computer vision, audio, reinforcement learning, and computational biology. In these applications, diffusion models provide flexible high-dimensional data modeling, and act as a sampler for generating new samples under active guidance towards task-desired properties. Despite the significant empirical success, theory of diffusion models is very limited, potentially slowing down principled methodological innovations for further harnessing and improving diffusion models. In this paper, we review emerging applications of diffusion models, understanding their sample generation under various controls. Next, we overview the existing theories of diffusion models, covering their statistical properties and sampling capabilities. We adopt a progressive routine, beginning with unconditional diffusion models and connecting to conditional counterparts. Further, we review a new avenue in high-dimensional structured optimization through conditional diffusion models, where searching for solutions is reformulated as a conditional sampling problem and solved by diffusion models. Lastly, we discuss future directions about diffusion models. The purpose of this paper is to provide a well-rounded theoretical exposure for stimulating forward-looking theories and methods of diffusion models.

Diffusion Model for Data-Driven Black-Box Optimization

Generative AI has redefined artificial intelligence, enabling the creation of innovative content and customized solutions that drive business practices into a new era of efficiency and creativity. In this paper, we focus on diffusion models, a powerful generative AI technology, and investigate their potential for black-box optimization over complex structured variables. Consider the practical scenario where one wants to optimize some structured design in a high-dimensional space, based on massive unlabeled data (representing design variables) and a small labeled dataset. We study two practical types of labels: 1) noisy measurements of a real-valued reward function and 2) human preference based on pairwise comparisons. The goal is to generate new designs that are near-optimal and preserve the designed latent structures. Our proposed method reformulates the design optimization problem into a conditional sampling problem, which allows us to leverage the power of diffusion models for modeling complex distributions. In particular, we propose a reward-directed conditional diffusion model, to be trained on the mixed data, for sampling a near-optimal solution conditioned on high predicted rewards. Theoretically, we establish sub-optimality error bounds for the generated designs. The sub-optimality gap nearly matches the optimal guarantee in off-policy bandits, demonstrating the efficiency of reward-directed diffusion models for black-box optimization. Moreover, when the data admits a low-dimensional latent subspace structure, our model efficiently generates high-fidelity designs that closely respect the latent structure. We provide empirical experiments validating our model in decision-making and content-creation tasks.

Unveil Conditional Diffusion Models with Classifier-free Guidance: A Sharp Statistical Theory

Conditional diffusion models serve as the foundation of modern image synthesis and find extensive application in fields like computational biology and reinforcement learning. In these applications, conditional diffusion models incorporate various conditional information, such as prompt input, to guide the sample generation towards desired properties. Despite the empirical success, theory of conditional diffusion models is largely missing. This paper bridges this gap by presenting a sharp statistical theory of distribution estimation using conditional diffusion models. Our analysis yields a sample complexity bound that adapts to the smoothness of the data distribution and matches the minimax lower bound. The key to our theoretical development lies in an approximation result for the conditional score function, which relies on a novel diffused Taylor approximation technique. Moreover, we demonstrate the utility of our statistical theory in elucidating the performance of conditional diffusion models across diverse applications, including model-based transition kernel estimation in reinforcement learning, solving inverse problems, and reward conditioned sample generation.