Renyuan Xu
Conditional Diffusion Guidance under Hard Constraint: A Stochastic Analysis Approach
Feb 05, 2026Abstract:We study conditional generation in diffusion models under hard constraints, where generated samples must satisfy prescribed events with probability one. Such constraints arise naturally in safety-critical applications and in rare-event simulation, where soft or reward-based guidance methods offer no guarantee of constraint satisfaction. Building on a probabilistic interpretation of diffusion models, we develop a principled conditional diffusion guidance framework based on Doob's h-transform, martingale representation and quadratic variation process. Specifically, the resulting guided dynamics augment a pretrained diffusion with an explicit drift correction involving the logarithmic gradient of a conditioning function, without modifying the pretrained score network. Leveraging martingale and quadratic-variation identities, we propose two novel off-policy learning algorithms based on a martingale loss and a martingale-covariation loss to estimate h and its gradient using only trajectories from the pretrained model. We provide non-asymptotic guarantees for the resulting conditional sampler in both total variation and Wasserstein distances, explicitly characterizing the impact of score approximation and guidance estimation errors. Numerical experiments demonstrate the effectiveness of the proposed methods in enforcing hard constraints and generating rare-event samples.
Adaptive Partitioning and Learning for Stochastic Control of Diffusion Processes
Dec 17, 2025Abstract:We study reinforcement learning for controlled diffusion processes with unbounded continuous state spaces, bounded continuous actions, and polynomially growing rewards: settings that arise naturally in finance, economics, and operations research. To overcome the challenges of continuous and high-dimensional domains, we introduce a model-based algorithm that adaptively partitions the joint state-action space. The algorithm maintains estimators of drift, volatility, and rewards within each partition, refining the discretization whenever estimation bias exceeds statistical confidence. This adaptive scheme balances exploration and approximation, enabling efficient learning in unbounded domains. Our analysis establishes regret bounds that depend on the problem horizon, state dimension, reward growth order, and a newly defined notion of zooming dimension tailored to unbounded diffusion processes. The bounds recover existing results for bounded settings as a special case, while extending theoretical guarantees to a broader class of diffusion-type problems. Finally, we validate the effectiveness of our approach through numerical experiments, including applications to high-dimensional problems such as multi-asset mean-variance portfolio selection.
Diffusion Factor Models: Generating High-Dimensional Returns with Factor Structure
Apr 09, 2025Abstract:Financial scenario simulation is essential for risk management and portfolio optimization, yet it remains challenging especially in high-dimensional and small data settings common in finance. We propose a diffusion factor model that integrates latent factor structure into generative diffusion processes, bridging econometrics with modern generative AI to address the challenges of the curse of dimensionality and data scarcity in financial simulation. By exploiting the low-dimensional factor structure inherent in asset returns, we decompose the score function--a key component in diffusion models--using time-varying orthogonal projections, and this decomposition is incorporated into the design of neural network architectures. We derive rigorous statistical guarantees, establishing nonasymptotic error bounds for both score estimation at O(d^{5/2} n^{-2/(k+5)}) and generated distribution at O(d^{5/4} n^{-1/2(k+5)}), primarily driven by the intrinsic factor dimension k rather than the number of assets d, surpassing the dimension-dependent limits in the classical nonparametric statistics literature and making the framework viable for markets with thousands of assets. Numerical studies confirm superior performance in latent subspace recovery under small data regimes. Empirical analysis demonstrates the economic significance of our framework in constructing mean-variance optimal portfolios and factor portfolios. This work presents the first theoretical integration of factor structure with diffusion models, offering a principled approach for high-dimensional financial simulation with limited data.
Stochastic Control for Fine-tuning Diffusion Models: Optimality, Regularity, and Convergence
Dec 24, 2024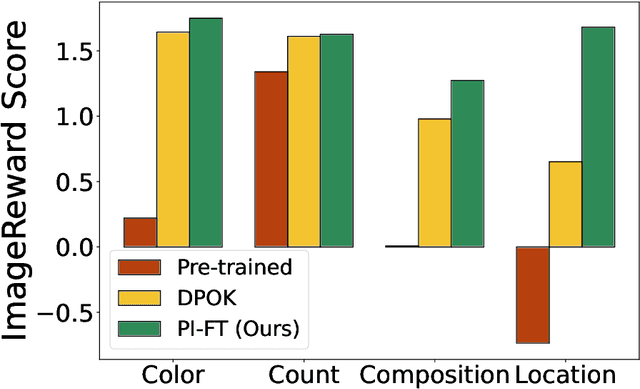

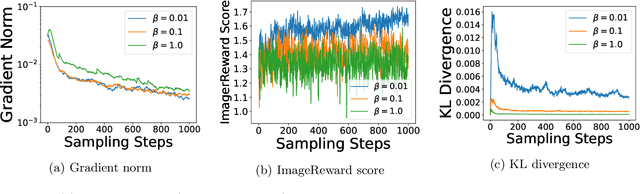

Abstract:Diffusion models have emerged as powerful tools for generative modeling, demonstrating exceptional capability in capturing target data distributions from large datasets. However, fine-tuning these massive models for specific downstream tasks, constraints, and human preferences remains a critical challenge. While recent advances have leveraged reinforcement learning algorithms to tackle this problem, much of the progress has been empirical, with limited theoretical understanding. To bridge this gap, we propose a stochastic control framework for fine-tuning diffusion models. Building on denoising diffusion probabilistic models as the pre-trained reference dynamics, our approach integrates linear dynamics control with Kullback-Leibler regularization. We establish the well-posedness and regularity of the stochastic control problem and develop a policy iteration algorithm (PI-FT) for numerical solution. We show that PI-FT achieves global convergence at a linear rate. Unlike existing work that assumes regularities throughout training, we prove that the control and value sequences generated by the algorithm maintain the regularity. Additionally, we explore extensions of our framework to parametric settings and continuous-time formulations.
Multi-Task Dynamic Pricing in Credit Market with Contextual Information
Oct 18, 2024



Abstract:We study the dynamic pricing problem faced by a broker that buys and sells a large number of financial securities in the credit market, such as corporate bonds, government bonds, loans, and other credit-related securities. One challenge in pricing these securities is their infrequent trading, which leads to insufficient data for individual pricing. However, many of these securities share structural features that can be utilized. Building on this, we propose a multi-task dynamic pricing framework that leverages these shared structures across securities, enhancing pricing accuracy through learning. In our framework, a security is fully characterized by a $d$ dimensional contextual/feature vector. The customer will buy (sell) the security from the broker if the broker quotes a price lower (higher) than that of the competitors. We assume a linear contextual model for the competitor's pricing, with unknown parameters a prior. The parameters for pricing different securities may or may not be similar to each other. The firm's objective is to minimize the expected regret, namely, the expected revenue loss against a clairvoyant policy which has the knowledge of the parameters of the competitor's pricing model. We show that the regret of our policy is better than both a policy that treats each security individually and a policy that treats all securities as the same. Moreover, the regret is bounded by $\tilde{O} ( \delta_{\max} \sqrt{T M d} + M d ) $, where $M$ is the number of securities and $\delta_{\max}$ characterizes the overall dissimilarity across securities in the basket.
Exploratory Optimal Stopping: A Singular Control Formulation
Aug 18, 2024Abstract:This paper explores continuous-time and state-space optimal stopping problems from a reinforcement learning perspective. We begin by formulating the stopping problem using randomized stopping times, where the decision maker's control is represented by the probability of stopping within a given time--specifically, a bounded, non-decreasing, c\`adl\`ag control process. To encourage exploration and facilitate learning, we introduce a regularized version of the problem by penalizing it with the cumulative residual entropy of the randomized stopping time. The regularized problem takes the form of an (n+1)-dimensional degenerate singular stochastic control with finite-fuel. We address this through the dynamic programming principle, which enables us to identify the unique optimal exploratory strategy. For the specific case of a real option problem, we derive a semi-explicit solution to the regularized problem, allowing us to assess the impact of entropy regularization and analyze the vanishing entropy limit. Finally, we propose a reinforcement learning algorithm based on policy iteration. We show both policy improvement and policy convergence results for our proposed algorithm.
Inference of Utilities and Time Preference in Sequential Decision-Making
May 24, 2024



Abstract:This paper introduces a novel stochastic control framework to enhance the capabilities of automated investment managers, or robo-advisors, by accurately inferring clients' investment preferences from past activities. Our approach leverages a continuous-time model that incorporates utility functions and a generic discounting scheme of a time-varying rate, tailored to each client's risk tolerance, valuation of daily consumption, and significant life goals. We address the resulting time inconsistency issue through state augmentation and the establishment of the dynamic programming principle and the verification theorem. Additionally, we provide sufficient conditions for the identifiability of client investment preferences. To complement our theoretical developments, we propose a learning algorithm based on maximum likelihood estimation within a discrete-time Markov Decision Process framework, augmented with entropy regularization. We prove that the log-likelihood function is locally concave, facilitating the fast convergence of our proposed algorithm. Practical effectiveness and efficiency are showcased through two numerical examples, including Merton's problem and an investment problem with unhedgeable risks. Our proposed framework not only advances financial technology by improving personalized investment advice but also contributes broadly to other fields such as healthcare, economics, and artificial intelligence, where understanding individual preferences is crucial.
Neural Network-Based Score Estimation in Diffusion Models: Optimization and Generalization
Feb 06, 2024Abstract:Diffusion models have emerged as a powerful tool rivaling GANs in generating high-quality samples with improved fidelity, flexibility, and robustness. A key component of these models is to learn the score function through score matching. Despite empirical success on various tasks, it remains unclear whether gradient-based algorithms can learn the score function with a provable accuracy. As a first step toward answering this question, this paper establishes a mathematical framework for analyzing score estimation using neural networks trained by gradient descent. Our analysis covers both the optimization and the generalization aspects of the learning procedure. In particular, we propose a parametric form to formulate the denoising score-matching problem as a regression with noisy labels. Compared to the standard supervised learning setup, the score-matching problem introduces distinct challenges, including unbounded input, vector-valued output, and an additional time variable, preventing existing techniques from being applied directly. In this paper, we show that with a properly designed neural network architecture, the score function can be accurately approximated by a reproducing kernel Hilbert space induced by neural tangent kernels. Furthermore, by applying an early-stopping rule for gradient descent and leveraging certain coupling arguments between neural network training and kernel regression, we establish the first generalization error (sample complexity) bounds for learning the score function despite the presence of noise in the observations. Our analysis is grounded in a novel parametric form of the neural network and an innovative connection between score matching and regression analysis, facilitating the application of advanced statistical and optimization techniques.
Fast Policy Learning for Linear Quadratic Control with Entropy Regularization
Dec 03, 2023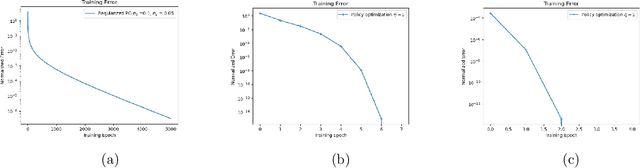
Abstract:This paper proposes and analyzes two new policy learning methods: regularized policy gradient (RPG) and iterative policy optimization (IPO), for a class of discounted linear-quadratic control (LQC) problems over an infinite time horizon with entropy regularization. Assuming access to the exact policy evaluation, both proposed approaches are proven to converge linearly in finding optimal policies of the regularized LQC. Moreover, the IPO method can achieve a super-linear convergence rate once it enters a local region around the optimal policy. Finally, when the optimal policy for an RL problem with a known environment is appropriately transferred as the initial policy to an RL problem with an unknown environment, the IPO method is shown to enable a super-linear convergence rate if the two environments are sufficiently close. Performances of these proposed algorithms are supported by numerical examples.
Risk-sensitive Markov Decision Process and Learning under General Utility Functions
Nov 22, 2023Abstract:Reinforcement Learning (RL) has gained substantial attention across diverse application domains and theoretical investigations. Existing literature on RL theory largely focuses on risk-neutral settings where the decision-maker learns to maximize the expected cumulative reward. However, in practical scenarios such as portfolio management and e-commerce recommendations, decision-makers often persist in heterogeneous risk preferences subject to outcome uncertainties, which can not be well-captured by the risk-neural framework. Incorporating these preferences can be approached through utility theory, yet the development of risk-sensitive RL under general utility functions remains an open question for theoretical exploration. In this paper, we consider a scenario where the decision-maker seeks to optimize a general utility function of the cumulative reward in the framework of a Markov decision process (MDP). To facilitate the Dynamic Programming Principle and Bellman equation, we enlarge the state space with an additional dimension that accounts for the cumulative reward. We propose a discretized approximation scheme to the MDP under enlarged state space, which is tractable and key for algorithmic design. We then propose a modified value iteration algorithm that employs an epsilon-covering over the space of cumulative reward. When a simulator is accessible, our algorithm efficiently learns a near-optimal policy with guaranteed sample complexity. In the absence of a simulator, our algorithm, designed with an upper-confidence-bound exploration approach, identifies a near-optimal policy while ensuring a guaranteed regret bound. For both algorithms, we match the theoretical lower bounds for the risk-neutral setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge