Asymptotic Analysis of Deep Residual Networks

We investigate the asymptotic properties of deep Residual networks (ResNets) as the number of layers increases. We first show the existence of scaling regimes for trained weights markedly different from those implicitly assumed in the neural ODE literature. We study the convergence of the hidden state dynamics in these scaling regimes, showing that one may obtain an ODE, a stochastic differential equation (SDE) or neither of these. In particular, our findings point to the existence of a diffusive regime in which the deep network limit is described by a class of stochastic differential equations (SDEs). Finally, we derive the corresponding scaling limits for the backpropagation dynamics.

Convergence and Implicit Regularization Properties of Gradient Descent for Deep Residual Networks

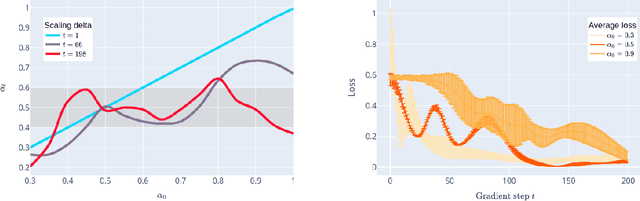
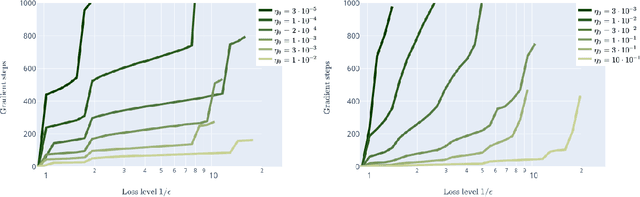
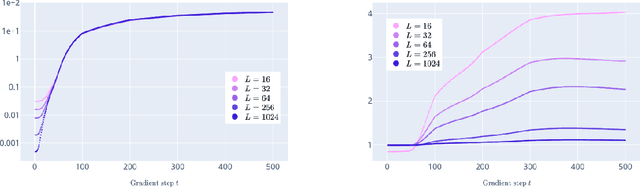
We prove linear convergence of gradient descent to a global minimum for the training of deep residual networks with constant layer width and smooth activation function. We further show that the trained weights, as a function of the layer index, admits a scaling limit which is H\"older continuous as the depth of the network tends to infinity. The proofs are based on non-asymptotic estimates of the loss function and of norms of the network weights along the gradient descent path. We illustrate the relevance of our theoretical results to practical settings using detailed numerical experiments on supervised learning problems.

Scaling Properties of Deep Residual Networks

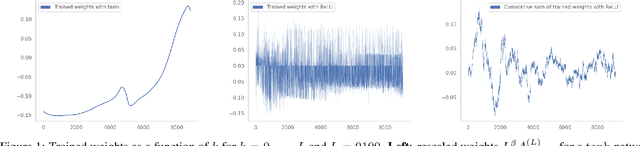
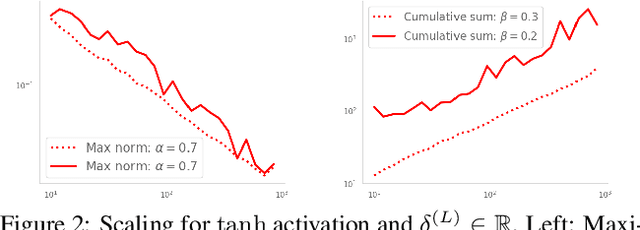
Residual networks (ResNets) have displayed impressive results in pattern recognition and, recently, have garnered considerable theoretical interest due to a perceived link with neural ordinary differential equations (neural ODEs). This link relies on the convergence of network weights to a smooth function as the number of layers increases. We investigate the properties of weights trained by stochastic gradient descent and their scaling with network depth through detailed numerical experiments. We observe the existence of scaling regimes markedly different from those assumed in neural ODE literature. Depending on certain features of the network architecture, such as the smoothness of the activation function, one may obtain an alternative ODE limit, a stochastic differential equation or neither of these. These findings cast doubts on the validity of the neural ODE model as an adequate asymptotic description of deep ResNets and point to an alternative class of differential equations as a better description of the deep network limit.