Yinbin Han
Stochastic Control for Fine-tuning Diffusion Models: Optimality, Regularity, and Convergence
Dec 24, 2024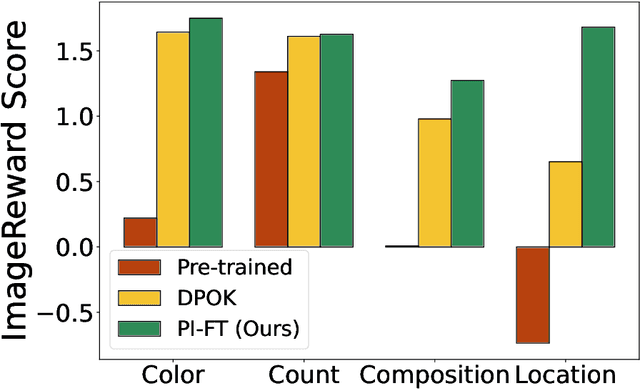

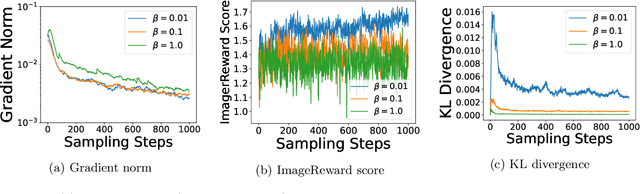

Abstract:Diffusion models have emerged as powerful tools for generative modeling, demonstrating exceptional capability in capturing target data distributions from large datasets. However, fine-tuning these massive models for specific downstream tasks, constraints, and human preferences remains a critical challenge. While recent advances have leveraged reinforcement learning algorithms to tackle this problem, much of the progress has been empirical, with limited theoretical understanding. To bridge this gap, we propose a stochastic control framework for fine-tuning diffusion models. Building on denoising diffusion probabilistic models as the pre-trained reference dynamics, our approach integrates linear dynamics control with Kullback-Leibler regularization. We establish the well-posedness and regularity of the stochastic control problem and develop a policy iteration algorithm (PI-FT) for numerical solution. We show that PI-FT achieves global convergence at a linear rate. Unlike existing work that assumes regularities throughout training, we prove that the control and value sequences generated by the algorithm maintain the regularity. Additionally, we explore extensions of our framework to parametric settings and continuous-time formulations.
Neural Network-Based Score Estimation in Diffusion Models: Optimization and Generalization
Feb 06, 2024Abstract:Diffusion models have emerged as a powerful tool rivaling GANs in generating high-quality samples with improved fidelity, flexibility, and robustness. A key component of these models is to learn the score function through score matching. Despite empirical success on various tasks, it remains unclear whether gradient-based algorithms can learn the score function with a provable accuracy. As a first step toward answering this question, this paper establishes a mathematical framework for analyzing score estimation using neural networks trained by gradient descent. Our analysis covers both the optimization and the generalization aspects of the learning procedure. In particular, we propose a parametric form to formulate the denoising score-matching problem as a regression with noisy labels. Compared to the standard supervised learning setup, the score-matching problem introduces distinct challenges, including unbounded input, vector-valued output, and an additional time variable, preventing existing techniques from being applied directly. In this paper, we show that with a properly designed neural network architecture, the score function can be accurately approximated by a reproducing kernel Hilbert space induced by neural tangent kernels. Furthermore, by applying an early-stopping rule for gradient descent and leveraging certain coupling arguments between neural network training and kernel regression, we establish the first generalization error (sample complexity) bounds for learning the score function despite the presence of noise in the observations. Our analysis is grounded in a novel parametric form of the neural network and an innovative connection between score matching and regression analysis, facilitating the application of advanced statistical and optimization techniques.
Policy Gradient Converges to the Globally Optimal Policy for Nearly Linear-Quadratic Regulators
Mar 23, 2023Abstract:Nonlinear control systems with partial information to the decision maker are prevalent in a variety of applications. As a step toward studying such nonlinear systems, this work explores reinforcement learning methods for finding the optimal policy in the nearly linear-quadratic regulator systems. In particular, we consider a dynamic system that combines linear and nonlinear components, and is governed by a policy with the same structure. Assuming that the nonlinear component comprises kernels with small Lipschitz coefficients, we characterize the optimization landscape of the cost function. Although the cost function is nonconvex in general, we establish the local strong convexity and smoothness in the vicinity of the global optimizer. Additionally, we propose an initialization mechanism to leverage these properties. Building on the developments, we design a policy gradient algorithm that is guaranteed to converge to the globally optimal policy with a linear rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge