Inference of Utilities and Time Preference in Sequential Decision-Making

This paper introduces a novel stochastic control framework to enhance the capabilities of automated investment managers, or robo-advisors, by accurately inferring clients' investment preferences from past activities. Our approach leverages a continuous-time model that incorporates utility functions and a generic discounting scheme of a time-varying rate, tailored to each client's risk tolerance, valuation of daily consumption, and significant life goals. We address the resulting time inconsistency issue through state augmentation and the establishment of the dynamic programming principle and the verification theorem. Additionally, we provide sufficient conditions for the identifiability of client investment preferences. To complement our theoretical developments, we propose a learning algorithm based on maximum likelihood estimation within a discrete-time Markov Decision Process framework, augmented with entropy regularization. We prove that the log-likelihood function is locally concave, facilitating the fast convergence of our proposed algorithm. Practical effectiveness and efficiency are showcased through two numerical examples, including Merton's problem and an investment problem with unhedgeable risks. Our proposed framework not only advances financial technology by improving personalized investment advice but also contributes broadly to other fields such as healthcare, economics, and artificial intelligence, where understanding individual preferences is crucial.

Risk of Transfer Learning and its Applications in Finance

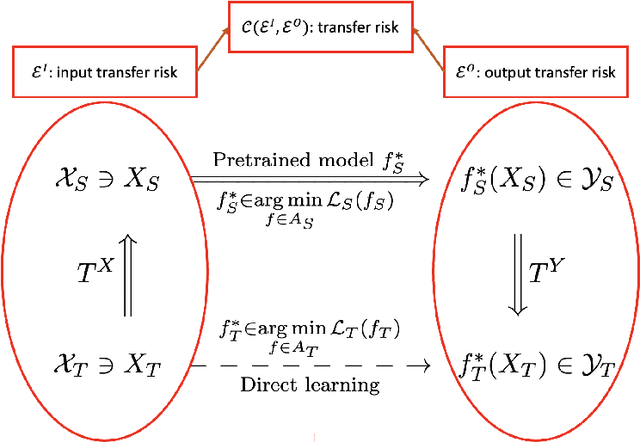
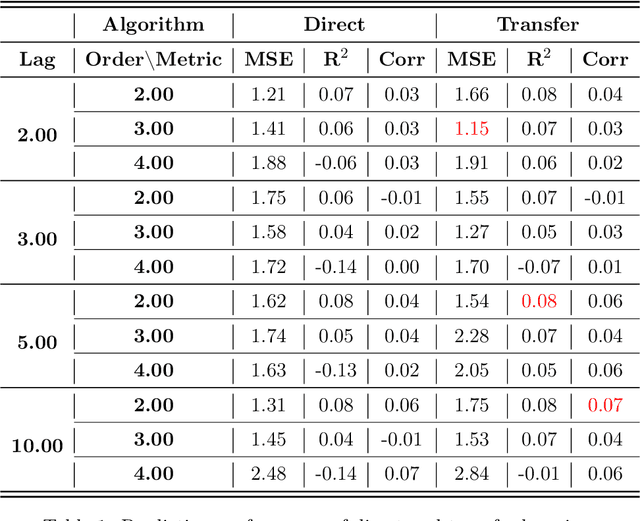
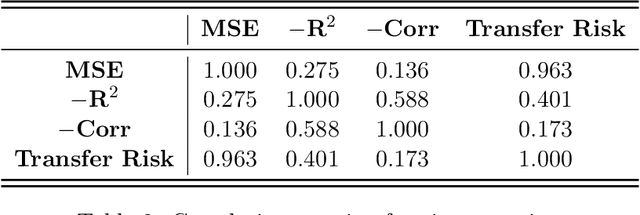
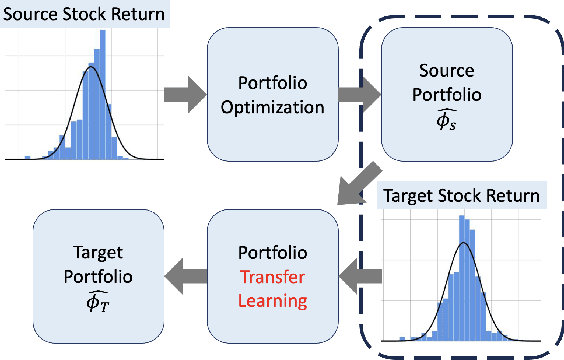
Transfer learning is an emerging and popular paradigm for utilizing existing knowledge from previous learning tasks to improve the performance of new ones. In this paper, we propose a novel concept of transfer risk and and analyze its properties to evaluate transferability of transfer learning. We apply transfer learning techniques and this concept of transfer risk to stock return prediction and portfolio optimization problems. Numerical results demonstrate a strong correlation between transfer risk and overall transfer learning performance, where transfer risk provides a computationally efficient way to identify appropriate source tasks in transfer learning, including cross-continent, cross-sector, and cross-frequency transfer for portfolio optimization.

Transfer Learning for Portfolio Optimization

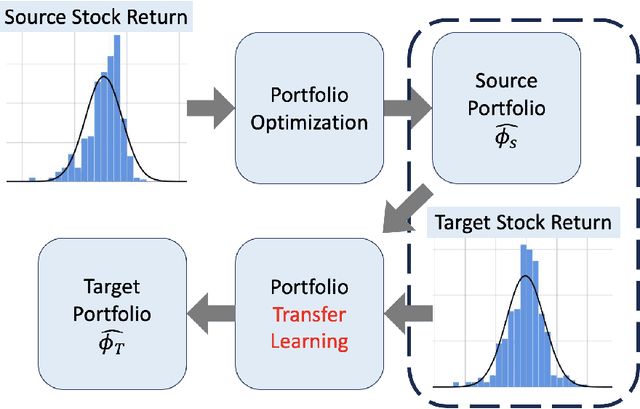
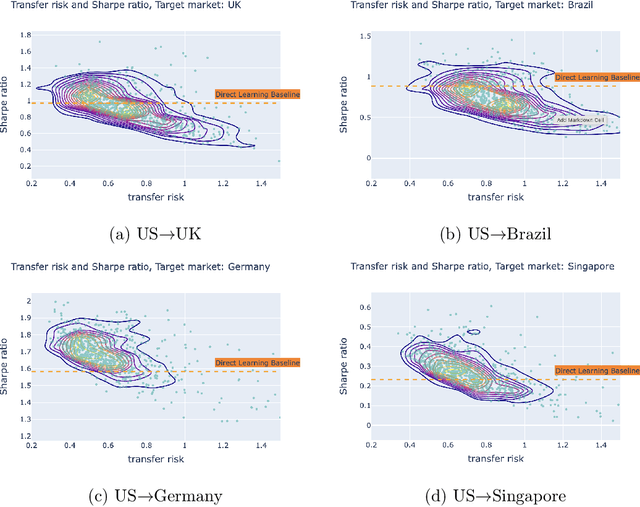
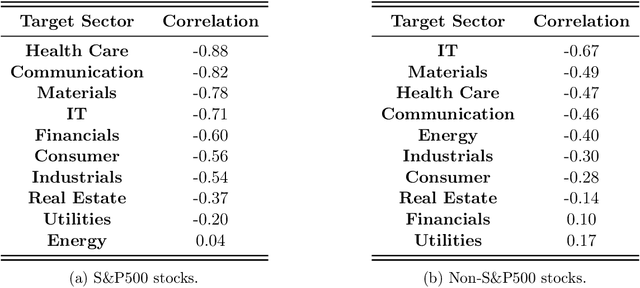
In this work, we explore the possibility of utilizing transfer learning techniques to address the financial portfolio optimization problem. We introduce a novel concept called "transfer risk", within the optimization framework of transfer learning. A series of numerical experiments are conducted from three categories: cross-continent transfer, cross-sector transfer, and cross-frequency transfer. In particular, 1. a strong correlation between the transfer risk and the overall performance of transfer learning methods is established, underscoring the significance of transfer risk as a viable indicator of "transferability"; 2. transfer risk is shown to provide a computationally efficient way to identify appropriate source tasks in transfer learning, enhancing the efficiency and effectiveness of the transfer learning approach; 3. additionally, the numerical experiments offer valuable new insights for portfolio management across these different settings.

Feasibility of Transfer Learning: A Mathematical Framework

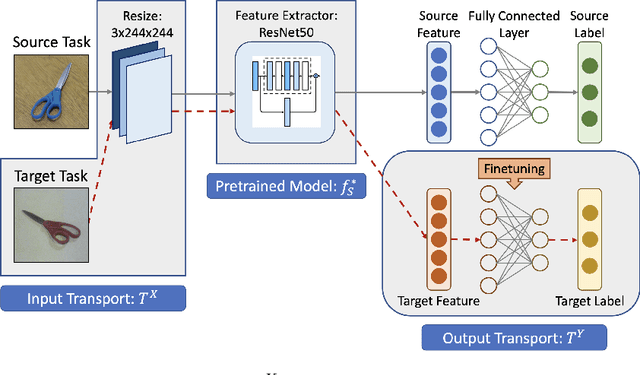
Transfer learning is a popular paradigm for utilizing existing knowledge from previous learning tasks to improve the performance of new ones. It has enjoyed numerous empirical successes and inspired a growing number of theoretical studies. This paper addresses the feasibility issue of transfer learning. It begins by establishing the necessary mathematical concepts and constructing a mathematical framework for transfer learning. It then identifies and formulates the three-step transfer learning procedure as an optimization problem, allowing for the resolution of the feasibility issue. Importantly, it demonstrates that under certain technical conditions, such as appropriate choice of loss functions and data sets, an optimal procedure for transfer learning exists. This study of the feasibility issue brings additional insights into various transfer learning problems. It sheds light on the impact of feature augmentation on model performance, explores potential extensions of domain adaptation, and examines the feasibility of efficient feature extractor transfer in image classification.

Feasibility and Transferability of Transfer Learning: A Mathematical Framework

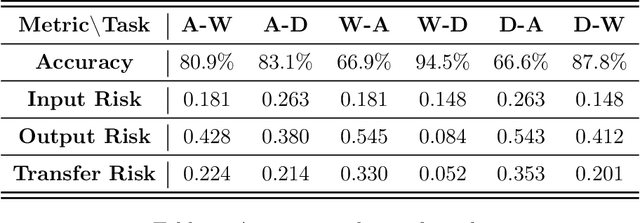
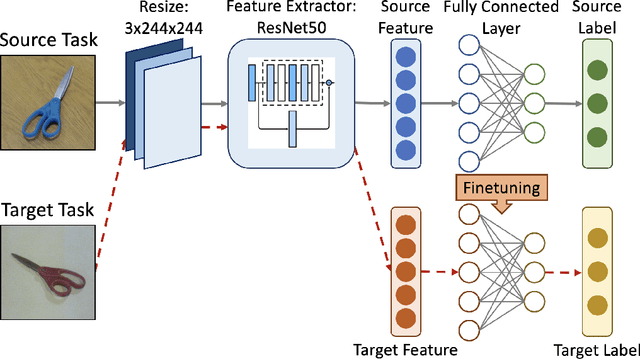
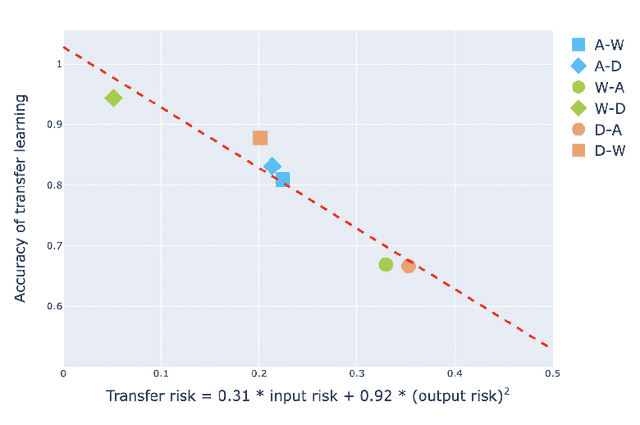
Transfer learning is an emerging and popular paradigm for utilizing existing knowledge from previous learning tasks to improve the performance of new ones. Despite its numerous empirical successes, theoretical analysis for transfer learning is limited. In this paper we build for the first time, to the best of our knowledge, a mathematical framework for the general procedure of transfer learning. Our unique reformulation of transfer learning as an optimization problem allows for the first time, analysis of its feasibility. Additionally, we propose a novel concept of transfer risk to evaluate transferability of transfer learning. Our numerical studies using the Office-31 dataset demonstrate the potential and benefits of incorporating transfer risk in the evaluation of transfer learning performance.

Towards mapping the contemporary art world with ArtLM: an art-specific NLP model

With an increasing amount of data in the art world, discovering artists and artworks suitable to collectors' tastes becomes a challenge. It is no longer enough to use visual information, as contextual information about the artist has become just as important in contemporary art. In this work, we present a generic Natural Language Processing framework (called ArtLM) to discover the connections among contemporary artists based on their biographies. In this approach, we first continue to pre-train the existing general English language models with a large amount of unlabelled art-related data. We then fine-tune this new pre-trained model with our biography pair dataset manually annotated by a team of professionals in the art industry. With extensive experiments, we demonstrate that our ArtLM achieves 85.6% accuracy and 84.0% F1 score and outperforms other baseline models. We also provide a visualisation and a qualitative analysis of the artist network built from ArtLM's outputs.

Meta-learning with GANs for anomaly detection, with deployment in high-speed rail inspection system

Anomaly detection has been an active research area with a wide range of potential applications. Key challenges for anomaly detection in the AI era with big data include lack of prior knowledge of potential anomaly types, highly complex and noisy background in input data, scarce abnormal samples, and imbalanced training dataset. In this work, we propose a meta-learning framework for anomaly detection to deal with these issues. Within this framework, we incorporate the idea of generative adversarial networks (GANs) with appropriate choices of loss functions including structural similarity index measure (SSIM). Experiments with limited labeled data for high-speed rail inspection demonstrate that our meta-learning framework is sharp and robust in identifying anomalies. Our framework has been deployed in five high-speed railways of China since 2021: it has reduced more than 99.7% workload and saved 96.7% inspection time.

Identifiability in inverse reinforcement learning

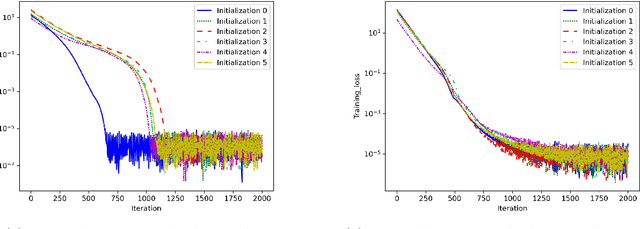
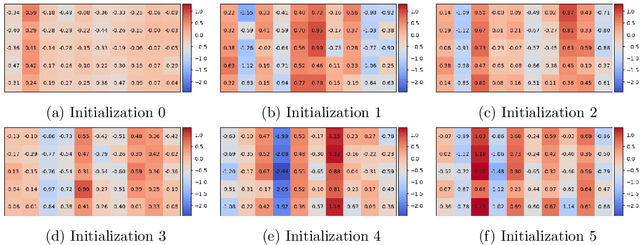
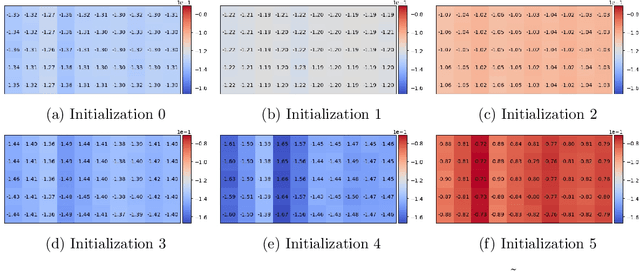
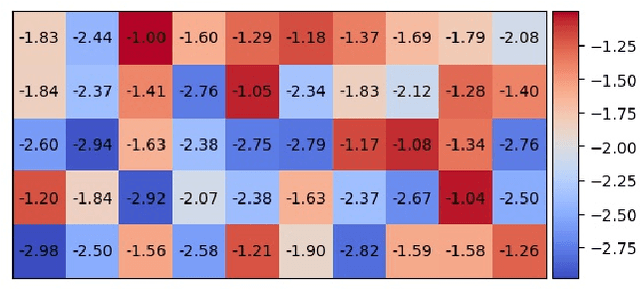
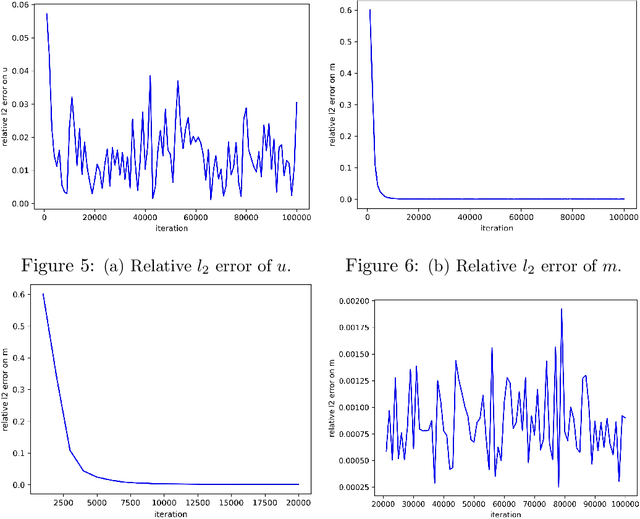
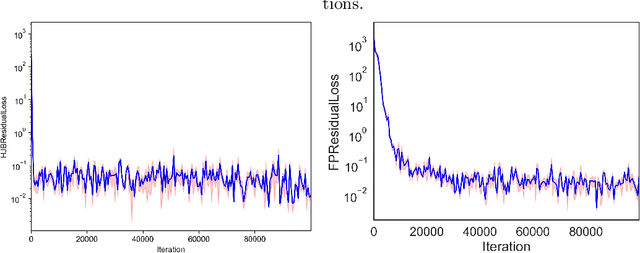
Inverse reinforcement learning attempts to reconstruct the reward function in a Markov decision problem, using observations of agent actions. As already observed by Russell the problem is ill-posed, and the reward function is not identifiable, even under the presence of perfect information about optimal behavior. We provide a resolution to this non-identifiability for problems with entropy regularization. For a given environment, we fully characterize the reward functions leading to a given policy and demonstrate that, given demonstrations of actions for the same reward under two distinct discount factors, or under sufficiently different environments, the unobserved reward can be recovered up to a constant. Through a simple numerical experiment, we demonstrate the accurate reconstruction of the reward function through our proposed resolution.

Generative Adversarial Network: Some Analytical Perspectives

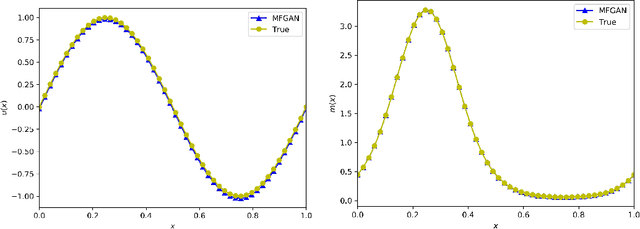
Ever since its debut, generative adversarial networks (GANs) have attracted tremendous amount of attention. Over the past years, different variations of GANs models have been developed and tailored to different applications in practice. Meanwhile, some issues regarding the performance and training of GANs have been noticed and investigated from various theoretical perspectives. This subchapter will start from an introduction of GANs from an analytical perspective, then move on the training of GANs via SDE approximations and finally discuss some applications of GANs in computing high dimensional MFGs as well as tackling mathematical finance problems.

Approximation and convergence of GANs training: an SDE approach

Generative adversarial networks (GANs) have enjoyed tremendous empirical successes, and research interest in the theoretical understanding of GANs training process is rapidly growing, especially for its evolution and convergence analysis. This paper establishes approximations, with precise error bound analysis, for the training of GANs under stochastic gradient algorithms (SGAs). The approximations are in the form of coupled stochastic differential equations (SDEs). The analysis of the SDEs and the associated invariant measures yields conditions for the convergence of GANs training. Further analysis of the invariant measure for the coupled SDEs gives rise to a fluctuation-dissipation relations (FDRs) for GANs, revealing the trade-off of the loss landscape between the generator and the discriminator and providing guidance for learning rate scheduling.