Feasibility of Transfer Learning: A Mathematical Framework
Paper and Code
May 22, 2023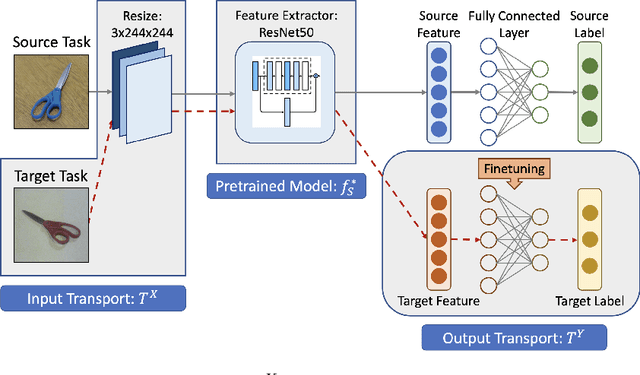
Transfer learning is a popular paradigm for utilizing existing knowledge from previous learning tasks to improve the performance of new ones. It has enjoyed numerous empirical successes and inspired a growing number of theoretical studies. This paper addresses the feasibility issue of transfer learning. It begins by establishing the necessary mathematical concepts and constructing a mathematical framework for transfer learning. It then identifies and formulates the three-step transfer learning procedure as an optimization problem, allowing for the resolution of the feasibility issue. Importantly, it demonstrates that under certain technical conditions, such as appropriate choice of loss functions and data sets, an optimal procedure for transfer learning exists. This study of the feasibility issue brings additional insights into various transfer learning problems. It sheds light on the impact of feature augmentation on model performance, explores potential extensions of domain adaptation, and examines the feasibility of efficient feature extractor transfer in image classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge