Adel Javanmard
Accelerating Scientific Research with Gemini: Case Studies and Common Techniques
Feb 03, 2026Abstract:Recent advances in large language models (LLMs) have opened new avenues for accelerating scientific research. While models are increasingly capable of assisting with routine tasks, their ability to contribute to novel, expert-level mathematical discovery is less understood. We present a collection of case studies demonstrating how researchers have successfully collaborated with advanced AI models, specifically Google's Gemini-based models (in particular Gemini Deep Think and its advanced variants), to solve open problems, refute conjectures, and generate new proofs across diverse areas in theoretical computer science, as well as other areas such as economics, optimization, and physics. Based on these experiences, we extract common techniques for effective human-AI collaboration in theoretical research, such as iterative refinement, problem decomposition, and cross-disciplinary knowledge transfer. While the majority of our results stem from this interactive, conversational methodology, we also highlight specific instances that push beyond standard chat interfaces. These include deploying the model as a rigorous adversarial reviewer to detect subtle flaws in existing proofs, and embedding it within a "neuro-symbolic" loop that autonomously writes and executes code to verify complex derivations. Together, these examples highlight the potential of AI not just as a tool for automation, but as a versatile, genuine partner in the creative process of scientific discovery.
Differentially Private Model-X Knockoffs via Johnson-Lindenstrauss Transform
Aug 06, 2025Abstract:We introduce a novel privatization framework for high-dimensional controlled variable selection. Our framework enables rigorous False Discovery Rate (FDR) control under differential privacy constraints. While the Model-X knockoff procedure provides FDR guarantees by constructing provably exchangeable ``negative control" features, existing privacy mechanisms like Laplace or Gaussian noise injection disrupt its core exchangeability conditions. Our key innovation lies in privatizing the data knockoff matrix through the Gaussian Johnson-Lindenstrauss Transformation (JLT), a dimension reduction technique that simultaneously preserves covariate relationships through approximate isometry for $(\epsilon,\delta)$-differential privacy. We theoretically characterize both FDR and the power of the proposed private variable selection procedure, in an asymptotic regime. Our theoretical analysis characterizes the role of different factors, such as the JLT's dimension reduction ratio, signal-to-noise ratio, differential privacy parameters, sample size and feature dimension, in shaping the privacy-power trade-off. Our analysis is based on a novel `debiasing technique' for high-dimensional private knockoff procedure. We further establish sufficient conditions under which the power of the proposed procedure converges to one. This work bridges two critical paradigms -- knockoff-based FDR control and private data release -- enabling reliable variable selection in sensitive domains. Our analysis demonstrates that structural privacy preservation through random projections outperforms the classical noise addition mechanism, maintaining statistical power even under strict privacy budgets.
Self-Boost via Optimal Retraining: An Analysis via Approximate Message Passing
May 21, 2025Abstract:Retraining a model using its own predictions together with the original, potentially noisy labels is a well-known strategy for improving the model performance. While prior works have demonstrated the benefits of specific heuristic retraining schemes, the question of how to optimally combine the model's predictions and the provided labels remains largely open. This paper addresses this fundamental question for binary classification tasks. We develop a principled framework based on approximate message passing (AMP) to analyze iterative retraining procedures for two ground truth settings: Gaussian mixture model (GMM) and generalized linear model (GLM). Our main contribution is the derivation of the Bayes optimal aggregator function to combine the current model's predictions and the given labels, which when used to retrain the same model, minimizes its prediction error. We also quantify the performance of this optimal retraining strategy over multiple rounds. We complement our theoretical results by proposing a practically usable version of the theoretically-optimal aggregator function for linear probing with the cross-entropy loss, and demonstrate its superiority over baseline methods in the high label noise regime.
DeepCrossAttention: Supercharging Transformer Residual Connections
Feb 10, 2025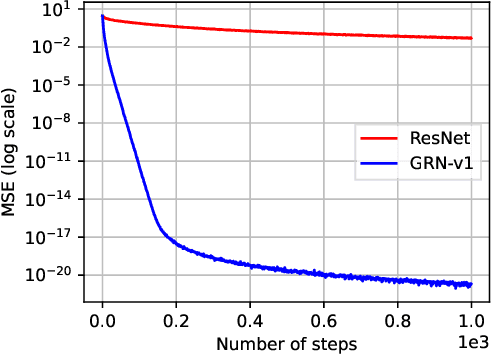
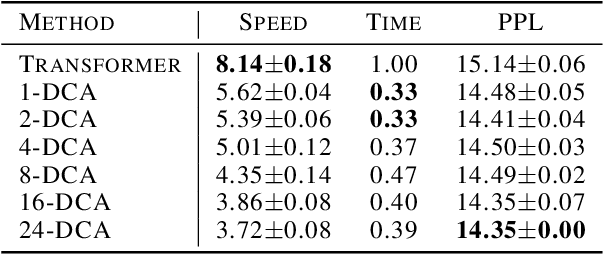
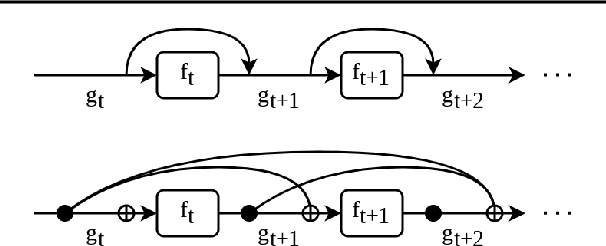
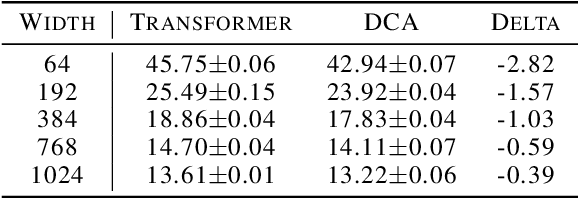
Abstract:Transformer networks have achieved remarkable success across diverse domains, leveraging a variety of architectural innovations, including residual connections. However, traditional residual connections, which simply sum the outputs of previous layers, can dilute crucial information. This work introduces DeepCrossAttention (DCA), an approach that enhances residual learning in transformers. DCA employs learnable, input-dependent weights to dynamically combine layer outputs, enabling the model to selectively focus on the most relevant information in any of the previous layers. Furthermore, DCA incorporates depth-wise cross-attention, allowing for richer interactions between layers at different depths. Our language modeling experiments show that DCA achieves improved perplexity for a given training time. Moreover, DCA obtains the same model quality up to 3x faster while adding a negligible number of parameters. Theoretical analysis confirms that DCA provides an improved trade-off between accuracy and model size when the ratio of collective layer ranks to the ambient dimension falls below a critical threshold.
Robust Feature Learning for Multi-Index Models in High Dimensions
Oct 21, 2024
Abstract:Recently, there have been numerous studies on feature learning with neural networks, specifically on learning single- and multi-index models where the target is a function of a low-dimensional projection of the input. Prior works have shown that in high dimensions, the majority of the compute and data resources are spent on recovering the low-dimensional projection; once this subspace is recovered, the remainder of the target can be learned independently of the ambient dimension. However, implications of feature learning in adversarial settings remain unexplored. In this work, we take the first steps towards understanding adversarially robust feature learning with neural networks. Specifically, we prove that the hidden directions of a multi-index model offer a Bayes optimal low-dimensional projection for robustness against $\ell_2$-bounded adversarial perturbations under the squared loss, assuming that the multi-index coordinates are statistically independent from the rest of the coordinates. Therefore, robust learning can be achieved by first performing standard feature learning, then robustly tuning a linear readout layer on top of the standard representations. In particular, we show that adversarially robust learning is just as easy as standard learning, in the sense that the additional number of samples needed to robustly learn multi-index models when compared to standard learning, does not depend on dimensionality.
Multi-Task Dynamic Pricing in Credit Market with Contextual Information
Oct 18, 2024



Abstract:We study the dynamic pricing problem faced by a broker that buys and sells a large number of financial securities in the credit market, such as corporate bonds, government bonds, loans, and other credit-related securities. One challenge in pricing these securities is their infrequent trading, which leads to insufficient data for individual pricing. However, many of these securities share structural features that can be utilized. Building on this, we propose a multi-task dynamic pricing framework that leverages these shared structures across securities, enhancing pricing accuracy through learning. In our framework, a security is fully characterized by a $d$ dimensional contextual/feature vector. The customer will buy (sell) the security from the broker if the broker quotes a price lower (higher) than that of the competitors. We assume a linear contextual model for the competitor's pricing, with unknown parameters a prior. The parameters for pricing different securities may or may not be similar to each other. The firm's objective is to minimize the expected regret, namely, the expected revenue loss against a clairvoyant policy which has the knowledge of the parameters of the competitor's pricing model. We show that the regret of our policy is better than both a policy that treats each security individually and a policy that treats all securities as the same. Moreover, the regret is bounded by $\tilde{O} ( \delta_{\max} \sqrt{T M d} + M d ) $, where $M$ is the number of securities and $\delta_{\max}$ characterizes the overall dissimilarity across securities in the basket.
Retraining with Predicted Hard Labels Provably Increases Model Accuracy
Jun 17, 2024Abstract:The performance of a model trained with \textit{noisy labels} is often improved by simply \textit{retraining} the model with its own predicted \textit{hard} labels (i.e., $1$/$0$ labels). Yet, a detailed theoretical characterization of this phenomenon is lacking. In this paper, we theoretically analyze retraining in a linearly separable setting with randomly corrupted labels given to us and prove that retraining can improve the population accuracy obtained by initially training with the given (noisy) labels. To the best of our knowledge, this is the first such theoretical result. Retraining finds application in improving training with label differential privacy (DP) which involves training with noisy labels. We empirically show that retraining selectively on the samples for which the predicted label matches the given label significantly improves label DP training at \textit{no extra privacy cost}; we call this \textit{consensus-based retraining}. For e.g., when training ResNet-18 on CIFAR-100 with $\epsilon=3$ label DP, we obtain $6.4\%$ improvement in accuracy with consensus-based retraining.
Optimistic Rates for Learning from Label Proportions
Jun 01, 2024Abstract:We consider a weakly supervised learning problem called Learning from Label Proportions (LLP), where examples are grouped into ``bags'' and only the average label within each bag is revealed to the learner. We study various learning rules for LLP that achieve PAC learning guarantees for classification loss. We establish that the classical Empirical Proportional Risk Minimization (EPRM) learning rule (Yu et al., 2014) achieves fast rates under realizability, but EPRM and similar proportion matching learning rules can fail in the agnostic setting. We also show that (1) a debiased proportional square loss, as well as (2) a recently proposed EasyLLP learning rule (Busa-Fekete et al., 2023) both achieve ``optimistic rates'' (Panchenko, 2002); in both the realizable and agnostic settings, their sample complexity is optimal (up to log factors) in terms of $\epsilon, \delta$, and VC dimension.
PriorBoost: An Adaptive Algorithm for Learning from Aggregate Responses
Feb 07, 2024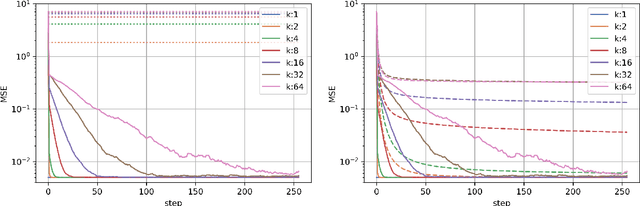
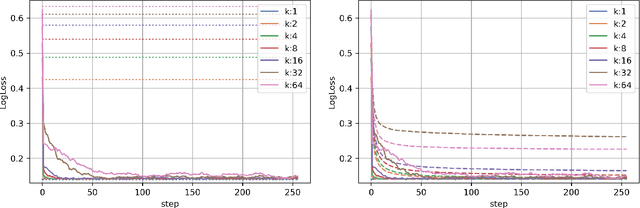
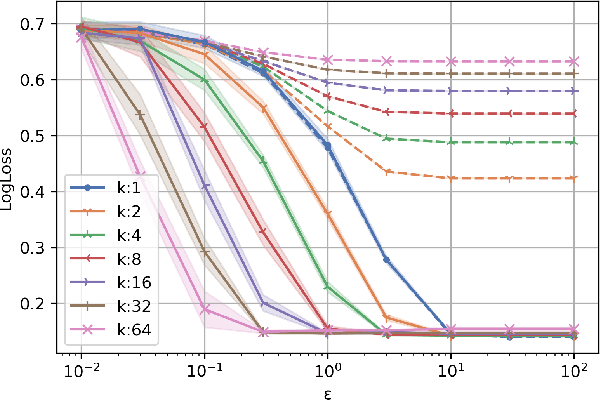
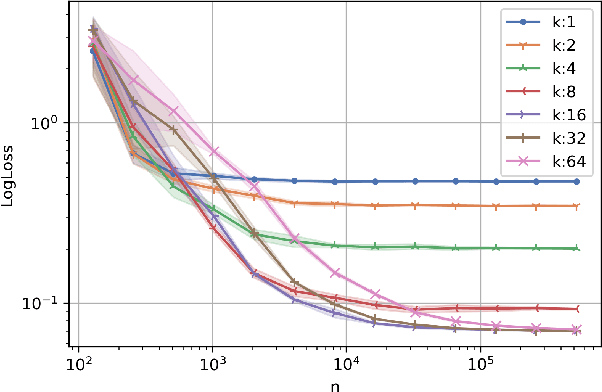
Abstract:This work studies algorithms for learning from aggregate responses. We focus on the construction of aggregation sets (called bags in the literature) for event-level loss functions. We prove for linear regression and generalized linear models (GLMs) that the optimal bagging problem reduces to one-dimensional size-constrained $k$-means clustering. Further, we theoretically quantify the advantage of using curated bags over random bags. We then propose the PriorBoost algorithm, which adaptively forms bags of samples that are increasingly homogeneous with respect to (unobserved) individual responses to improve model quality. We study label differential privacy for aggregate learning, and we also provide extensive experiments showing that PriorBoost regularly achieves optimal model quality for event-level predictions, in stark contrast to non-adaptive algorithms.
Learning from Aggregate responses: Instance Level versus Bag Level Loss Functions
Jan 20, 2024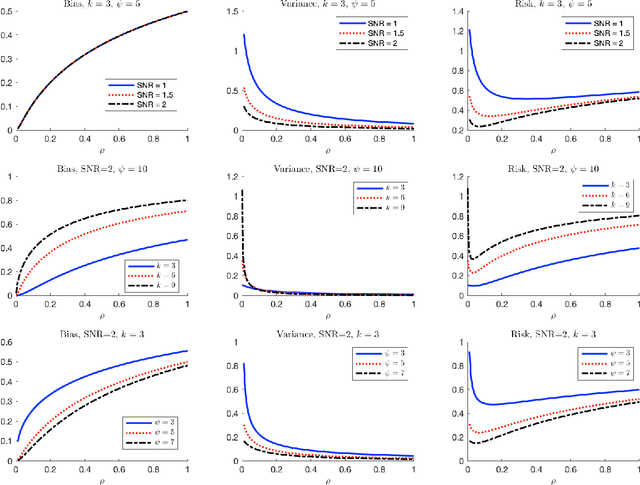
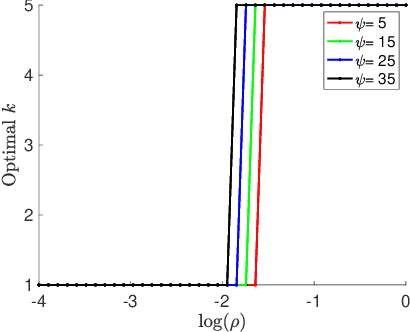
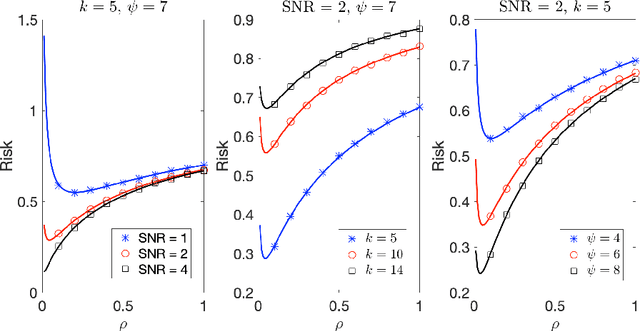
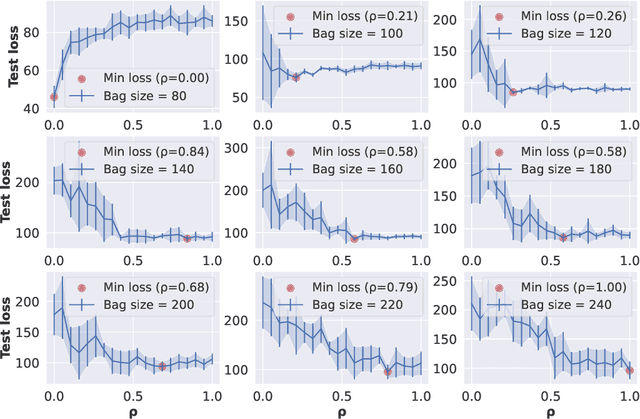
Abstract:Due to the rise of privacy concerns, in many practical applications the training data is aggregated before being shared with the learner, in order to protect privacy of users' sensitive responses. In an aggregate learning framework, the dataset is grouped into bags of samples, where each bag is available only with an aggregate response, providing a summary of individuals' responses in that bag. In this paper, we study two natural loss functions for learning from aggregate responses: bag-level loss and the instance-level loss. In the former, the model is learnt by minimizing a loss between aggregate responses and aggregate model predictions, while in the latter the model aims to fit individual predictions to the aggregate responses. In this work, we show that the instance-level loss can be perceived as a regularized form of the bag-level loss. This observation lets us compare the two approaches with respect to bias and variance of the resulting estimators, and introduce a novel interpolating estimator which combines the two approaches. For linear regression tasks, we provide a precise characterization of the risk of the interpolating estimator in an asymptotic regime where the size of the training set grows in proportion to the features dimension. Our analysis allows us to theoretically understand the effect of different factors, such as bag size on the model prediction risk. In addition, we propose a mechanism for differentially private learning from aggregate responses and derive the optimal bag size in terms of prediction risk-privacy trade-off. We also carry out thorough experiments to corroborate our theory and show the efficacy of the interpolating estimator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge