Super Apriel: One Checkpoint, Many Speeds

We release Super Apriel, a 15B-parameter supernet in which every decoder layer provides four trained mixer choices -- Full Attention (FA), Sliding Window Attention (SWA), Kimi Delta Attention (KDA), and Gated DeltaNet (GDN). A placement selects one mixer per layer; placements can be switched between requests at serving time without reloading weights, enabling multiple speed presets from a single checkpoint. The shared checkpoint also enables speculative decoding without a separate draft model. The all-FA preset matches the Apriel 1.6 teacher on all reported benchmarks; recommended hybrid presets span $2.9\times$ to $10.7\times$ decode throughput at 96% to 77% quality retention, with throughput advantages that compound at longer context lengths. With four mixer types across 48 layers, the configuration space is vast. A surrogate that predicts placement quality from the per-layer mixer assignment makes the speed-quality landscape tractable and identifies the best tradeoffs at each speed level. We investigate whether the best configurations at each speed level can be identified early in training or only after convergence. Rankings stabilize quickly at 0.5B scale, but the most efficient configurations exhibit higher instability at 15B, cautioning against extrapolation from smaller models. Super Apriel is trained by stochastic distillation from a frozen Apriel 1.6 teacher, followed by supervised fine-tuning. We release the supernet weights, Fast-LLM training code, vLLM serving code, and a placement optimization toolkit.

On Fitting Flow Models with Large Sinkhorn Couplings

Flow models transform data gradually from one modality (e.g. noise) onto another (e.g. images). Such models are parameterized by a time-dependent velocity field, trained to fit segments connecting pairs of source and target points. When the pairing between source and target points is given, training flow models boils down to a supervised regression problem. When no such pairing exists, as is the case when generating data from noise, training flows is much harder. A popular approach lies in picking source and target points independently. This can, however, lead to velocity fields that are slow to train, but also costly to integrate at inference time. In theory, one would greatly benefit from training flow models by sampling pairs from an optimal transport (OT) measure coupling source and target, since this would lead to a highly efficient flow solving the Benamou and Brenier dynamical OT problem. In practice, recent works have proposed to sample mini-batches of $n$ source and $n$ target points and reorder them using an OT solver to form better pairs. These works have advocated using batches of size $n\approx 256$, and considered OT solvers that return couplings that are either sharp (using e.g. the Hungarian algorithm) or blurred (using e.g. entropic regularization, a.k.a. Sinkhorn). We follow in the footsteps of these works by exploring the benefits of increasing $n$ by three to four orders of magnitude, and look more carefully on the effect of the entropic regularization $\varepsilon$ used in the Sinkhorn algorithm. Our analysis is facilitated by new scale invariant quantities to report the sharpness of a coupling, while our sharded computations across multiple GPU or GPU nodes allow scaling up $n$. We show that in both synthetic and image generation tasks, flow models greatly benefit when fitted with large Sinkhorn couplings, with a low entropic regularization $\varepsilon$.

When Do Transformers Outperform Feedforward and Recurrent Networks? A Statistical Perspective

Theoretical efforts to prove advantages of Transformers in comparison with classical architectures such as feedforward and recurrent neural networks have mostly focused on representational power. In this work, we take an alternative perspective and prove that even with infinite compute, feedforward and recurrent networks may suffer from larger sample complexity compared to Transformers, as the latter can adapt to a form of dynamic sparsity. Specifically, we consider a sequence-to-sequence data generating model on sequences of length $N$, in which the output at each position depends only on $q$ relevant tokens with $q \ll N$, and the positions of these tokens are described in the input prompt. We prove that a single-layer Transformer can learn this model if and only if its number of attention heads is at least $q$, in which case it achieves a sample complexity almost independent of $N$, while recurrent networks require $N^{\Omega(1)}$ samples on the same problem. If we simplify this model, recurrent networks may achieve a complexity almost independent of $N$, while feedforward networks still require $N$ samples. Consequently, our proposed sparse retrieval model illustrates a natural hierarchy in sample complexity across these architectures.

Robust Feature Learning for Multi-Index Models in High Dimensions

Recently, there have been numerous studies on feature learning with neural networks, specifically on learning single- and multi-index models where the target is a function of a low-dimensional projection of the input. Prior works have shown that in high dimensions, the majority of the compute and data resources are spent on recovering the low-dimensional projection; once this subspace is recovered, the remainder of the target can be learned independently of the ambient dimension. However, implications of feature learning in adversarial settings remain unexplored. In this work, we take the first steps towards understanding adversarially robust feature learning with neural networks. Specifically, we prove that the hidden directions of a multi-index model offer a Bayes optimal low-dimensional projection for robustness against $\ell_2$-bounded adversarial perturbations under the squared loss, assuming that the multi-index coordinates are statistically independent from the rest of the coordinates. Therefore, robust learning can be achieved by first performing standard feature learning, then robustly tuning a linear readout layer on top of the standard representations. In particular, we show that adversarially robust learning is just as easy as standard learning, in the sense that the additional number of samples needed to robustly learn multi-index models when compared to standard learning, does not depend on dimensionality.

Learning Multi-Index Models with Neural Networks via Mean-Field Langevin Dynamics

We study the problem of learning multi-index models in high-dimensions using a two-layer neural network trained with the mean-field Langevin algorithm. Under mild distributional assumptions on the data, we characterize the effective dimension $d_{\mathrm{eff}}$ that controls both sample and computational complexity by utilizing the adaptivity of neural networks to latent low-dimensional structures. When the data exhibit such a structure, $d_{\mathrm{eff}}$ can be significantly smaller than the ambient dimension. We prove that the sample complexity grows almost linearly with $d_{\mathrm{eff}}$, bypassing the limitations of the information and generative exponents that appeared in recent analyses of gradient-based feature learning. On the other hand, the computational complexity may inevitably grow exponentially with $d_{\mathrm{eff}}$ in the worst-case scenario. Motivated by improving computational complexity, we take the first steps towards polynomial time convergence of the mean-field Langevin algorithm by investigating a setting where the weights are constrained to be on a compact manifold with positive Ricci curvature, such as the hypersphere. There, we study assumptions under which polynomial time convergence is achievable, whereas similar assumptions in the Euclidean setting lead to exponential time complexity.

Mean-Field Langevin Dynamics for Signed Measures via a Bilevel Approach

Mean-field Langevin dynamics (MLFD) is a class of interacting particle methods that tackle convex optimization over probability measures on a manifold, which are scalable, versatile, and enjoy computational guarantees. However, some important problems -- such as risk minimization for infinite width two-layer neural networks, or sparse deconvolution -- are originally defined over the set of signed, rather than probability, measures. In this paper, we investigate how to extend the MFLD framework to convex optimization problems over signed measures. Among two known reductions from signed to probability measures -- the lifting and the bilevel approaches -- we show that the bilevel reduction leads to stronger guarantees and faster rates (at the price of a higher per-iteration complexity). In particular, we investigate the convergence rate of MFLD applied to the bilevel reduction in the low-noise regime and obtain two results. First, this dynamics is amenable to an annealing schedule, adapted from Suzuki et al. (2023), that results in improved convergence rates to a fixed multiplicative accuracy. Second, we investigate the problem of learning a single neuron with the bilevel approach and obtain local exponential convergence rates that depend polynomially on the dimension and noise level (to compare with the exponential dependence that would result from prior analyses).

A Separation in Heavy-Tailed Sampling: Gaussian vs. Stable Oracles for Proximal Samplers

We study the complexity of heavy-tailed sampling and present a separation result in terms of obtaining high-accuracy versus low-accuracy guarantees i.e., samplers that require only $O(\log(1/\varepsilon))$ versus $\Omega(\text{poly}(1/\varepsilon))$ iterations to output a sample which is $\varepsilon$-close to the target in $\chi^2$-divergence. Our results are presented for proximal samplers that are based on Gaussian versus stable oracles. We show that proximal samplers based on the Gaussian oracle have a fundamental barrier in that they necessarily achieve only low-accuracy guarantees when sampling from a class of heavy-tailed targets. In contrast, proximal samplers based on the stable oracle exhibit high-accuracy guarantees, thereby overcoming the aforementioned limitation. We also prove lower bounds for samplers under the stable oracle and show that our upper bounds cannot be fundamentally improved.

Gradient-Based Feature Learning under Structured Data

Recent works have demonstrated that the sample complexity of gradient-based learning of single index models, i.e. functions that depend on a 1-dimensional projection of the input data, is governed by their information exponent. However, these results are only concerned with isotropic data, while in practice the input often contains additional structure which can implicitly guide the algorithm. In this work, we investigate the effect of a spiked covariance structure and reveal several interesting phenomena. First, we show that in the anisotropic setting, the commonly used spherical gradient dynamics may fail to recover the true direction, even when the spike is perfectly aligned with the target direction. Next, we show that appropriate weight normalization that is reminiscent of batch normalization can alleviate this issue. Further, by exploiting the alignment between the (spiked) input covariance and the target, we obtain improved sample complexity compared to the isotropic case. In particular, under the spiked model with a suitably large spike, the sample complexity of gradient-based training can be made independent of the information exponent while also outperforming lower bounds for rotationally invariant kernel methods.

Towards a Complete Analysis of Langevin Monte Carlo: Beyond Poincaré Inequality

Langevin diffusions are rapidly convergent under appropriate functional inequality assumptions. Hence, it is natural to expect that with additional smoothness conditions to handle the discretization errors, their discretizations like the Langevin Monte Carlo (LMC) converge in a similar fashion. This research program was initiated by Vemapala and Wibisono (2019), who established results under log-Sobolev inequalities. Chewi et al. (2022) extended the results to handle the case of Poincar\'e inequalities. In this paper, we go beyond Poincar\'e inequalities, and push this research program to its limit. We do so by establishing upper and lower bounds for Langevin diffusions and LMC under weak Poincar\'e inequalities that are satisfied by a large class of densities including polynomially-decaying heavy-tailed densities (i.e., Cauchy-type). Our results explicitly quantify the effect of the initializer on the performance of the LMC algorithm. In particular, we show that as the tail goes from sub-Gaussian, to sub-exponential, and finally to Cauchy-like, the dependency on the initial error goes from being logarithmic, to polynomial, and then finally to being exponential. This three-step phase transition is in particular unavoidable as demonstrated by our lower bounds, clearly defining the boundaries of LMC.

Neural Networks Efficiently Learn Low-Dimensional Representations with SGD

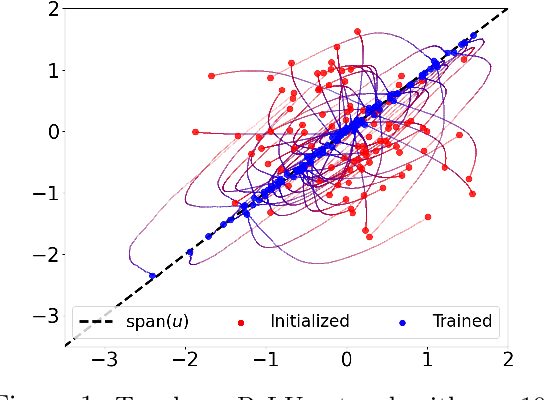
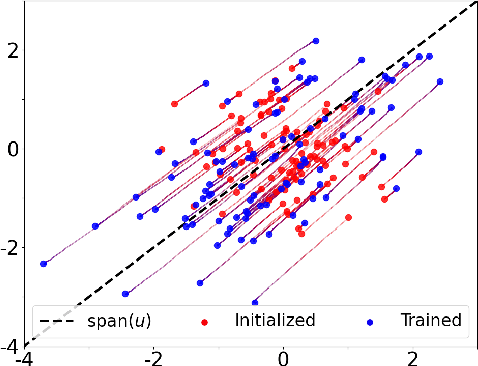
We study the problem of training a two-layer neural network (NN) of arbitrary width using stochastic gradient descent (SGD) where the input $\boldsymbol{x}\in \mathbb{R}^d$ is Gaussian and the target $y \in \mathbb{R}$ follows a multiple-index model, i.e., $y=g(\langle\boldsymbol{u_1},\boldsymbol{x}\rangle,...,\langle\boldsymbol{u_k},\boldsymbol{x}\rangle)$ with a noisy link function $g$. We prove that the first-layer weights of the NN converge to the $k$-dimensional principal subspace spanned by the vectors $\boldsymbol{u_1},...,\boldsymbol{u_k}$ of the true model, when online SGD with weight decay is used for training. This phenomenon has several important consequences when $k \ll d$. First, by employing uniform convergence on this smaller subspace, we establish a generalization error bound of $\mathcal{O}(\sqrt{{kd}/{T}})$ after $T$ iterations of SGD, which is independent of the width of the NN. We further demonstrate that, SGD-trained ReLU NNs can learn a single-index target of the form $y=f(\langle\boldsymbol{u},\boldsymbol{x}\rangle) + \epsilon$ by recovering the principal direction, with a sample complexity linear in $d$ (up to log factors), where $f$ is a monotonic function with at most polynomial growth, and $\epsilon$ is the noise. This is in contrast to the known $d^{\Omega(p)}$ sample requirement to learn any degree $p$ polynomial in the kernel regime, and it shows that NNs trained with SGD can outperform the neural tangent kernel at initialization. Finally, we also provide compressibility guarantees for NNs using the approximate low-rank structure produced by SGD.