On Fitting Flow Models with Large Sinkhorn Couplings

Flow models transform data gradually from one modality (e.g. noise) onto another (e.g. images). Such models are parameterized by a time-dependent velocity field, trained to fit segments connecting pairs of source and target points. When the pairing between source and target points is given, training flow models boils down to a supervised regression problem. When no such pairing exists, as is the case when generating data from noise, training flows is much harder. A popular approach lies in picking source and target points independently. This can, however, lead to velocity fields that are slow to train, but also costly to integrate at inference time. In theory, one would greatly benefit from training flow models by sampling pairs from an optimal transport (OT) measure coupling source and target, since this would lead to a highly efficient flow solving the Benamou and Brenier dynamical OT problem. In practice, recent works have proposed to sample mini-batches of $n$ source and $n$ target points and reorder them using an OT solver to form better pairs. These works have advocated using batches of size $n\approx 256$, and considered OT solvers that return couplings that are either sharp (using e.g. the Hungarian algorithm) or blurred (using e.g. entropic regularization, a.k.a. Sinkhorn). We follow in the footsteps of these works by exploring the benefits of increasing $n$ by three to four orders of magnitude, and look more carefully on the effect of the entropic regularization $\varepsilon$ used in the Sinkhorn algorithm. Our analysis is facilitated by new scale invariant quantities to report the sharpness of a coupling, while our sharded computations across multiple GPU or GPU nodes allow scaling up $n$. We show that in both synthetic and image generation tasks, flow models greatly benefit when fitted with large Sinkhorn couplings, with a low entropic regularization $\varepsilon$.

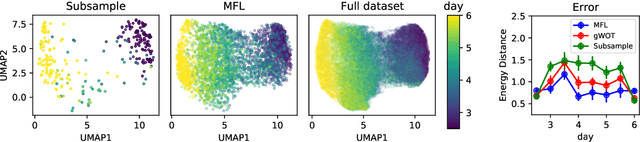
Inferring stochastic dynamics with growth from cross-sectional data

Time-resolved single-cell omics data offers high-throughput, genome-wide measurements of cellular states, which are instrumental to reverse-engineer the processes underpinning cell fate. Such technologies are inherently destructive, allowing only cross-sectional measurements of the underlying stochastic dynamical system. Furthermore, cells may divide or die in addition to changing their molecular state. Collectively these present a major challenge to inferring realistic biophysical models. We present a novel approach, \emph{unbalanced} probability flow inference, that addresses this challenge for biological processes modelled as stochastic dynamics with growth. By leveraging a Lagrangian formulation of the Fokker-Planck equation, our method accurately disentangles drift from intrinsic noise and growth. We showcase the applicability of our approach through evaluation on a range of simulated and real single-cell RNA-seq datasets. Comparing to several existing methods, we find our method achieves higher accuracy while enjoying a simple two-step training scheme.

Attention Sinks and Outlier Features: A 'Catch, Tag, and Release' Mechanism for Embeddings

Two prominent features of large language models (LLMs) is the presence of large-norm (outlier) features and the tendency for tokens to attend very strongly to a select few tokens. Despite often having no semantic relevance, these select tokens, called attention sinks, along with the large outlier features, have proven important for model performance, compression, and streaming. Consequently, investigating the roles of these phenomena within models and exploring how they might manifest in the model parameters has become an area of active interest. Through an empirical investigation, we demonstrate that attention sinks utilize outlier features to: catch a sequence of tokens, tag the captured tokens by applying a common perturbation, and then release the tokens back into the residual stream, where the tagged tokens are eventually retrieved. We prove that simple tasks, like averaging, necessitate the 'catch, tag, release' mechanism hence explaining why it would arise organically in modern LLMs. Our experiments also show that the creation of attention sinks can be completely captured in the model parameters using low-rank matrices, which has important implications for model compression and substantiates the success of recent approaches that incorporate a low-rank term to offset performance degradation.

Identifying Drift, Diffusion, and Causal Structure from Temporal Snapshots

Stochastic differential equations (SDEs) are a fundamental tool for modelling dynamic processes, including gene regulatory networks (GRNs), contaminant transport, financial markets, and image generation. However, learning the underlying SDE from observational data is a challenging task, especially when individual trajectories are not observable. Motivated by burgeoning research in single-cell datasets, we present the first comprehensive approach for jointly estimating the drift and diffusion of an SDE from its temporal marginals. Assuming linear drift and additive diffusion, we prove that these parameters are identifiable from marginals if and only if the initial distribution is not invariant to a class of generalized rotations, a condition that is satisfied by most distributions. We further prove that the causal graph of any SDE with additive diffusion can be recovered from the SDE parameters. To complement this theory, we adapt entropy-regularized optimal transport to handle anisotropic diffusion, and introduce APPEX (Alternating Projection Parameter Estimation from $X_0$), an iterative algorithm designed to estimate the drift, diffusion, and causal graph of an additive noise SDE, solely from temporal marginals. We show that each of these steps are asymptotically optimal with respect to the Kullback-Leibler divergence, and demonstrate APPEX's effectiveness on simulated data from linear additive noise SDEs.

Sparsest Models Elude Pruning: An Exposé of Pruning's Current Capabilities

Pruning has emerged as a promising approach for compressing large-scale models, yet its effectiveness in recovering the sparsest of models has not yet been explored. We conducted an extensive series of 485,838 experiments, applying a range of state-of-the-art pruning algorithms to a synthetic dataset we created, named the Cubist Spiral. Our findings reveal a significant gap in performance compared to ideal sparse networks, which we identified through a novel combinatorial search algorithm. We attribute this performance gap to current pruning algorithms' poor behaviour under overparameterization, their tendency to induce disconnected paths throughout the network, and their propensity to get stuck at suboptimal solutions, even when given the optimal width and initialization. This gap is concerning, given the simplicity of the network architectures and datasets used in our study. We hope that our research encourages further investigation into new pruning techniques that strive for true network sparsity.

Manifold Learning with Sparse Regularised Optimal Transport

Manifold learning is a central task in modern statistics and data science. Many datasets (cells, documents, images, molecules) can be represented as point clouds embedded in a high dimensional ambient space, however the degrees of freedom intrinsic to the data are usually far fewer than the number of ambient dimensions. The task of detecting a latent manifold along which the data are embedded is a prerequisite for a wide family of downstream analyses. Real-world datasets are subject to noisy observations and sampling, so that distilling information about the underlying manifold is a major challenge. We propose a method for manifold learning that utilises a symmetric version of optimal transport with a quadratic regularisation that constructs a sparse and adaptive affinity matrix, that can be interpreted as a generalisation of the bistochastic kernel normalisation. We prove that the resulting kernel is consistent with a Laplace-type operator in the continuous limit, establish robustness to heteroskedastic noise and exhibit these results in simulations. We identify a highly efficient computational scheme for computing this optimal transport for discrete data and demonstrate that it outperforms competing methods in a set of examples.

Quadratically Regularized Optimal Transport: nearly optimal potentials and convergence of discrete Laplace operators

We consider the conjecture proposed in Matsumoto, Zhang and Schiebinger (2022) suggesting that optimal transport with quadratic regularisation can be used to construct a graph whose discrete Laplace operator converges to the Laplace--Beltrami operator. We derive first order optimal potentials for the problem under consideration and find that the resulting solutions exhibit a surprising resemblance to the well-known Barenblatt--Prattle solution of the porous medium equation. Then, relying on these first order optimal potentials, we derive the pointwise $L^2$-limit of such discrete operators built from an i.i.d. random sample on a smooth compact manifold. Simulation results complementing the limiting distribution results are also presented.

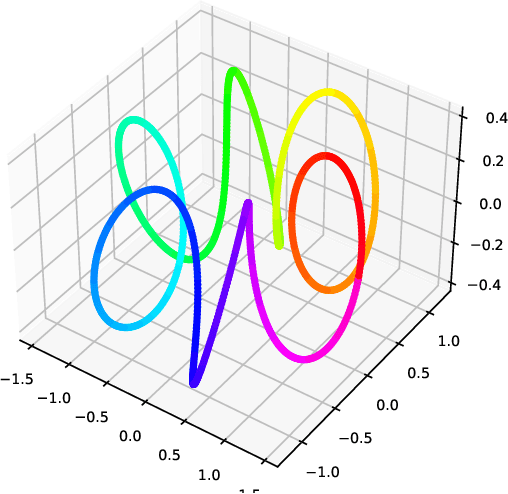
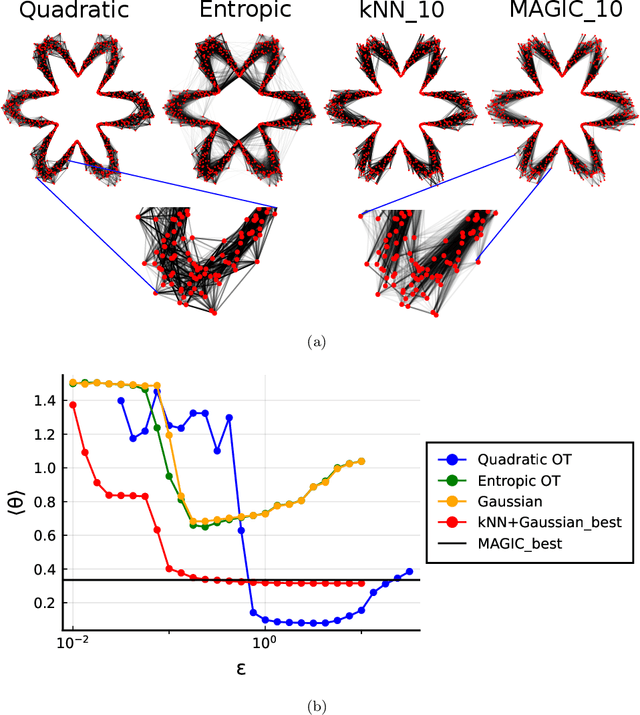
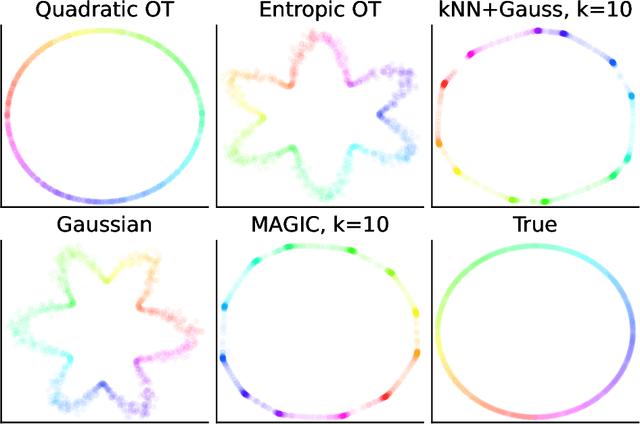
Beyond kNN: Adaptive, Sparse Neighborhood Graphs via Optimal Transport

Nearest neighbour graphs are widely used to capture the geometry or topology of a dataset. One of the most common strategies to construct such a graph is based on selecting a fixed number k of nearest neighbours (kNN) for each point. However, the kNN heuristic may become inappropriate when sampling density or noise level varies across datasets. Strategies that try to get around this typically introduce additional parameters that need to be tuned. We propose a simple approach to construct an adaptive neighbourhood graph from a single parameter, based on quadratically regularised optimal transport. Our numerical experiments show that graphs constructed in this manner perform favourably in unsupervised and semi-supervised learning applications.

Trajectory Inference via Mean-field Langevin in Path Space

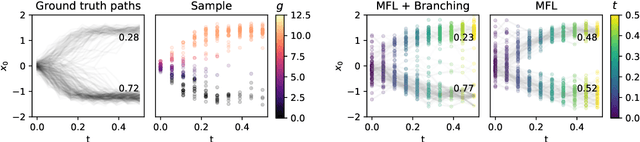
Trajectory inference aims at recovering the dynamics of a population from snapshots of its temporal marginals. To solve this task, a min-entropy estimator relative to the Wiener measure in path space was introduced by Lavenant et al. arXiv:2102.09204, and shown to consistently recover the dynamics of a large class of drift-diffusion processes from the solution of an infinite dimensional convex optimization problem. In this paper, we introduce a grid-free algorithm to compute this estimator. Our method consists in a family of point clouds (one per snapshot) coupled via Schr\"odinger bridges which evolve with noisy gradient descent. We study the mean-field limit of the dynamics and prove its global convergence at an exponential rate to the desired estimator. Overall, this leads to an inference method with end-to-end theoretical guarantees that solves an interpretable model for trajectory inference. We also present how to adapt the method to deal with mass variations, a useful extension when dealing with single cell RNA-sequencing data where cells can branch and die.

Towards a mathematical theory of trajectory inference

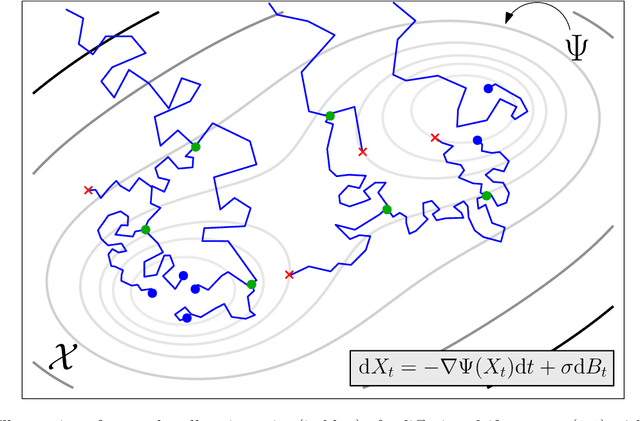
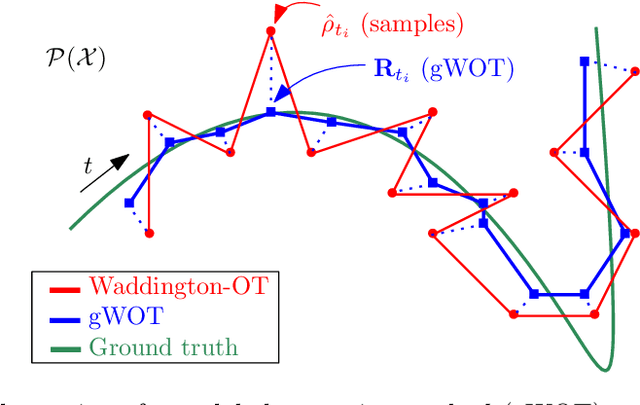
We devise a theoretical framework and a numerical method to infer trajectories of a stochastic process from snapshots of its temporal marginals. This problem arises in the analysis of single cell RNA-sequencing data, which provide high dimensional measurements of cell states but cannot track the trajectories of the cells over time. We prove that for a class of stochastic processes it is possible to recover the ground truth trajectories from limited samples of the temporal marginals at each time-point, and provide an efficient algorithm to do so in practice. The method we develop, Global Waddington-OT (gWOT), boils down to a smooth convex optimization problem posed globally over all time-points involving entropy-regularized optimal transport. We demonstrate that this problem can be solved efficiently in practice and yields good reconstructions, as we show on several synthetic and real datasets.