Langevin SDEs have unique transient dynamics

The overdamped Langevin stochastic differential equation (SDE) is a classical physical model used for chemical, genetic, and hydrological dynamics. In this work, we prove that the drift and diffusion terms of a Langevin SDE are jointly identifiable from temporal marginal distributions if and only if the process is observed out of equilibrium. This complete characterization of structural identifiability removes the long-standing assumption that the diffusion must be known to identify the drift. We then complement our theory with experiments in the finite sample setting and study the practical identifiability of the drift and diffusion, in order to propose heuristics for optimal data collection.

Identifying Drift, Diffusion, and Causal Structure from Temporal Snapshots

Stochastic differential equations (SDEs) are a fundamental tool for modelling dynamic processes, including gene regulatory networks (GRNs), contaminant transport, financial markets, and image generation. However, learning the underlying SDE from observational data is a challenging task, especially when individual trajectories are not observable. Motivated by burgeoning research in single-cell datasets, we present the first comprehensive approach for jointly estimating the drift and diffusion of an SDE from its temporal marginals. Assuming linear drift and additive diffusion, we prove that these parameters are identifiable from marginals if and only if the initial distribution is not invariant to a class of generalized rotations, a condition that is satisfied by most distributions. We further prove that the causal graph of any SDE with additive diffusion can be recovered from the SDE parameters. To complement this theory, we adapt entropy-regularized optimal transport to handle anisotropic diffusion, and introduce APPEX (Alternating Projection Parameter Estimation from $X_0$), an iterative algorithm designed to estimate the drift, diffusion, and causal graph of an additive noise SDE, solely from temporal marginals. We show that each of these steps are asymptotically optimal with respect to the Kullback-Leibler divergence, and demonstrate APPEX's effectiveness on simulated data from linear additive noise SDEs.

A Zero Auxiliary Knowledge Membership Inference Attack on Aggregate Location Data

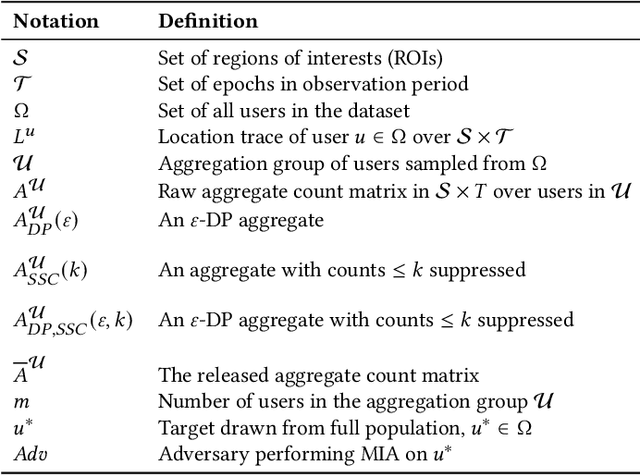
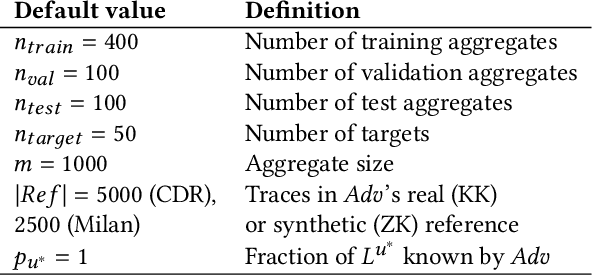
Location data is frequently collected from populations and shared in aggregate form to guide policy and decision making. However, the prevalence of aggregated data also raises the privacy concern of membership inference attacks (MIAs). MIAs infer whether an individual's data contributed to the aggregate release. Although effective MIAs have been developed for aggregate location data, these require access to an extensive auxiliary dataset of individual traces over the same locations, which are collected from a similar population. This assumption is often impractical given common privacy practices surrounding location data. To measure the risk of an MIA performed by a realistic adversary, we develop the first Zero Auxiliary Knowledge (ZK) MIA on aggregate location data, which eliminates the need for an auxiliary dataset of real individual traces. Instead, we develop a novel synthetic approach, such that suitable synthetic traces are generated from the released aggregate. We also develop methods to correct for bias and noise, to show that our synthetic-based attack is still applicable when privacy mechanisms are applied prior to release. Using two large-scale location datasets, we demonstrate that our ZK MIA matches the state-of-the-art Knock-Knock (KK) MIA across a wide range of settings, including popular implementations of differential privacy (DP) and suppression of small counts. Furthermore, we show that ZK MIA remains highly effective even when the adversary only knows a small fraction (10%) of their target's location history. This demonstrates that effective MIAs can be performed by realistic adversaries, highlighting the need for strong DP protection.

Ultra Marginal Feature Importance

Scientists frequently prioritize learning from data rather than training the best possible model; however, research in machine learning often prioritizes the latter. The development of marginal feature importance methods, such as marginal contribution feature importance, attempts to break this trend by providing a useful framework for explaining relationships in data in an interpretable fashion. In this work, we generalize the framework of marginal contribution feature importance to improve performance with regards to detecting correlated interactions and reducing runtime. To do so, we consider "information subsets" of the set of features $F$ and show that our importance metric can be computed directly after applying fair representation learning methods from the AI fairness literature. The methods of optimal transport and linear regression are considered and explored experimentally for removing all the information of our feature of interest $f$ from the feature set $F$. Given these implementations, we show on real and simulated data that ultra marginal feature importance performs at least as well as marginal contribution feature importance, with substantially faster computation time and better performance in the presence of correlated interactions and unrelated features.