Langevin SDEs have unique transient dynamics

The overdamped Langevin stochastic differential equation (SDE) is a classical physical model used for chemical, genetic, and hydrological dynamics. In this work, we prove that the drift and diffusion terms of a Langevin SDE are jointly identifiable from temporal marginal distributions if and only if the process is observed out of equilibrium. This complete characterization of structural identifiability removes the long-standing assumption that the diffusion must be known to identify the drift. We then complement our theory with experiments in the finite sample setting and study the practical identifiability of the drift and diffusion, in order to propose heuristics for optimal data collection.

Identifying Drift, Diffusion, and Causal Structure from Temporal Snapshots

Stochastic differential equations (SDEs) are a fundamental tool for modelling dynamic processes, including gene regulatory networks (GRNs), contaminant transport, financial markets, and image generation. However, learning the underlying SDE from observational data is a challenging task, especially when individual trajectories are not observable. Motivated by burgeoning research in single-cell datasets, we present the first comprehensive approach for jointly estimating the drift and diffusion of an SDE from its temporal marginals. Assuming linear drift and additive diffusion, we prove that these parameters are identifiable from marginals if and only if the initial distribution is not invariant to a class of generalized rotations, a condition that is satisfied by most distributions. We further prove that the causal graph of any SDE with additive diffusion can be recovered from the SDE parameters. To complement this theory, we adapt entropy-regularized optimal transport to handle anisotropic diffusion, and introduce APPEX (Alternating Projection Parameter Estimation from $X_0$), an iterative algorithm designed to estimate the drift, diffusion, and causal graph of an additive noise SDE, solely from temporal marginals. We show that each of these steps are asymptotically optimal with respect to the Kullback-Leibler divergence, and demonstrate APPEX's effectiveness on simulated data from linear additive noise SDEs.

A critical appraisal of water table depth estimation: Challenges and opportunities within machine learning

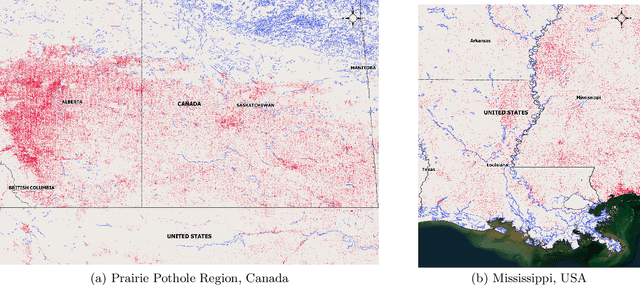
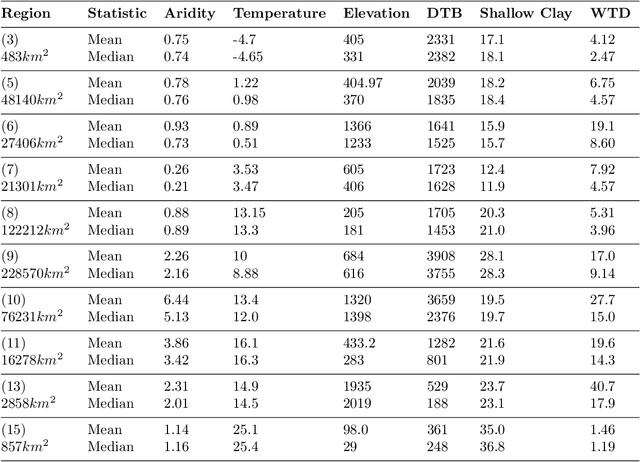
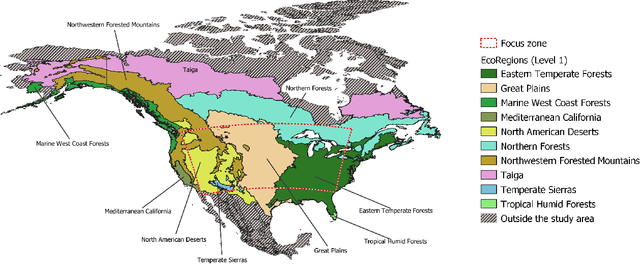
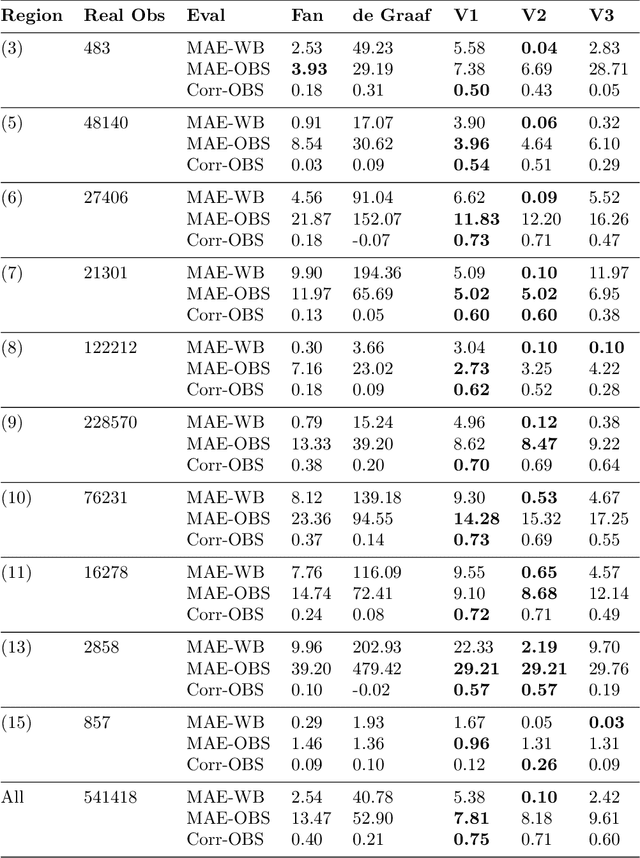
Fine-resolution spatial patterns of water table depth (WTD) can inform the dynamics of groundwater-dependent systems, including ecological, hydrological, and anthropogenic systems. Generally, a large-scale (e.g., continental or global) spatial map of static WTD can be simulated using either physically-based (PB) or machine learning-based (ML) models. We construct three fine-resolution (500 m) ML simulations of WTD, using the XGBoost algorithm and more than 20 million real and proxy observations of WTD, across the United States and Canada. The three ML models were constrained using known physical relations between WTD's drivers and WTD and were trained by sequentially adding real and proxy observations of WTD. We interpret the black box of our physically constrained ML models and compare it against available literature in groundwater hydrology. Through an extensive (pixel-by-pixel) evaluation, we demonstrate that our models can more accurately predict unseen real and proxy observations of WTD across most of North America's ecoregions compared to three available PB simulations of WTD. However, we still argue that large-scale WTD estimation is far from being a solved problem. We reason that due to biased and untrustworthy observational data, the misspecification of physically-based equations, and the over-flexibility of machine learning models, our community's confidence in ML or PB simulations of WTD is far too high and verifiably accurate simulations of WTD do not yet exist in the literature, particularly in arid high-elevation landscapes. Ultimately, we thoroughly discuss future directions that may help hydrogeologists decide how to proceed with WTD estimations, with a particular focus on the application of machine learning.

Ultra Marginal Feature Importance

Scientists frequently prioritize learning from data rather than training the best possible model; however, research in machine learning often prioritizes the latter. The development of marginal feature importance methods, such as marginal contribution feature importance, attempts to break this trend by providing a useful framework for explaining relationships in data in an interpretable fashion. In this work, we generalize the framework of marginal contribution feature importance to improve performance with regards to detecting correlated interactions and reducing runtime. To do so, we consider "information subsets" of the set of features $F$ and show that our importance metric can be computed directly after applying fair representation learning methods from the AI fairness literature. The methods of optimal transport and linear regression are considered and explored experimentally for removing all the information of our feature of interest $f$ from the feature set $F$. Given these implementations, we show on real and simulated data that ultra marginal feature importance performs at least as well as marginal contribution feature importance, with substantially faster computation time and better performance in the presence of correlated interactions and unrelated features.