Identifying Drift, Diffusion, and Causal Structure from Temporal Snapshots

Stochastic differential equations (SDEs) are a fundamental tool for modelling dynamic processes, including gene regulatory networks (GRNs), contaminant transport, financial markets, and image generation. However, learning the underlying SDE from observational data is a challenging task, especially when individual trajectories are not observable. Motivated by burgeoning research in single-cell datasets, we present the first comprehensive approach for jointly estimating the drift and diffusion of an SDE from its temporal marginals. Assuming linear drift and additive diffusion, we prove that these parameters are identifiable from marginals if and only if the initial distribution is not invariant to a class of generalized rotations, a condition that is satisfied by most distributions. We further prove that the causal graph of any SDE with additive diffusion can be recovered from the SDE parameters. To complement this theory, we adapt entropy-regularized optimal transport to handle anisotropic diffusion, and introduce APPEX (Alternating Projection Parameter Estimation from $X_0$), an iterative algorithm designed to estimate the drift, diffusion, and causal graph of an additive noise SDE, solely from temporal marginals. We show that each of these steps are asymptotically optimal with respect to the Kullback-Leibler divergence, and demonstrate APPEX's effectiveness on simulated data from linear additive noise SDEs.

Log-concave density estimation in undirected graphical models

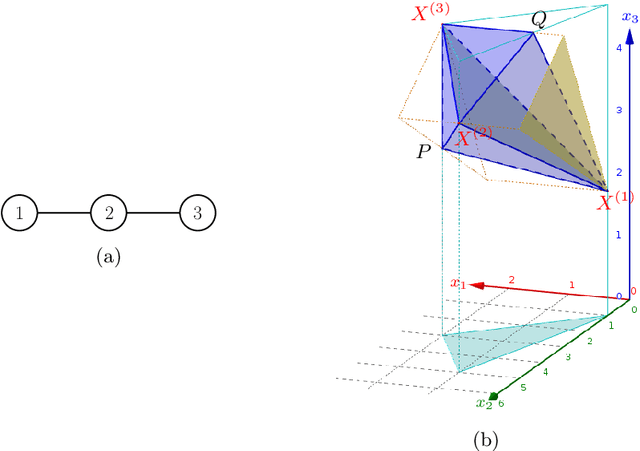
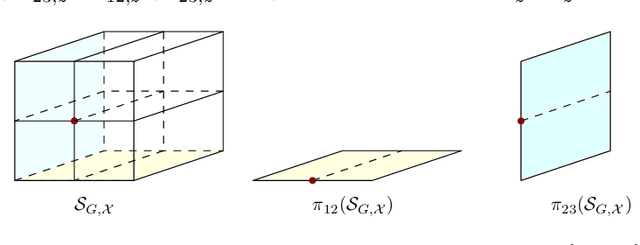
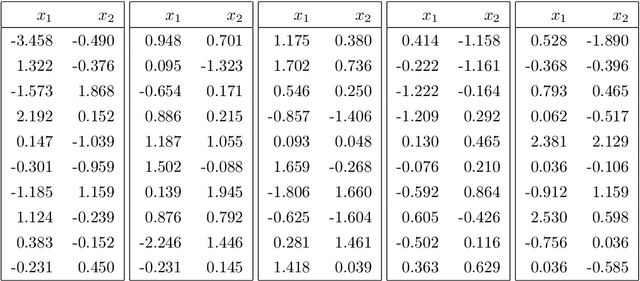
We study the problem of maximum likelihood estimation of densities that are log-concave and lie in the graphical model corresponding to a given undirected graph $G$. We show that the maximum likelihood estimate (MLE) is the product of the exponentials of several tent functions, one for each maximal clique of $G$. While the set of log-concave densities in a graphical model is infinite-dimensional, our results imply that the MLE can be found by solving a finite-dimensional convex optimization problem. We provide an implementation and a few examples. Furthermore, we show that the MLE exists and is unique with probability 1 as long as the number of sample points is larger than the size of the largest clique of $G$ when $G$ is chordal. We show that the MLE is consistent when the graph $G$ is a disjoint union of cliques. Finally, we discuss the conditions under which a log-concave density in the graphical model of $G$ has a log-concave factorization according to $G$.

Learning Linear Non-Gaussian Graphical Models with Multidirected Edges

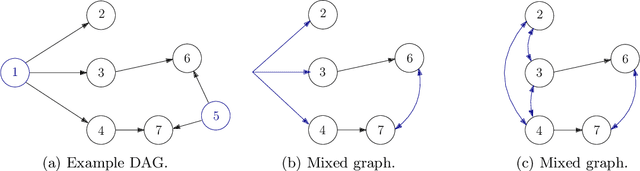
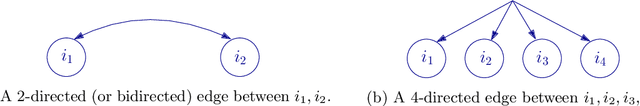
In this paper we propose a new method to learn the underlying acyclic mixed graph of a linear non-Gaussian structural equation model given observational data. We build on an algorithm proposed by Wang and Drton, and we show that one can augment the hidden variable structure of the recovered model by learning {\em multidirected edges} rather than only directed and bidirected ones. Multidirected edges appear when more than two of the observed variables have a hidden common cause. We detect the presence of such hidden causes by looking at higher order cumulants and exploiting the multi-trek rule. Our method recovers the correct structure when the underlying graph is a bow-free acyclic mixed graph with potential multi-directed edges.

Estimation of Monge Matrices

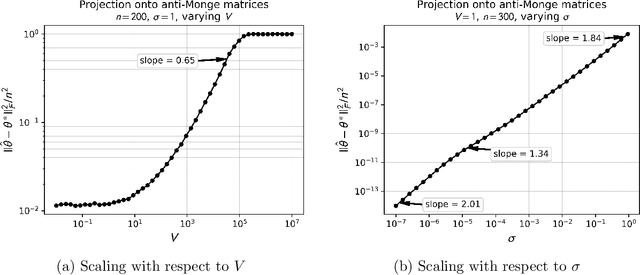
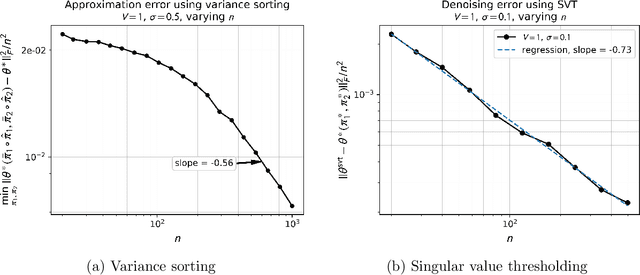
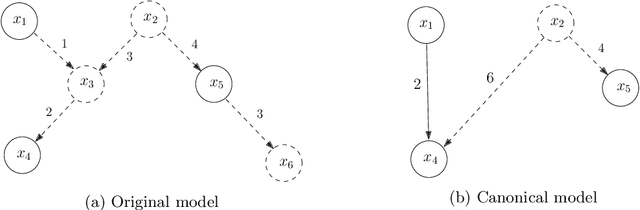
Monge matrices and their permuted versions known as pre-Monge matrices naturally appear in many domains across science and engineering. While the rich structural properties of such matrices have long been leveraged for algorithmic purposes, little is known about their impact on statistical estimation. In this work, we propose to view this structure as a shape constraint and study the problem of estimating a Monge matrix subject to additive random noise. More specifically, we establish the minimax rates of estimation of Monge and pre-Monge matrices. In the case of pre-Monge matrices, the minimax-optimal least-squares estimator is not efficiently computable, and we propose two efficient estimators and establish their rates of convergence. Our theoretical findings are supported by numerical experiments.

Duality of Graphical Models and Tensor Networks

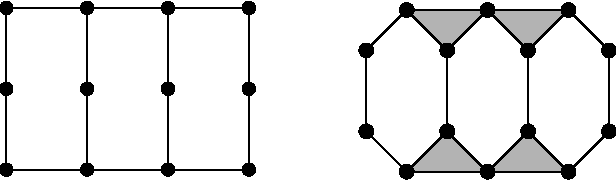
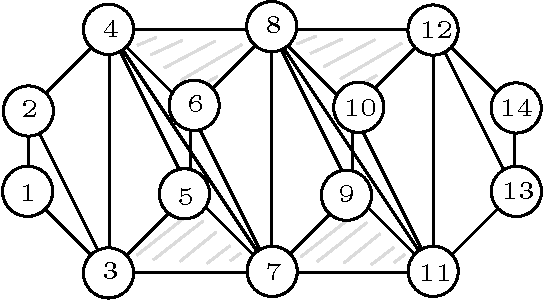
In this article we show the duality between tensor networks and undirected graphical models with discrete variables. We study tensor networks on hypergraphs, which we call tensor hypernetworks. We show that the tensor hypernetwork on a hypergraph exactly corresponds to the graphical model given by the dual hypergraph. We translate various notions under duality. For example, marginalization in a graphical model is dual to contraction in the tensor network. Algorithms also translate under duality. We show that belief propagation corresponds to a known algorithm for tensor network contraction. This article is a reminder that the research areas of graphical models and tensor networks can benefit from interaction.