ABatRe-Sim: A Comprehensive Framework for Automated Battery Recycling Simulation

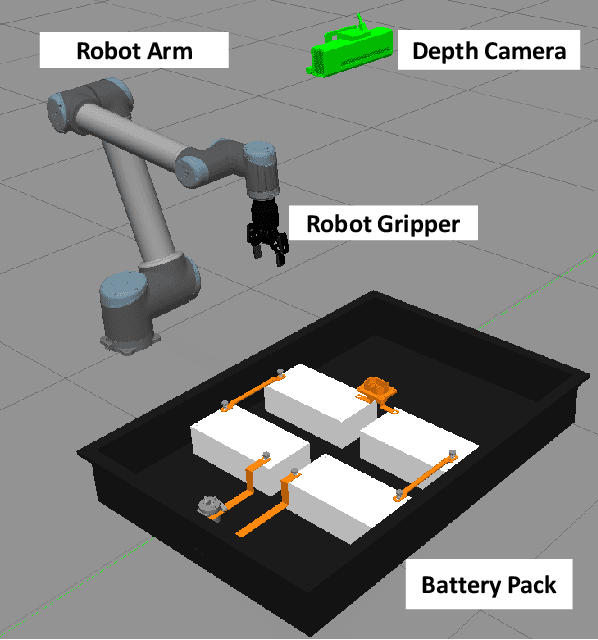
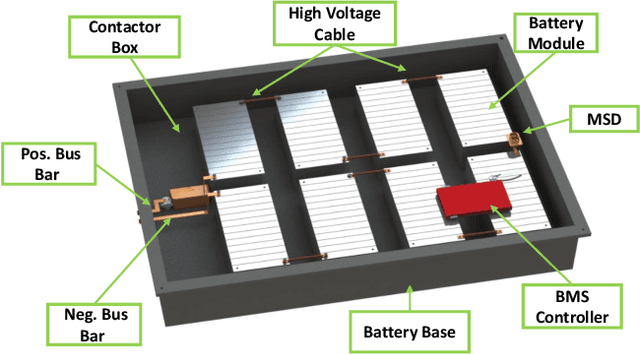
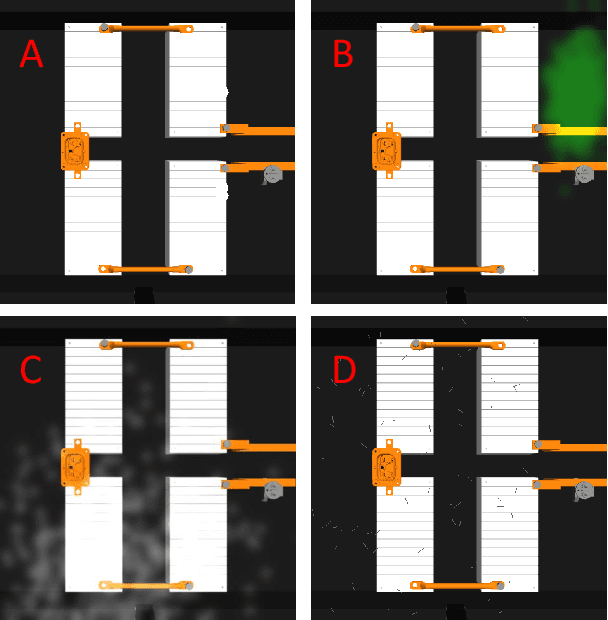
With the rapid surge in the number of on-road Electric Vehicles (EVs), the amount of spent lithium-ion (Li-ion) batteries is also expected to explosively grow. The spent battery packs contain valuable metal and materials that should be recovered, recycled, and reused. However, only less than 5% of the Li-ion batteries are currently recycled, due to a multitude of challenges in technology, logistics and regulation. Existing battery recycling is performed manually, which can pose a series of risks to the human operator as a consequence of remaining high voltage and chemical hazards. Therefore, there is a critical need to develop an automated battery recycling system. In this paper, we present ABatRe-sim, an open-source robotic battery recycling simulator, to facilitate the research and development in efficient and effective battery recycling au-omation. Specifically, we develop a detailed CAD model of the battery pack (with screws, wires, and battery modules), which is imported into Gazebo to enable robot-object interaction in the robot operating system (ROS) environment. It also allows the simulation of battery packs of various aging conditions. Furthermore, perception, planning, and control algorithms are developed to establish the benchmark to demonstrate the interface and realize the basic functionalities for further user customization. Discussions on the utilization and future extensions of the simulator are also presented.

Learning Linear Non-Gaussian Graphical Models with Multidirected Edges

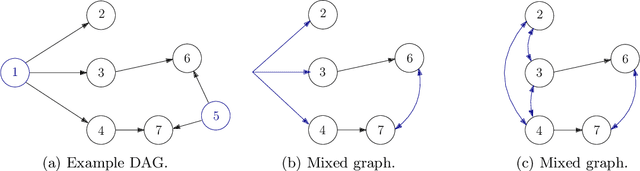
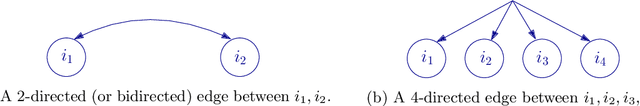
In this paper we propose a new method to learn the underlying acyclic mixed graph of a linear non-Gaussian structural equation model given observational data. We build on an algorithm proposed by Wang and Drton, and we show that one can augment the hidden variable structure of the recovered model by learning {\em multidirected edges} rather than only directed and bidirected ones. Multidirected edges appear when more than two of the observed variables have a hidden common cause. We detect the presence of such hidden causes by looking at higher order cumulants and exploiting the multi-trek rule. Our method recovers the correct structure when the underlying graph is a bow-free acyclic mixed graph with potential multi-directed edges.