Learning Linear Non-Gaussian Graphical Models with Multidirected Edges
Paper and Code
Oct 11, 2020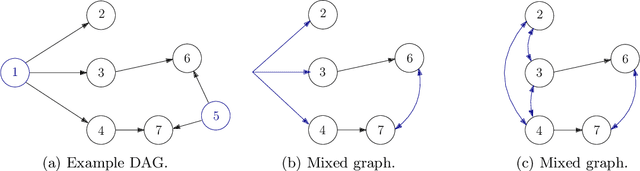
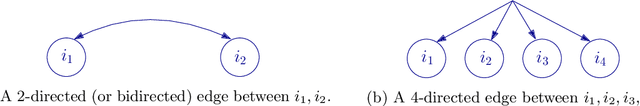

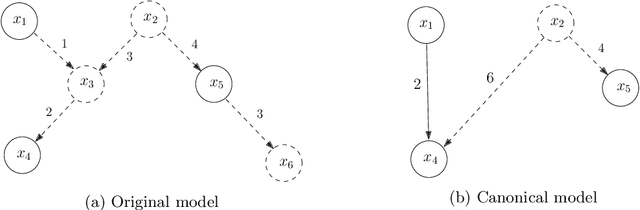
In this paper we propose a new method to learn the underlying acyclic mixed graph of a linear non-Gaussian structural equation model given observational data. We build on an algorithm proposed by Wang and Drton, and we show that one can augment the hidden variable structure of the recovered model by learning {\em multidirected edges} rather than only directed and bidirected ones. Multidirected edges appear when more than two of the observed variables have a hidden common cause. We detect the presence of such hidden causes by looking at higher order cumulants and exploiting the multi-trek rule. Our method recovers the correct structure when the underlying graph is a bow-free acyclic mixed graph with potential multi-directed edges.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge