NODAGS-Flow: Nonlinear Cyclic Causal Structure Learning

Learning causal relationships between variables is a well-studied problem in statistics, with many important applications in science. However, modeling real-world systems remain challenging, as most existing algorithms assume that the underlying causal graph is acyclic. While this is a convenient framework for developing theoretical developments about causal reasoning and inference, the underlying modeling assumption is likely to be violated in real systems, because feedback loops are common (e.g., in biological systems). Although a few methods search for cyclic causal models, they usually rely on some form of linearity, which is also limiting, or lack a clear underlying probabilistic model. In this work, we propose a novel framework for learning nonlinear cyclic causal graphical models from interventional data, called NODAGS-Flow. We perform inference via direct likelihood optimization, employing techniques from residual normalizing flows for likelihood estimation. Through synthetic experiments and an application to single-cell high-content perturbation screening data, we show significant performance improvements with our approach compared to state-of-the-art methods with respect to structure recovery and predictive performance.

Large-Scale Differentiable Causal Discovery of Factor Graphs

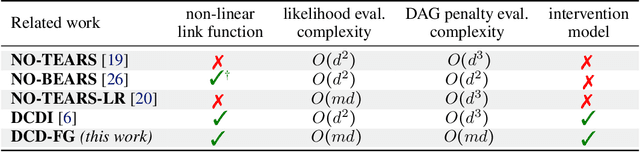
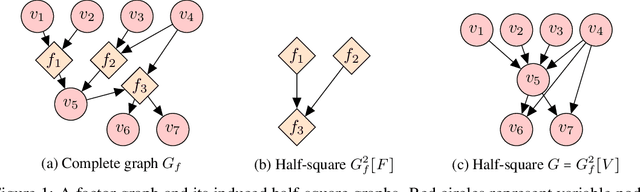
A common theme in causal inference is learning causal relationships between observed variables, also known as causal discovery. This is usually a daunting task, given the large number of candidate causal graphs and the combinatorial nature of the search space. Perhaps for this reason, most research has so far focused on relatively small causal graphs, with up to hundreds of nodes. However, recent advances in fields like biology enable generating experimental data sets with thousands of interventions followed by rich profiling of thousands of variables, raising the opportunity and urgent need for large causal graph models. Here, we introduce the notion of factor directed acyclic graphs (f-DAGs) as a way to restrict the search space to non-linear low-rank causal interaction models. Combining this novel structural assumption with recent advances that bridge the gap between causal discovery and continuous optimization, we achieve causal discovery on thousands of variables. Additionally, as a model for the impact of statistical noise on this estimation procedure, we study a model of edge perturbations of the f-DAG skeleton based on random graphs and quantify the effect of such perturbations on the f-DAG rank. This theoretical analysis suggests that the set of candidate f-DAGs is much smaller than the whole DAG space and thus more statistically robust in the high-dimensional regime where the underlying skeleton is hard to assess. We propose Differentiable Causal Discovery of Factor Graphs (DCD-FG), a scalable implementation of f-DAG constrained causal discovery for high-dimensional interventional data. DCD-FG uses a Gaussian non-linear low-rank structural equation model and shows significant improvements compared to state-of-the-art methods in both simulations as well as a recent large-scale single-cell RNA sequencing data set with hundreds of genetic interventions.

Estimation of Monge Matrices

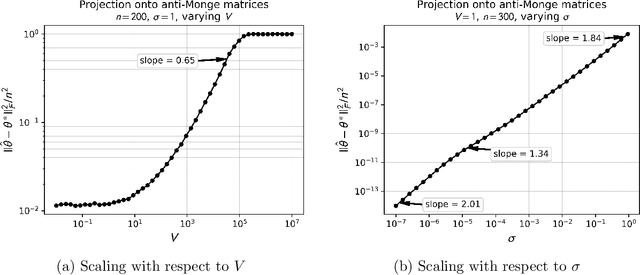
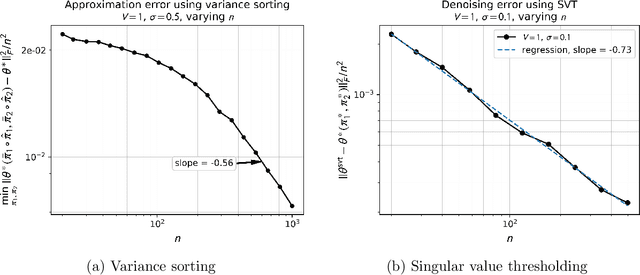
Monge matrices and their permuted versions known as pre-Monge matrices naturally appear in many domains across science and engineering. While the rich structural properties of such matrices have long been leveraged for algorithmic purposes, little is known about their impact on statistical estimation. In this work, we propose to view this structure as a shape constraint and study the problem of estimating a Monge matrix subject to additive random noise. More specifically, we establish the minimax rates of estimation of Monge and pre-Monge matrices. In the case of pre-Monge matrices, the minimax-optimal least-squares estimator is not efficiently computable, and we propose two efficient estimators and establish their rates of convergence. Our theoretical findings are supported by numerical experiments.

Statistical Optimal Transport via Factored Couplings

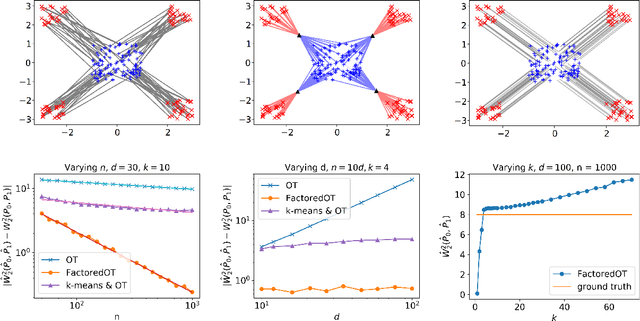
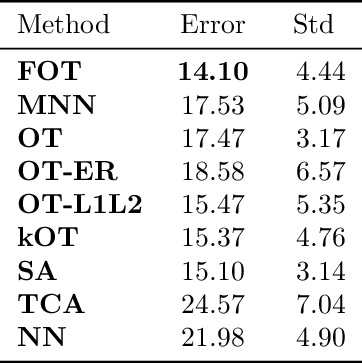
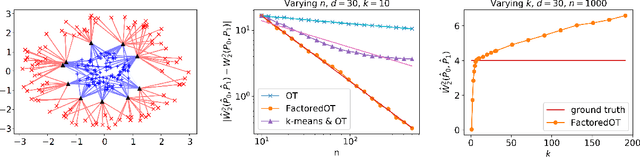
We propose a new method to estimate Wasserstein distances and optimal transport plans between two probability distributions from samples in high dimension. Unlike plug-in rules that simply replace the true distributions by their empirical counterparts, our method pro- motes couplings with low transport rank, a new structural assumption that is similar to the nonnegative rank of a matrix. Regularizing based on this assumption leads to drastic improvements on high-dimensional data for various tasks, including domain adaptation in single-cell RNA sequencing data. These findings are supported by a theoretical analysis that indicates that the transport rank is key in overcoming the curse of dimensionality inherent to data-driven optimal transport.