TRENDy: Temporal Regression of Effective Non-linear Dynamics

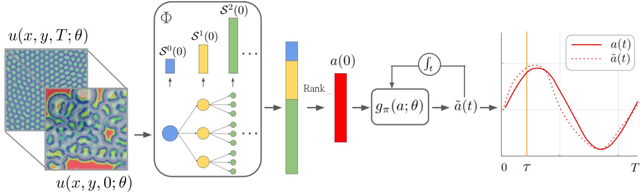
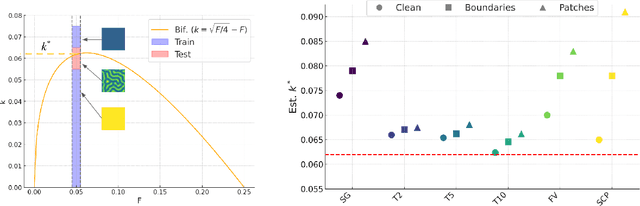
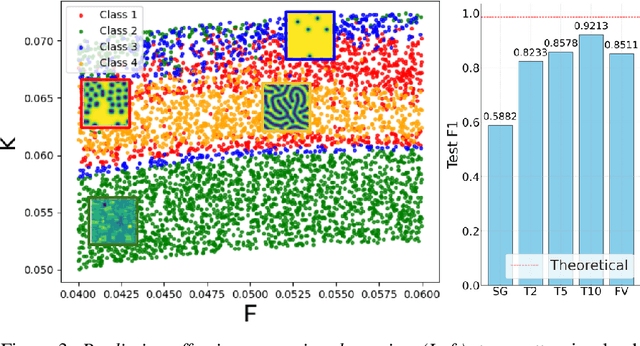
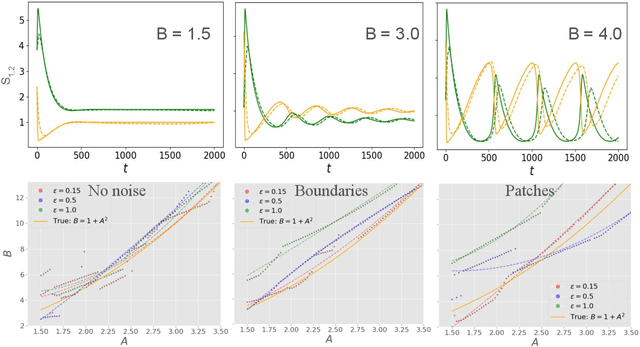
Spatiotemporal dynamics pervade the natural sciences, from the morphogen dynamics underlying patterning in animal pigmentation to the protein waves controlling cell division. A central challenge lies in understanding how controllable parameters induce qualitative changes in system behavior called bifurcations. This endeavor is made particularly difficult in realistic settings where governing partial differential equations (PDEs) are unknown and data is limited and noisy. To address this challenge, we propose TRENDy (Temporal Regression of Effective Nonlinear Dynamics), an equation-free approach to learning low-dimensional, predictive models of spatiotemporal dynamics. Following classical work in spatial coarse-graining, TRENDy first maps input data to a low-dimensional space of effective dynamics via a cascade of multiscale filtering operations. Our key insight is the recognition that these effective dynamics can be fit by a neural ordinary differential equation (NODE) having the same parameter space as the input PDE. The preceding filtering operations strongly regularize the phase space of the NODE, making TRENDy significantly more robust to noise compared to existing methods. We train TRENDy to predict the effective dynamics of synthetic and real data representing dynamics from across the physical and life sciences. We then demonstrate how our framework can automatically locate both Turing and Hopf bifurcations in unseen regions of parameter space. We finally apply our method to the analysis of spatial patterning of the ocellated lizard through development. We found that TRENDy's effective state not only accurately predicts spatial changes over time but also identifies distinct pattern features unique to different anatomical regions, highlighting the potential influence of surface geometry on reaction-diffusion mechanisms and their role in driving spatially varying pattern dynamics.

Let's do the time-warp-attend: Learning topological invariants of dynamical systems

Dynamical systems across the sciences, from electrical circuits to ecological networks, undergo qualitative and often catastrophic changes in behavior, called bifurcations, when their underlying parameters cross a threshold. Existing methods predict oncoming catastrophes in individual systems but are primarily time-series-based and struggle both to categorize qualitative dynamical regimes across diverse systems and to generalize to real data. To address this challenge, we propose a data-driven, physically-informed deep-learning framework for classifying dynamical regimes and characterizing bifurcation boundaries based on the extraction of topologically invariant features. We focus on the paradigmatic case of the supercritical Hopf bifurcation, which is used to model periodic dynamics across a wide range of applications. Our convolutional attention method is trained with data augmentations that encourage the learning of topological invariants which can be used to detect bifurcation boundaries in unseen systems and to design models of biological systems like oscillatory gene regulatory networks. We further demonstrate our method's use in analyzing real data by recovering distinct proliferation and differentiation dynamics along pancreatic endocrinogenesis trajectory in gene expression space based on single-cell data. Our method provides valuable insights into the qualitative, long-term behavior of a wide range of dynamical systems, and can detect bifurcations or catastrophic transitions in large-scale physical and biological systems.

Phase2vec: Dynamical systems embedding with a physics-informed convolutional network

Dynamical systems are found in innumerable forms across the physical and biological sciences, yet all these systems fall naturally into universal equivalence classes: conservative or dissipative, stable or unstable, compressible or incompressible. Predicting these classes from data remains an essential open challenge in computational physics at which existing time-series classification methods struggle. Here, we propose, \texttt{phase2vec}, an embedding method that learns high-quality, physically-meaningful representations of 2D dynamical systems without supervision. Our embeddings are produced by a convolutional backbone that extracts geometric features from flow data and minimizes a physically-informed vector field reconstruction loss. In an auxiliary training period, embeddings are optimized so that they robustly encode the equations of unseen data over and above the performance of a per-equation fitting method. The trained architecture can not only predict the equations of unseen data, but also, crucially, learns embeddings that respect the underlying semantics of the embedded physical systems. We validate the quality of learned embeddings investigating the extent to which physical categories of input data can be decoded from embeddings compared to standard blackbox classifiers and state-of-the-art time series classification techniques. We find that our embeddings encode important physical properties of the underlying data, including the stability of fixed points, conservation of energy, and the incompressibility of flows, with greater fidelity than competing methods. We finally apply our embeddings to the analysis of meteorological data, showing we can detect climatically meaningful features. Collectively, our results demonstrate the viability of embedding approaches for the discovery of dynamical features in physical systems.

Statistical Optimal Transport via Factored Couplings

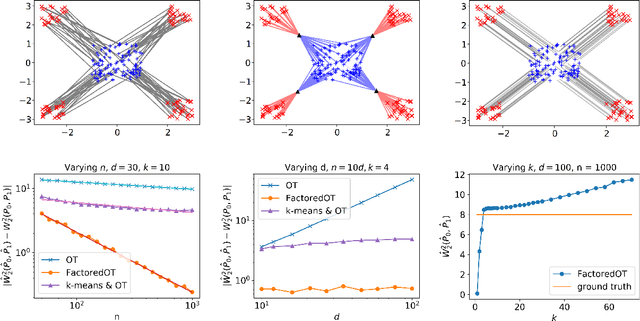
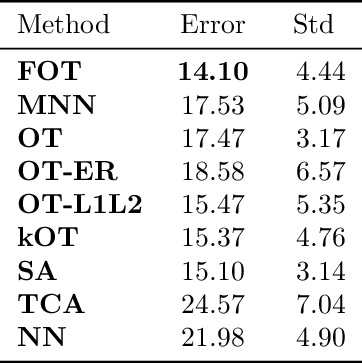
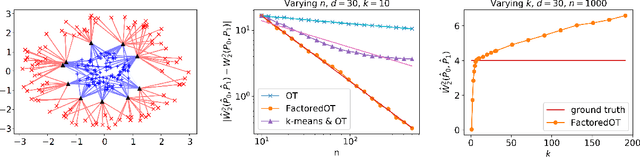
We propose a new method to estimate Wasserstein distances and optimal transport plans between two probability distributions from samples in high dimension. Unlike plug-in rules that simply replace the true distributions by their empirical counterparts, our method pro- motes couplings with low transport rank, a new structural assumption that is similar to the nonnegative rank of a matrix. Regularizing based on this assumption leads to drastic improvements on high-dimensional data for various tasks, including domain adaptation in single-cell RNA sequencing data. These findings are supported by a theoretical analysis that indicates that the transport rank is key in overcoming the curse of dimensionality inherent to data-driven optimal transport.