Statistical bounds for entropic optimal transport: sample complexity and the central limit theorem

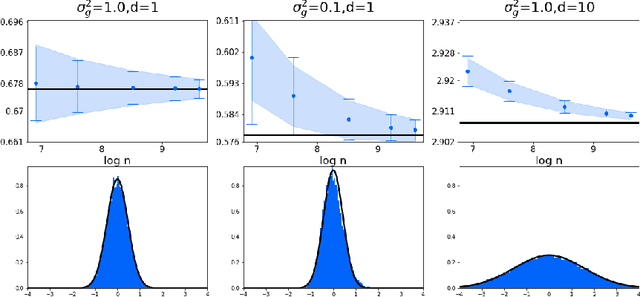
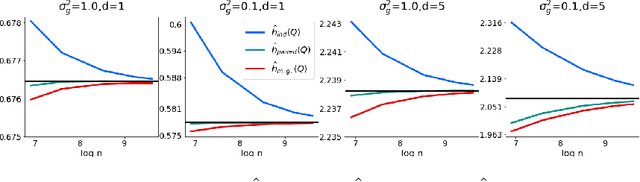
We prove several fundamental statistical bounds for entropic OT with the squared Euclidean cost between subgaussian probability measures in arbitrary dimension. First, through a new sample complexity result we establish the rate of convergence of entropic OT for empirical measures. Our analysis improves exponentially on the bound of Genevay et al. (2019) and extends their work to unbounded measures. Second, we establish a central limit theorem for entropic OT, based on techniques developed by Del Barrio and Loubes (2019). Previously, such a result was only known for finite metric spaces. As an application of our results, we develop and analyze a new technique for estimating the entropy of a random variable corrupted by gaussian noise.

Massively scalable Sinkhorn distances via the Nyström method

The Sinkhorn distance, a variant of the Wasserstein distance with entropic regularization, is an increasingly popular tool in machine learning and statistical inference. We give a simple, practical, parallelizable algorithm NYS-SINK, based on Nystr\"om approximation, for computing Sinkhorn distances on a massive scale. As we show in numerical experiments, our algorithm easily computes Sinkhorn distances on data sets hundreds of times larger than can be handled by state-of-the-art approaches. We also give provable guarantees establishing that the running time and memory requirements of our algorithm adapt to the intrinsic dimension of the underlying data.

Statistical Optimal Transport via Factored Couplings

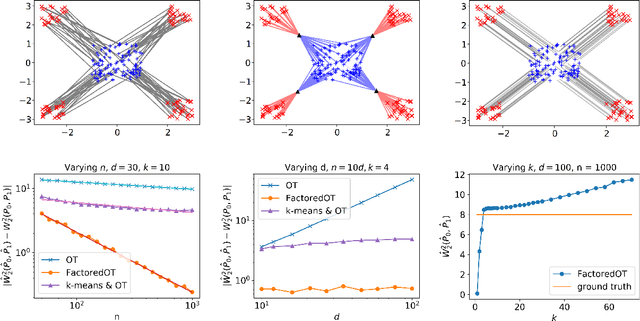
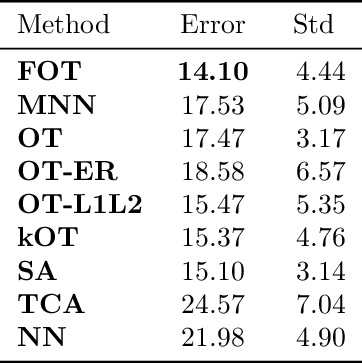
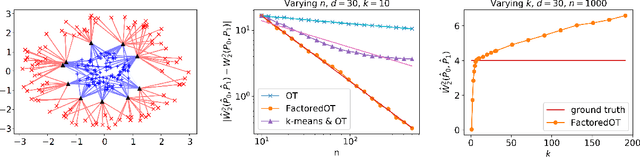
We propose a new method to estimate Wasserstein distances and optimal transport plans between two probability distributions from samples in high dimension. Unlike plug-in rules that simply replace the true distributions by their empirical counterparts, our method pro- motes couplings with low transport rank, a new structural assumption that is similar to the nonnegative rank of a matrix. Regularizing based on this assumption leads to drastic improvements on high-dimensional data for various tasks, including domain adaptation in single-cell RNA sequencing data. These findings are supported by a theoretical analysis that indicates that the transport rank is key in overcoming the curse of dimensionality inherent to data-driven optimal transport.

Uncoupled isotonic regression via minimum Wasserstein deconvolution

Isotonic regression is a standard problem in shape-constrained estimation where the goal is to estimate an unknown nondecreasing regression function $f$ from independent pairs $(x_i, y_i)$ where $\mathbb{E}[y_i]=f(x_i), i=1, \ldots n$. While this problem is well understood both statistically and computationally, much less is known about its uncoupled counterpart where one is given only the unordered sets $\{x_1, \ldots, x_n\}$ and $\{y_1, \ldots, y_n\}$. In this work, we leverage tools from optimal transport theory to derive minimax rates under weak moments conditions on $y_i$ and to give an efficient algorithm achieving optimal rates. Both upper and lower bounds employ moment-matching arguments that are also pertinent to learning mixtures of distributions and deconvolution.

An explicit analysis of the entropic penalty in linear programming

Solving linear programs by using entropic penalization has recently attracted new interest in the optimization community, since this strategy forms the basis for the fastest-known algorithms for the optimal transport problem, with many applications in modern large-scale machine learning. Crucial to these applications has been an analysis of how quickly solutions to the penalized program approach true optima to the original linear program. More than 20 years ago, Cominetti and San Mart\'in showed that this convergence is exponentially fast; however, their proof is asymptotic and does not give any indication of how accurately the entropic program approximates the original program for any particular choice of the penalization parameter. We close this long-standing gap in the literature regarding entropic penalization by giving a new proof of the exponential convergence, valid for any linear program. Our proof is non-asymptotic, yields explicit constants, and has the virtue of being extremely simple. We provide matching lower bounds and show that the entropic approach does not lead to a near-linear time approximation scheme for the linear assignment problem.

Near-linear time approximation algorithms for optimal transport via Sinkhorn iteration

Computing optimal transport distances such as the earth mover's distance is a fundamental problem in machine learning, statistics, and computer vision. Despite the recent introduction of several algorithms with good empirical performance, it is unknown whether general optimal transport distances can be approximated in near-linear time. This paper demonstrates that this ambitious goal is in fact achieved by Cuturi's Sinkhorn Distances. This result relies on a new analysis of Sinkhorn iteration, which also directly suggests a new greedy coordinate descent algorithm, Greenkhorn, with the same theoretical guarantees. Numerical simulations illustrate that Greenkhorn significantly outperforms the classical Sinkhorn algorithm in practice.

Minimax Rates and Efficient Algorithms for Noisy Sorting

There has been a recent surge of interest in studying permutation-based models for ranking from pairwise comparison data. Despite being structurally richer and more robust than parametric ranking models, permutation-based models are less well understood statistically and generally lack efficient learning algorithms. In this work, we study a prototype of permutation-based ranking models, namely, the noisy sorting model. We establish the optimal rates of learning the model under two sampling procedures. Furthermore, we provide a fast algorithm to achieve near-optimal rates if the observations are sampled independently. Along the way, we discover properties of the symmetric group which are of theoretical interest.

Online learning in repeated auctions

Motivated by online advertising auctions, we consider repeated Vickrey auctions where goods of unknown value are sold sequentially and bidders only learn (potentially noisy) information about a good's value once it is purchased. We adopt an online learning approach with bandit feedback to model this problem and derive bidding strategies for two models: stochastic and adversarial. In the stochastic model, the observed values of the goods are random variables centered around the true value of the good. In this case, logarithmic regret is achievable when competing against well behaved adversaries. In the adversarial model, the goods need not be identical and we simply compare our performance against that of the best fixed bid in hindsight. We show that sublinear regret is also achievable in this case and prove matching minimax lower bounds. To our knowledge, this is the first complete set of strategies for bidders participating in auctions of this type.