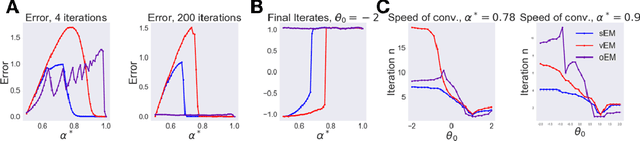
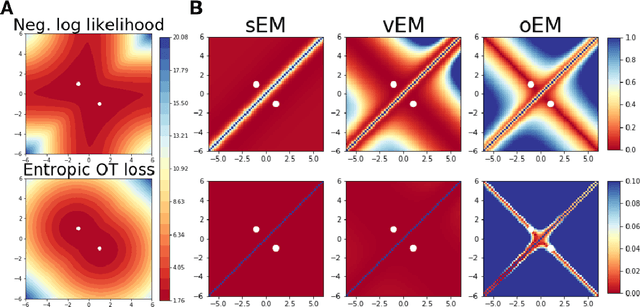
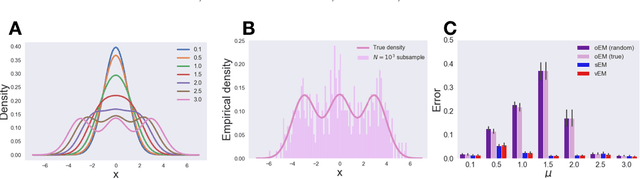
Sinkhorn EM: An Expectation-Maximization algorithm based on entropic optimal transport

We study Sinkhorn EM (sEM), a variant of the expectation maximization (EM) algorithm for mixtures based on entropic optimal transport. sEM differs from the classic EM algorithm in the way responsibilities are computed during the expectation step: rather than assign data points to clusters independently, sEM uses optimal transport to compute responsibilities by incorporating prior information about mixing weights. Like EM, sEM has a natural interpretation as a coordinate ascent procedure, which iteratively constructs and optimizes a lower bound on the log-likelihood. However, we show theoretically and empirically that sEM has better behavior than EM: it possesses better global convergence guarantees and is less prone to getting stuck in bad local optima. We complement these findings with experiments on simulated data as well as in an inference task involving C. elegans neurons and show that sEM learns cell labels significantly better than other approaches.

Statistical bounds for entropic optimal transport: sample complexity and the central limit theorem

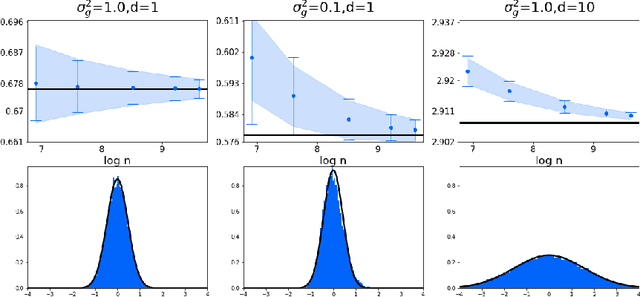
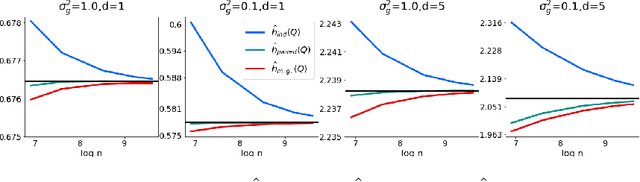
We prove several fundamental statistical bounds for entropic OT with the squared Euclidean cost between subgaussian probability measures in arbitrary dimension. First, through a new sample complexity result we establish the rate of convergence of entropic OT for empirical measures. Our analysis improves exponentially on the bound of Genevay et al. (2019) and extends their work to unbounded measures. Second, we establish a central limit theorem for entropic OT, based on techniques developed by Del Barrio and Loubes (2019). Previously, such a result was only known for finite metric spaces. As an application of our results, we develop and analyze a new technique for estimating the entropy of a random variable corrupted by gaussian noise.

Learning Latent Permutations with Gumbel-Sinkhorn Networks

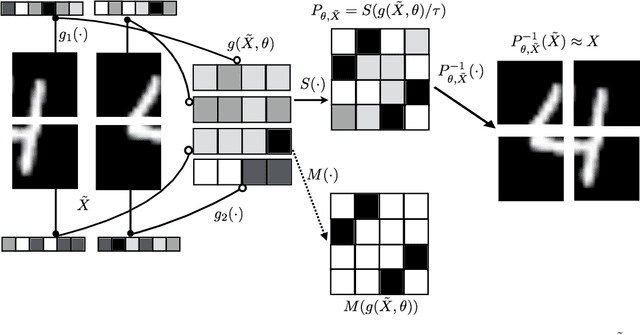
Permutations and matchings are core building blocks in a variety of latent variable models, as they allow us to align, canonicalize, and sort data. Learning in such models is difficult, however, because exact marginalization over these combinatorial objects is intractable. In response, this paper introduces a collection of new methods for end-to-end learning in such models that approximate discrete maximum-weight matching using the continuous Sinkhorn operator. Sinkhorn iteration is attractive because it functions as a simple, easy-to-implement analog of the softmax operator. With this, we can define the Gumbel-Sinkhorn method, an extension of the Gumbel-Softmax method (Jang et al. 2016, Maddison2016 et al. 2016) to distributions over latent matchings. We demonstrate the effectiveness of our method by outperforming competitive baselines on a range of qualitatively different tasks: sorting numbers, solving jigsaw puzzles, and identifying neural signals in worms.