Sinkhorn EM: An Expectation-Maximization algorithm based on entropic optimal transport
Paper and Code
Jun 30, 2020
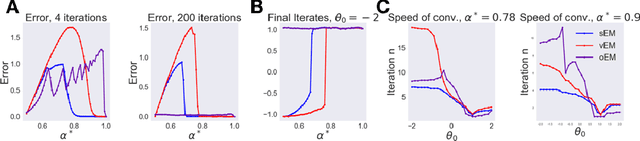
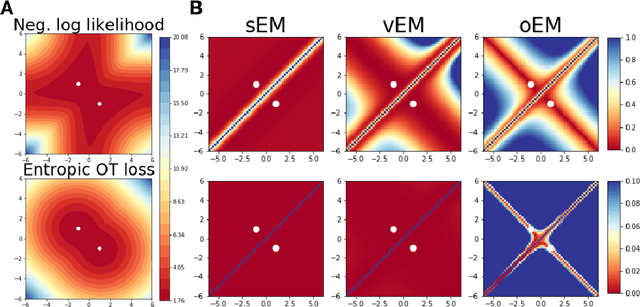
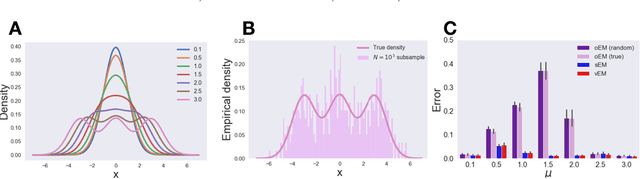
We study Sinkhorn EM (sEM), a variant of the expectation maximization (EM) algorithm for mixtures based on entropic optimal transport. sEM differs from the classic EM algorithm in the way responsibilities are computed during the expectation step: rather than assign data points to clusters independently, sEM uses optimal transport to compute responsibilities by incorporating prior information about mixing weights. Like EM, sEM has a natural interpretation as a coordinate ascent procedure, which iteratively constructs and optimizes a lower bound on the log-likelihood. However, we show theoretically and empirically that sEM has better behavior than EM: it possesses better global convergence guarantees and is less prone to getting stuck in bad local optima. We complement these findings with experiments on simulated data as well as in an inference task involving C. elegans neurons and show that sEM learns cell labels significantly better than other approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge