Modeling Neural Activity with Conditionally Linear Dynamical Systems

Neural population activity exhibits complex, nonlinear dynamics, varying in time, over trials, and across experimental conditions. Here, we develop Conditionally Linear Dynamical System (CLDS) models as a general-purpose method to characterize these dynamics. These models use Gaussian Process (GP) priors to capture the nonlinear dependence of circuit dynamics on task and behavioral variables. Conditioned on these covariates, the data is modeled with linear dynamics. This allows for transparent interpretation and tractable Bayesian inference. We find that CLDS models can perform well even in severely data-limited regimes (e.g. one trial per condition) due to their Bayesian formulation and ability to share statistical power across nearby task conditions. In example applications, we apply CLDS to model thalamic neurons that nonlinearly encode heading direction and to model motor cortical neurons during a cued reaching task

Comparing noisy neural population dynamics using optimal transport distances

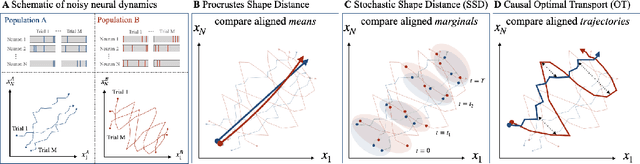
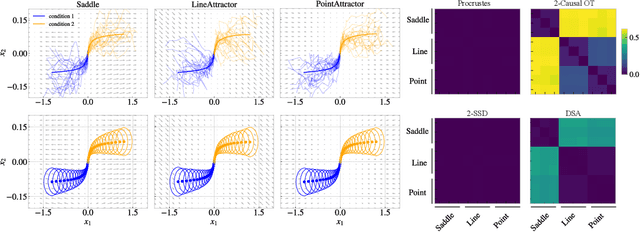
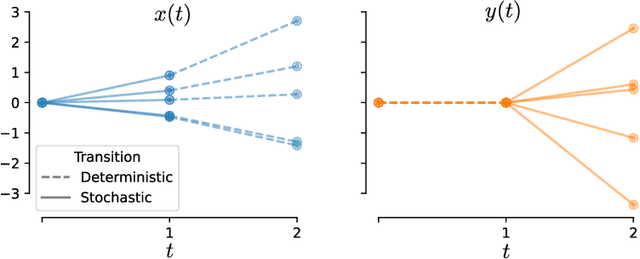
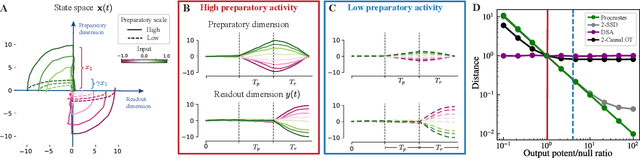
Biological and artificial neural systems form high-dimensional neural representations that underpin their computational capabilities. Methods for quantifying geometric similarity in neural representations have become a popular tool for identifying computational principles that are potentially shared across neural systems. These methods generally assume that neural responses are deterministic and static. However, responses of biological systems, and some artificial systems, are noisy and dynamically unfold over time. Furthermore, these characteristics can have substantial influence on a system's computational capabilities. Here, we demonstrate that existing metrics can fail to capture key differences between neural systems with noisy dynamic responses. We then propose a metric for comparing the geometry of noisy neural trajectories, which can be derived as an optimal transport distance between Gaussian processes. We use the metric to compare models of neural responses in different regions of the motor system and to compare the dynamics of latent diffusion models for text-to-image synthesis.

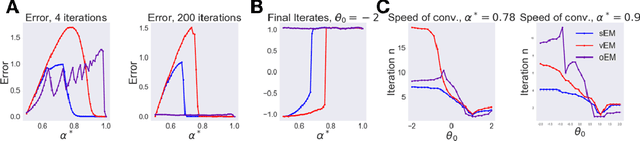
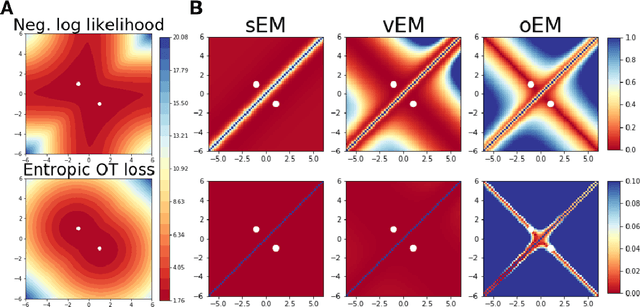
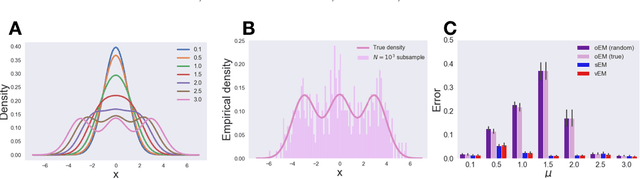
Sinkhorn EM: An Expectation-Maximization algorithm based on entropic optimal transport

We study Sinkhorn EM (sEM), a variant of the expectation maximization (EM) algorithm for mixtures based on entropic optimal transport. sEM differs from the classic EM algorithm in the way responsibilities are computed during the expectation step: rather than assign data points to clusters independently, sEM uses optimal transport to compute responsibilities by incorporating prior information about mixing weights. Like EM, sEM has a natural interpretation as a coordinate ascent procedure, which iteratively constructs and optimizes a lower bound on the log-likelihood. However, we show theoretically and empirically that sEM has better behavior than EM: it possesses better global convergence guarantees and is less prone to getting stuck in bad local optima. We complement these findings with experiments on simulated data as well as in an inference task involving C. elegans neurons and show that sEM learns cell labels significantly better than other approaches.

Temporal Wasserstein non-negative matrix factorization for non-rigid motion segmentation and spatiotemporal deconvolution

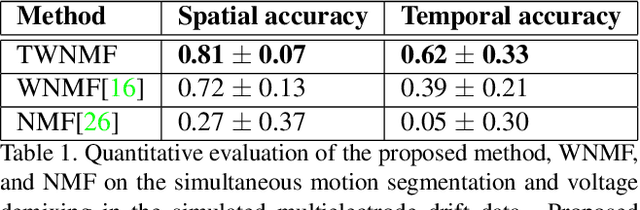
Motion segmentation for natural images commonly relies on dense optic flow to yield point trajectories which can be grouped into clusters through various means including spectral clustering or minimum cost multicuts. However, in biological imaging scenarios, such as fluorescence microscopy or calcium imaging, where the signal to noise ratio is compromised and intensity fluctuations occur, optical flow may be difficult to approximate. To this end, we propose an alternative paradigm for motion segmentation based on optimal transport which models the video frames as time-varying mass represented as histograms. Thus, we cast motion segmentation as a temporal non-linear matrix factorization problem with Wasserstein metric loss. The dictionary elements of this factorization yield segmentation of motion into coherent objects while the loading coefficients allow for time-varying intensity signal of the moving objects to be captured. We demonstrate the use of the proposed paradigm on a simulated multielectrode drift scenario, as well as calcium indicating fluorescence microscopy videos of the nematode Caenorhabditis elegans (C. elegans). The latter application has the added utility of extracting neural activity of the animal in freely conducted behavior.

Wasserstein total variation filtering

In this paper, we expand upon the theory of trend filtering by introducing the use of the Wasserstein metric as a means to control the amount of spatiotemporal variation in filtered time series data. While trend filtering utilizes regularization to produce signal estimates that are piecewise linear, in the case of $\ell_1$ regularization, or temporally smooth, in the case of $\ell_2$ regularization, it ignores the topology of the spatial distribution of signal. By incorporating the information about the underlying metric space of the pixel layout, the Wasserstein metric is an attractive choice as a regularizer to undercover spatiotemporal trends in time series data. We introduce a globally optimal algorithm for efficiently estimating the filtered signal under a Wasserstein finite differences operator. The efficacy of the proposed algorithm in preserving spatiotemporal trends in time series video is demonstrated in both simulated and fluorescent microscopy videos of the nematode caenorhabditis elegans and compared against standard trend filtering algorithms.

Robust approximate linear regression without correspondence

Estimating regression coefficients using unordered multisets of covariates and responses has been introduced as the regression without correspondence problem. Previous theoretical analysis of the problem has been done in a setting where the responses are a permutation of the regressed covariates. This paper expands the setting by analyzing the problem where they may be missing correspondences and outliers in addition to a permutation action. We term this problem robust regression without correspondence and provide several algorithms for exact and approximate recovery in a noiseless and noisy one-dimensional setting as well as an approximation algorithm for multiple dimensions. The theoretical guarantees of the algorithms are verified in simulation data. We also demonstrate a neuroscience application by obtaining robust point set matchings of the neurons of the model organism Caenorhabditis elegans.