Comparing noisy neural population dynamics using optimal transport distances

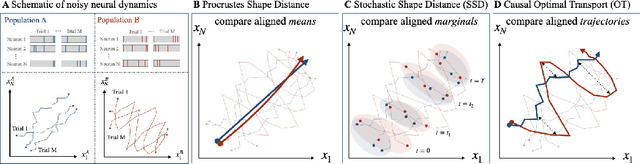
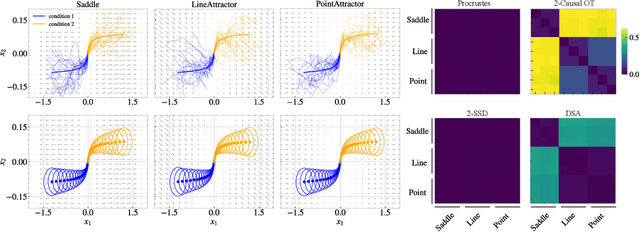
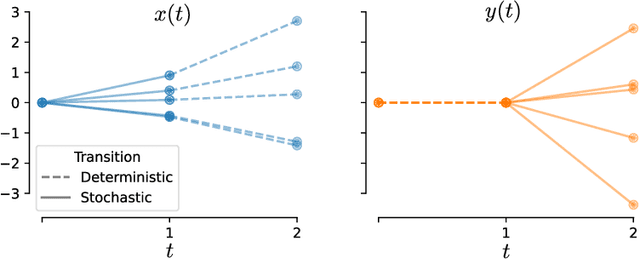
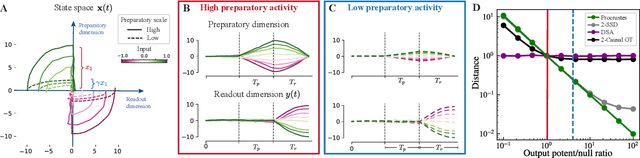
Biological and artificial neural systems form high-dimensional neural representations that underpin their computational capabilities. Methods for quantifying geometric similarity in neural representations have become a popular tool for identifying computational principles that are potentially shared across neural systems. These methods generally assume that neural responses are deterministic and static. However, responses of biological systems, and some artificial systems, are noisy and dynamically unfold over time. Furthermore, these characteristics can have substantial influence on a system's computational capabilities. Here, we demonstrate that existing metrics can fail to capture key differences between neural systems with noisy dynamic responses. We then propose a metric for comparing the geometry of noisy neural trajectories, which can be derived as an optimal transport distance between Gaussian processes. We use the metric to compare models of neural responses in different regions of the motor system and to compare the dynamics of latent diffusion models for text-to-image synthesis.

What Representational Similarity Measures Imply about Decodable Information

Neural responses encode information that is useful for a variety of downstream tasks. A common approach to understand these systems is to build regression models or ``decoders'' that reconstruct features of the stimulus from neural responses. Popular neural network similarity measures like centered kernel alignment (CKA), canonical correlation analysis (CCA), and Procrustes shape distance, do not explicitly leverage this perspective and instead highlight geometric invariances to orthogonal or affine transformations when comparing representations. Here, we show that many of these measures can, in fact, be equivalently motivated from a decoding perspective. Specifically, measures like CKA and CCA quantify the average alignment between optimal linear readouts across a distribution of decoding tasks. We also show that the Procrustes shape distance upper bounds the distance between optimal linear readouts and that the converse holds for representations with low participation ratio. Overall, our work demonstrates a tight link between the geometry of neural representations and the ability to linearly decode information. This perspective suggests new ways of measuring similarity between neural systems and also provides novel, unifying interpretations of existing measures.

Discriminating image representations with principal distortions

Image representations (artificial or biological) are often compared in terms of their global geometry; however, representations with similar global structure can have strikingly different local geometries. Here, we propose a framework for comparing a set of image representations in terms of their local geometries. We quantify the local geometry of a representation using the Fisher information matrix, a standard statistical tool for characterizing the sensitivity to local stimulus distortions, and use this as a substrate for a metric on the local geometry in the vicinity of a base image. This metric may then be used to optimally differentiate a set of models, by finding a pair of "principal distortions" that maximize the variance of the models under this metric. We use this framework to compare a set of simple models of the early visual system, identifying a novel set of image distortions that allow immediate comparison of the models by visual inspection. In a second example, we apply our method to a set of deep neural network models and reveal differences in the local geometry that arise due to architecture and training types. These examples highlight how our framework can be used to probe for informative differences in local sensitivities between complex computational models, and suggest how it could be used to compare model representations with human perception.

Neuronal Temporal Filters as Normal Mode Extractors

To generate actions in the face of physiological delays, the brain must predict the future. Here we explore how prediction may lie at the core of brain function by considering a neuron predicting the future of a scalar time series input. Assuming that the dynamics of the lag vector (a vector composed of several consecutive elements of the time series) are locally linear, Normal Mode Decomposition decomposes the dynamics into independently evolving (eigen-)modes allowing for straightforward prediction. We propose that a neuron learns the top mode and projects its input onto the associated subspace. Under this interpretation, the temporal filter of a neuron corresponds to the left eigenvector of a generalized eigenvalue problem. We mathematically analyze the operation of such an algorithm on noisy observations of synthetic data generated by a linear system. Interestingly, the shape of the temporal filter varies with the signal-to-noise ratio (SNR): a noisy input yields a monophasic filter and a growing SNR leads to multiphasic filters with progressively greater number of phases. Such variation in the temporal filter with input SNR resembles that observed experimentally in biological neurons.

Adaptive whitening with fast gain modulation and slow synaptic plasticity

Neurons in early sensory areas rapidly adapt to changing sensory statistics, both by normalizing the variance of their individual responses and by reducing correlations between their responses. Together, these transformations may be viewed as an adaptive form of statistical whitening. Existing mechanistic models of adaptive whitening exclusively use either synaptic plasticity or gain modulation as the biological substrate for adaptation; however, on their own, each of these models has significant limitations. In this work, we unify these approaches in a normative multi-timescale mechanistic model that adaptively whitens its responses with complementary computational roles for synaptic plasticity and gain modulation. Gains are modified on a fast timescale to adapt to the current statistical context, whereas synapses are modified on a slow timescale to learn structural properties of the input statistics that are invariant across contexts. Our model is derived from a novel multi-timescale whitening objective that factorizes the inverse whitening matrix into basis vectors, which correspond to synaptic weights, and a diagonal matrix, which corresponds to neuronal gains. We test our model on synthetic and natural datasets and find that the synapses learn optimal configurations over long timescales that enable the circuit to adaptively whiten neural responses on short timescales exclusively using gain modulation.

A normative framework for deriving neural networks with multi-compartmental neurons and non-Hebbian plasticity

An established normative approach for understanding the algorithmic basis of neural computation is to derive online algorithms from principled computational objectives and evaluate their compatibility with anatomical and physiological observations. Similarity matching objectives have served as successful starting points for deriving online algorithms that map onto neural networks (NNs) with point neurons and Hebbian/anti-Hebbian plasticity. These NN models account for many anatomical and physiological observations; however, the objectives have limited computational power and the derived NNs do not explain multi-compartmental neuronal structures and non-Hebbian forms of plasticity that are prevalent throughout the brain. In this article, we review and unify recent extensions of the similarity matching approach to address more complex objectives, including a broad range of unsupervised and self-supervised learning tasks that can be formulated as generalized eigenvalue problems or nonnegative matrix factorization problems. Interestingly, the online algorithms derived from these objectives naturally map onto NNs with multi-compartmental neurons and local, non-Hebbian learning rules. Therefore, this unified extension of the similarity matching approach provides a normative framework that facilitates understanding the multi-compartmental neuronal structures and non-Hebbian plasticity found throughout the brain.

Statistical whitening of neural populations with gain-modulating interneurons

Statistical whitening transformations play a fundamental role in many computational systems, and may also play an important role in biological sensory systems. Individual neurons appear to rapidly and reversibly alter their input-output gains, approximately normalizing the variance of their responses. Populations of neurons appear to regulate their joint responses, reducing correlations between neural activities. It is natural to see whitening as the objective that guides these behaviors, but the mechanism for such joint changes is unknown, and direct adjustment of synaptic interactions would seem to be both too slow, and insufficiently reversible. Motivated by the extensive neuroscience literature on rapid gain modulation, we propose a recurrent network architecture in which joint whitening is achieved through modulation of gains within the circuit. Specifically, we derive an online statistical whitening algorithm that regulates the joint second-order statistics of a multi-dimensional input by adjusting the marginal variances of an overcomplete set of interneuron projections. The gains of these interneurons are adjusted individually, using only local signals, and feed back onto the primary neurons. The network converges to a state in which the responses of the primary neurons are whitened. We demonstrate through simulations that the behavior of the network is robust to poor conditioning or noise when the gains are sign-constrained, and can be generalized to achieve a form of local whitening in convolutional populations, such as those found throughout the visual or auditory system.

An online algorithm for contrastive Principal Component Analysis

Finding informative low-dimensional representations that can be computed efficiently in large datasets is an important problem in data analysis. Recently, contrastive Principal Component Analysis (cPCA) was proposed as a more informative generalization of PCA that takes advantage of contrastive learning. However, the performance of cPCA is sensitive to hyper-parameter choice and there is currently no online algorithm for implementing cPCA. Here, we introduce a modified cPCA method, which we denote cPCA*, that is more interpretable and less sensitive to the choice of hyper-parameter. We derive an online algorithm for cPCA* and show that it maps onto a neural network with local learning rules, so it can potentially be implemented in energy efficient neuromorphic hardware. We evaluate the performance of our online algorithm on real datasets and highlight the differences and similarities with the original formulation.

Interneurons accelerate learning dynamics in recurrent neural networks for statistical adaptation

Early sensory systems in the brain rapidly adapt to fluctuating input statistics, which requires recurrent communication between neurons. Mechanistically, such recurrent communication is often indirect and mediated by local interneurons. In this work, we explore the computational benefits of mediating recurrent communication via interneurons compared with direct recurrent connections. To this end, we consider two mathematically tractable recurrent neural networks that statistically whiten their inputs -- one with direct recurrent connections and the other with interneurons that mediate recurrent communication. By analyzing the corresponding continuous synaptic dynamics and numerically simulating the networks, we show that the network with interneurons is more robust to initialization than the network with direct recurrent connections in the sense that the convergence time for the synaptic dynamics in the network with interneurons (resp. direct recurrent connections) scales logarithmically (resp. linearly) with the spectrum of their initialization. Our results suggest that interneurons are computationally useful for rapid adaptation to changing input statistics. Interestingly, the network with interneurons is an overparameterized solution of the whitening objective for the network with direct recurrent connections, so our results can be viewed as a recurrent neural network analogue of the implicit acceleration phenomenon observed in overparameterized feedforward linear networks.

A biologically plausible neural network for local supervision in cortical microcircuits

The backpropagation algorithm is an invaluable tool for training artificial neural networks; however, because of a weight sharing requirement, it does not provide a plausible model of brain function. Here, in the context of a two-layer network, we derive an algorithm for training a neural network which avoids this problem by not requiring explicit error computation and backpropagation. Furthermore, our algorithm maps onto a neural network that bears a remarkable resemblance to the connectivity structure and learning rules of the cortex. We find that our algorithm empirically performs comparably to backprop on a number of datasets.