Modeling Neural Activity with Conditionally Linear Dynamical Systems

Neural population activity exhibits complex, nonlinear dynamics, varying in time, over trials, and across experimental conditions. Here, we develop Conditionally Linear Dynamical System (CLDS) models as a general-purpose method to characterize these dynamics. These models use Gaussian Process (GP) priors to capture the nonlinear dependence of circuit dynamics on task and behavioral variables. Conditioned on these covariates, the data is modeled with linear dynamics. This allows for transparent interpretation and tractable Bayesian inference. We find that CLDS models can perform well even in severely data-limited regimes (e.g. one trial per condition) due to their Bayesian formulation and ability to share statistical power across nearby task conditions. In example applications, we apply CLDS to model thalamic neurons that nonlinearly encode heading direction and to model motor cortical neurons during a cued reaching task

Spectral learning of Bernoulli linear dynamical systems models for decision-making

Latent linear dynamical systems with Bernoulli observations provide a powerful modeling framework for identifying the temporal dynamics underlying binary time series data, which arise in a variety of contexts such as binary decision-making and discrete stochastic processes such as binned neural spike trains. Here, we develop a spectral learning method for fast, efficient fitting of Bernoulli latent linear dynamical system (LDS) models. Our approach extends traditional subspace identification methods to the Bernoulli setting via a transformation of the first and second sample moments. This results in a robust, fixed-cost estimator that avoids the hazards of local optima and the long computation time of iterative fitting procedures like the expectation-maximization (EM) algorithm. In regimes where data is limited or assumptions about the statistical structure of the data are not met, we demonstrate that the spectral estimate provides a good initialization for Laplace-EM fitting. Finally, we show that the estimator provides substantial benefits to real world settings by analyzing data from mice performing a sensory decision-making task.

Bayesian Active Learning for Discrete Latent Variable Models

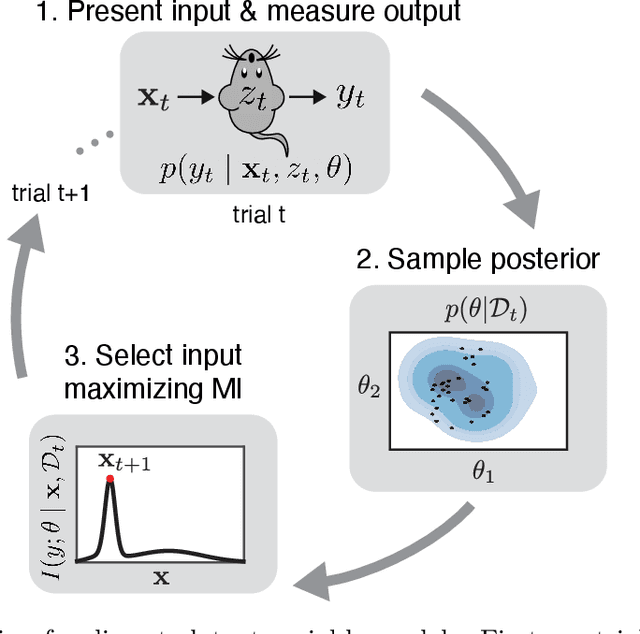
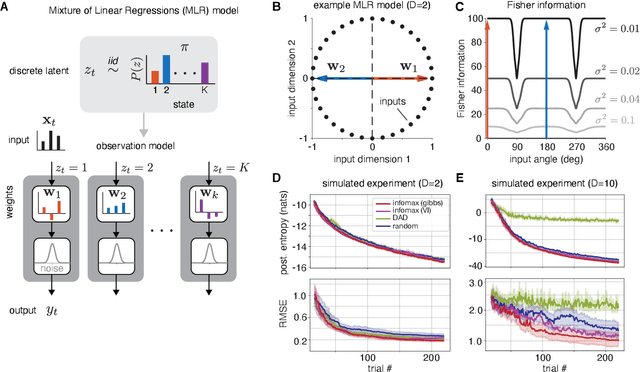
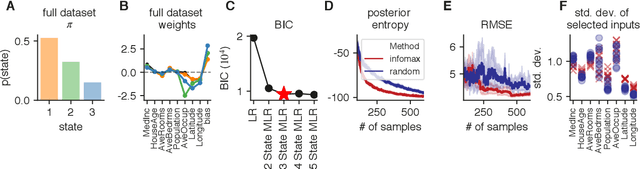
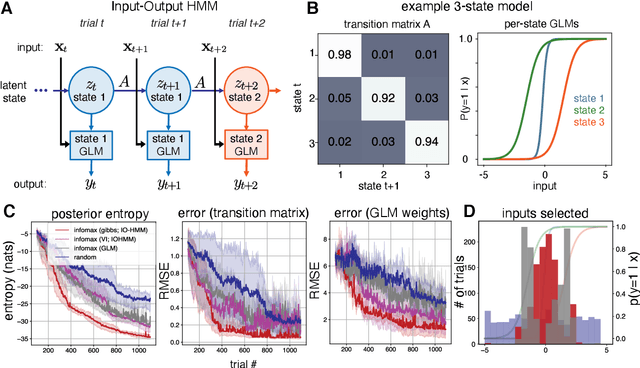
Active learning seeks to reduce the number of samples required to estimate the parameters of a model, thus forming an important class of techniques in modern machine learning. However, past work on active learning has largely overlooked latent variable models, which play a vital role in neuroscience, psychology, and a variety of other engineering and scientific disciplines. Here we address this gap in the literature and propose a novel framework for maximum-mutual-information input selection for learning discrete latent variable regression models. We first examine a class of models known as "mixtures of linear regressions" (MLR). This example is striking because it is well known that active learning confers no advantage for standard least-squares regression. However, we show -- both in simulations and analytically using Fisher information -- that optimal input selection can nevertheless provide dramatic gains for mixtures of regression models; we also validate this on a real-world application of MLRs. We then consider a powerful class of temporally structured latent variable models known as Input-Output Hidden Markov Models (IO-HMMs), which have recently gained prominence in neuroscience. We show that our method substantially speeds up learning, and outperforms a variety of approximate methods based on variational and amortized inference.

Loss-calibrated expectation propagation for approximate Bayesian decision-making

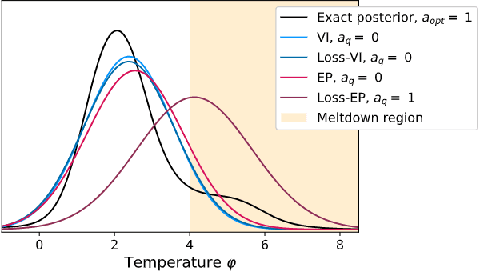
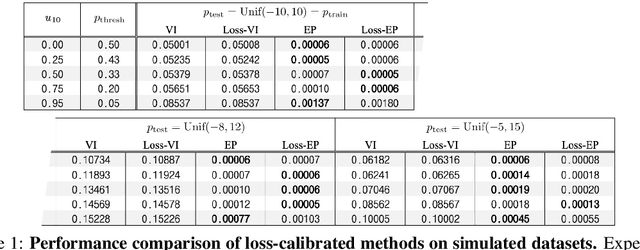
Approximate Bayesian inference methods provide a powerful suite of tools for finding approximations to intractable posterior distributions. However, machine learning applications typically involve selecting actions, which -- in a Bayesian setting -- depend on the posterior distribution only via its contribution to expected utility. A growing body of work on loss-calibrated approximate inference methods has therefore sought to develop posterior approximations sensitive to the influence of the utility function. Here we introduce loss-calibrated expectation propagation (Loss-EP), a loss-calibrated variant of expectation propagation. This method resembles standard EP with an additional factor that "tilts" the posterior towards higher-utility decisions. We show applications to Gaussian process classification under binary utility functions with asymmetric penalties on False Negative and False Positive errors, and show how this asymmetry can have dramatic consequences on what information is "useful" to capture in an approximation.

High-contrast "gaudy" images improve the training of deep neural network models of visual cortex

A key challenge in understanding the sensory transformations of the visual system is to obtain a highly predictive model of responses from visual cortical neurons. Deep neural networks (DNNs) provide a promising candidate for such a model. However, DNNs require orders of magnitude more training data than neuroscientists can collect from real neurons because experimental recording time is severely limited. This motivates us to find images that train highly-predictive DNNs with as little training data as possible. We propose gaudy images---high-contrast binarized versions of natural images---to efficiently train DNNs. In extensive simulation experiments, we find that training DNNs with gaudy images substantially reduces the number of training images needed to accurately predict the simulated responses of visual cortical neurons. We also find that gaudy images, chosen before training, outperform images chosen during training by active learning algorithms. Thus, gaudy images overemphasize features of natural images, especially edges, that are the most important for efficiently training DNNs. We believe gaudy images will aid in the modeling of visual cortical neurons, potentially opening new scientific questions about visual processing, as well as aid general practitioners that seek ways to improve the training of DNNs.

Unifying and generalizing models of neural dynamics during decision-making

An open question in systems and computational neuroscience is how neural circuits accumulate evidence towards a decision. Fitting models of decision-making theory to neural activity helps answer this question, but current approaches limit the number of these models that we can fit to neural data. Here we propose a unifying framework for modeling neural activity during decision-making tasks. The framework includes the canonical drift-diffusion model and enables extensions such as multi-dimensional accumulators, variable and collapsing boundaries, and discrete jumps. Our framework is based on constraining the parameters of recurrent state-space models, for which we introduce a scalable variational Laplace-EM inference algorithm. We applied the modeling approach to spiking responses recorded from monkey parietal cortex during two decision-making tasks. We found that a two-dimensional accumulator better captured the trial-averaged responses of a set of parietal neurons than a single accumulator model. Next, we identified a variable lower boundary in the responses of an LIP neuron during a random dot motion task.

Efficient non-conjugate Gaussian process factor models for spike count data using polynomial approximations

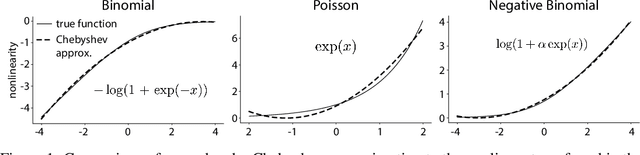
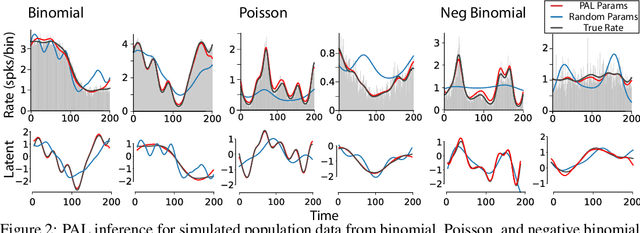
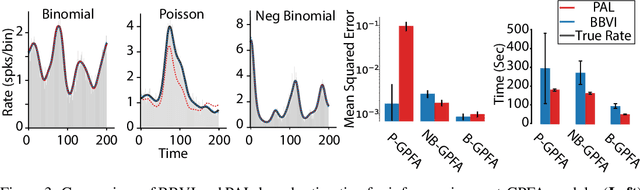
Gaussian Process Factor Analysis (GPFA) has been broadly applied to the problem of identifying smooth, low-dimensional temporal structure underlying large-scale neural recordings. However, spike trains are non-Gaussian, which motivates combining GPFA with discrete observation models for binned spike count data. The drawback to this approach is that GPFA priors are not conjugate to count model likelihoods, which makes inference challenging. Here we address this obstacle by introducing a fast, approximate inference method for non-conjugate GPFA models. Our approach uses orthogonal second-order polynomials to approximate the nonlinear terms in the non-conjugate log-likelihood, resulting in a method we refer to as polynomial approximate log-likelihood (PAL) estimators. This approximation allows for accurate closed-form evaluation of marginal likelihood and fast numerical optimization for parameters and hyperparameters. We derive PAL estimators for GPFA models with binomial, Poisson, and negative binomial observations, and additionally show that the parameters obtained can be used to initialize black-box variational inference, which significantly speeds up and stabilizes the inference procedure for these factor analytic models. We apply these methods to data from mouse visual cortex and monkey higher-order visual and parietal cortices, and compare GPFA under three different spike count observation models to traditional GPFA. We demonstrate that PAL estimators achieve fast and accurate extraction of latent structure from multi-neuron spike train data.

Shared Representational Geometry Across Neural Networks

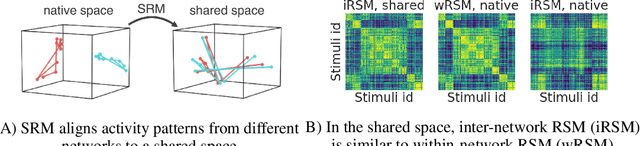
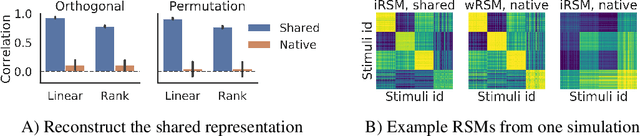
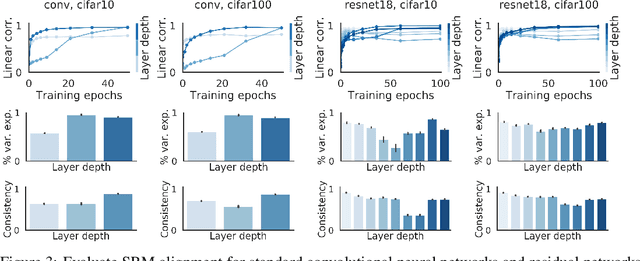
Different neural networks trained on the same dataset often learn similar input-output mappings with very different weights. Is there some correspondence between these neural network solutions? For linear networks, it has been shown that different instances of the same network architecture encode the same representational similarity matrix, and their neural activity patterns are connected by orthogonal transformations. However, it is unclear if this holds for non-linear networks. Using a shared response model, we show that different neural networks encode the same input examples as different orthogonal transformations of an underlying shared representation. We test this claim using both standard convolutional neural networks and residual networks on CIFAR10 and CIFAR100.

Exploiting gradients and Hessians in Bayesian optimization and Bayesian quadrature

An exciting branch of machine learning research focuses on methods for learning, optimizing, and integrating unknown functions that are difficult or costly to evaluate. A popular Bayesian approach to this problem uses a Gaussian process (GP) to construct a posterior distribution over the function of interest given a set of observed measurements, and selects new points to evaluate using the statistics of this posterior. Here we extend these methods to exploit derivative information from the unknown function. We describe methods for Bayesian optimization (BO) and Bayesian quadrature (BQ) in settings where first and second derivatives may be evaluated along with the function itself. We perform sampling-based inference in order to incorporate uncertainty over hyperparameters, and show that both hyperparameter and function uncertainty decrease much more rapidly when using derivative information. Moreover, we introduce techniques for overcoming ill-conditioning issues that have plagued earlier methods for gradient-enhanced Gaussian processes and kriging. We illustrate the efficacy of these methods using applications to real and simulated Bayesian optimization and quadrature problems, and show that exploting derivatives can provide substantial gains over standard methods.

Dependent relevance determination for smooth and structured sparse regression

In many problem settings, parameter vectors are not merely sparse, but dependent in such a way that non-zero coefficients tend to cluster together. We refer to this form of dependency as "region sparsity". Classical sparse regression methods, such as the lasso and automatic relevance determination (ARD), which model parameters as independent a priori, and therefore do not exploit such dependencies. Here we introduce a hierarchical model for smooth, region-sparse weight vectors and tensors in a linear regression setting. Our approach represents a hierarchical extension of the relevance determination framework, where we add a transformed Gaussian process to model the dependencies between the prior variances of regression weights. We combine this with a structured model of the prior variances of Fourier coefficients, which eliminates unnecessary high frequencies. The resulting prior encourages weights to be region-sparse in two different bases simultaneously. We develop Laplace approximation and Monte Carlo Markov Chain (MCMC) sampling to provide efficient inference for the posterior. Furthermore, a two-stage convex relaxation of the Laplace approximation approach is also provided to relax the inevitable non-convexity during the optimization. We finally show substantial improvements over comparable methods for both simulated and real datasets from brain imaging.