Meta-Dynamical State Space Models for Integrative Neural Data Analysis

Learning shared structure across environments facilitates rapid learning and adaptive behavior in neural systems. This has been widely demonstrated and applied in machine learning to train models that are capable of generalizing to novel settings. However, there has been limited work exploiting the shared structure in neural activity during similar tasks for learning latent dynamics from neural recordings. Existing approaches are designed to infer dynamics from a single dataset and cannot be readily adapted to account for statistical heterogeneities across recordings. In this work, we hypothesize that similar tasks admit a corresponding family of related solutions and propose a novel approach for meta-learning this solution space from task-related neural activity of trained animals. Specifically, we capture the variabilities across recordings on a low-dimensional manifold which concisely parametrizes this family of dynamics, thereby facilitating rapid learning of latent dynamics given new recordings. We demonstrate the efficacy of our approach on few-shot reconstruction and forecasting of synthetic dynamical systems, and neural recordings from the motor cortex during different arm reaching tasks.

Back to the Continuous Attractor

Continuous attractors offer a unique class of solutions for storing continuous-valued variables in recurrent system states for indefinitely long time intervals. Unfortunately, continuous attractors suffer from severe structural instability in general--they are destroyed by most infinitesimal changes of the dynamical law that defines them. This fragility limits their utility especially in biological systems as their recurrent dynamics are subject to constant perturbations. We observe that the bifurcations from continuous attractors in theoretical neuroscience models display various structurally stable forms. Although their asymptotic behaviors to maintain memory are categorically distinct, their finite-time behaviors are similar. We build on the persistent manifold theory to explain the commonalities between bifurcations from and approximations of continuous attractors. Fast-slow decomposition analysis uncovers the persistent manifold that survives the seemingly destructive bifurcation. Moreover, recurrent neural networks trained on analog memory tasks display approximate continuous attractors with predicted slow manifold structures. Therefore, continuous attractors are functionally robust and remain useful as a universal analogy for understanding analog memory.

Large-scale variational Gaussian state-space models

We introduce an amortized variational inference algorithm and structured variational approximation for state-space models with nonlinear dynamics driven by Gaussian noise. Importantly, the proposed framework allows for efficient evaluation of the ELBO and low-variance stochastic gradient estimates without resorting to diagonal Gaussian approximations by exploiting (i) the low-rank structure of Monte-Carlo approximations to marginalize the latent state through the dynamics (ii) an inference network that approximates the update step with low-rank precision matrix updates (iii) encoding current and future observations into pseudo observations -- transforming the approximate smoothing problem into an (easier) approximate filtering problem. Overall, the necessary statistics and ELBO can be computed in $O(TL(Sr + S^2 + r^2))$ time where $T$ is the series length, $L$ is the state-space dimensionality, $S$ are the number of samples used to approximate the predict step statistics, and $r$ is the rank of the approximate precision matrix update in the update step (which can be made of much lower dimension than $L$).

Persistent learning signals and working memory without continuous attractors

Neural dynamical systems with stable attractor structures, such as point attractors and continuous attractors, are hypothesized to underlie meaningful temporal behavior that requires working memory. However, working memory may not support useful learning signals necessary to adapt to changes in the temporal structure of the environment. We show that in addition to the continuous attractors that are widely implicated, periodic and quasi-periodic attractors can also support learning arbitrarily long temporal relationships. Unlike the continuous attractors that suffer from the fine-tuning problem, the less explored quasi-periodic attractors are uniquely qualified for learning to produce temporally structured behavior. Our theory has broad implications for the design of artificial learning systems and makes predictions about observable signatures of biological neural dynamics that can support temporal dependence learning and working memory. Based on our theory, we developed a new initialization scheme for artificial recurrent neural networks that outperforms standard methods for tasks that require learning temporal dynamics. Moreover, we propose a robust recurrent memory mechanism for integrating and maintaining head direction without a ring attractor.

Linear Time GPs for Inferring Latent Trajectories from Neural Spike Trains

Latent Gaussian process (GP) models are widely used in neuroscience to uncover hidden state evolutions from sequential observations, mainly in neural activity recordings. While latent GP models provide a principled and powerful solution in theory, the intractable posterior in non-conjugate settings necessitates approximate inference schemes, which may lack scalability. In this work, we propose cvHM, a general inference framework for latent GP models leveraging Hida-Mat\'ern kernels and conjugate computation variational inference (CVI). With cvHM, we are able to perform variational inference of latent neural trajectories with linear time complexity for arbitrary likelihoods. The reparameterization of stationary kernels using Hida-Mat\'ern GPs helps us connect the latent variable models that encode prior assumptions through dynamical systems to those that encode trajectory assumptions through GPs. In contrast to previous work, we use bidirectional information filtering, leading to a more concise implementation. Furthermore, we employ the Whittle approximate likelihood to achieve highly efficient hyperparameter learning.

Real-Time Variational Method for Learning Neural Trajectory and its Dynamics

Latent variable models have become instrumental in computational neuroscience for reasoning about neural computation. This has fostered the development of powerful offline algorithms for extracting latent neural trajectories from neural recordings. However, despite the potential of real time alternatives to give immediate feedback to experimentalists, and enhance experimental design, they have received markedly less attention. In this work, we introduce the exponential family variational Kalman filter (eVKF), an online recursive Bayesian method aimed at inferring latent trajectories while simultaneously learning the dynamical system generating them. eVKF works for arbitrary likelihoods and utilizes the constant base measure exponential family to model the latent state stochasticity. We derive a closed-form variational analogue to the predict step of the Kalman filter which leads to a provably tighter bound on the ELBO compared to another online variational method. We validate our method on synthetic and real-world data, and, notably, show that it achieves competitive performance

Spectral learning of Bernoulli linear dynamical systems models for decision-making

Latent linear dynamical systems with Bernoulli observations provide a powerful modeling framework for identifying the temporal dynamics underlying binary time series data, which arise in a variety of contexts such as binary decision-making and discrete stochastic processes such as binned neural spike trains. Here, we develop a spectral learning method for fast, efficient fitting of Bernoulli latent linear dynamical system (LDS) models. Our approach extends traditional subspace identification methods to the Bernoulli setting via a transformation of the first and second sample moments. This results in a robust, fixed-cost estimator that avoids the hazards of local optima and the long computation time of iterative fitting procedures like the expectation-maximization (EM) algorithm. In regimes where data is limited or assumptions about the statistical structure of the data are not met, we demonstrate that the spectral estimate provides a good initialization for Laplace-EM fitting. Finally, we show that the estimator provides substantial benefits to real world settings by analyzing data from mice performing a sensory decision-making task.

Neural Latents Benchmark '21: Evaluating latent variable models of neural population activity

Advances in neural recording present increasing opportunities to study neural activity in unprecedented detail. Latent variable models (LVMs) are promising tools for analyzing this rich activity across diverse neural systems and behaviors, as LVMs do not depend on known relationships between the activity and external experimental variables. However, progress in latent variable modeling is currently impeded by a lack of standardization, resulting in methods being developed and compared in an ad hoc manner. To coordinate these modeling efforts, we introduce a benchmark suite for latent variable modeling of neural population activity. We curate four datasets of neural spiking activity from cognitive, sensory, and motor areas to promote models that apply to the wide variety of activity seen across these areas. We identify unsupervised evaluation as a common framework for evaluating models across datasets, and apply several baselines that demonstrate benchmark diversity. We release this benchmark through EvalAI. http://neurallatents.github.io

Hida-Matérn Kernel

We present the class of Hida-Mat\'ern kernels, which is the canonical family of covariance functions over the entire space of stationary Gauss-Markov Processes. It extends upon Mat\'ern kernels, by allowing for flexible construction of priors over processes with oscillatory components. Any stationary kernel, including the widely used squared-exponential and spectral mixture kernels, are either directly within this class or are appropriate asymptotic limits, demonstrating the generality of this class. Taking advantage of its Markovian nature we show how to represent such processes as state space models using only the kernel and its derivatives. In turn this allows us to perform Gaussian Process inference more efficiently and side step the usual computational burdens. We also show how exploiting special properties of the state space representation enables improved numerical stability in addition to further reductions of computational complexity.

On 1/n neural representation and robustness

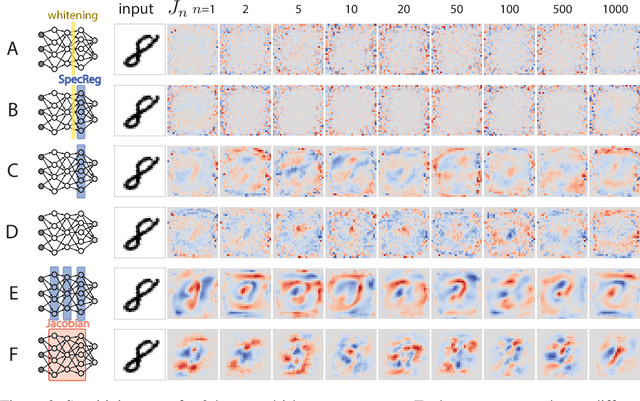
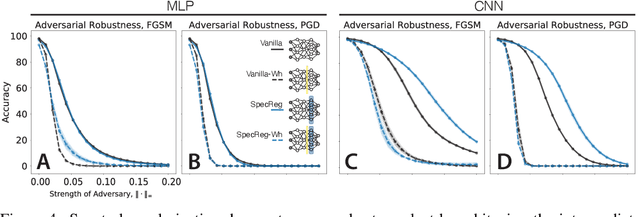
Understanding the nature of representation in neural networks is a goal shared by neuroscience and machine learning. It is therefore exciting that both fields converge not only on shared questions but also on similar approaches. A pressing question in these areas is understanding how the structure of the representation used by neural networks affects both their generalization, and robustness to perturbations. In this work, we investigate the latter by juxtaposing experimental results regarding the covariance spectrum of neural representations in the mouse V1 (Stringer et al) with artificial neural networks. We use adversarial robustness to probe Stringer et al's theory regarding the causal role of a 1/n covariance spectrum. We empirically investigate the benefits such a neural code confers in neural networks, and illuminate its role in multi-layer architectures. Our results show that imposing the experimentally observed structure on artificial neural networks makes them more robust to adversarial attacks. Moreover, our findings complement the existing theory relating wide neural networks to kernel methods, by showing the role of intermediate representations.