On 1/n neural representation and robustness

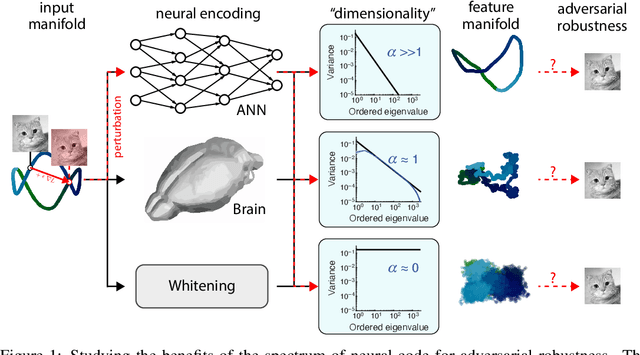
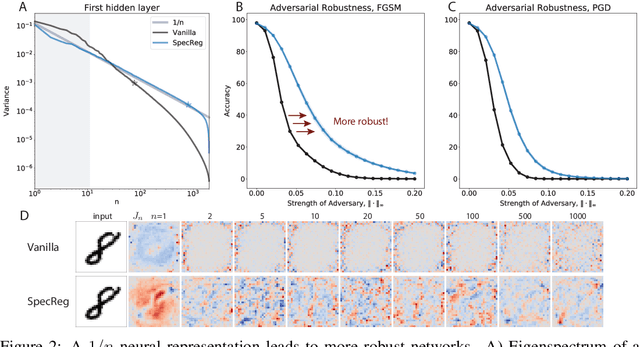
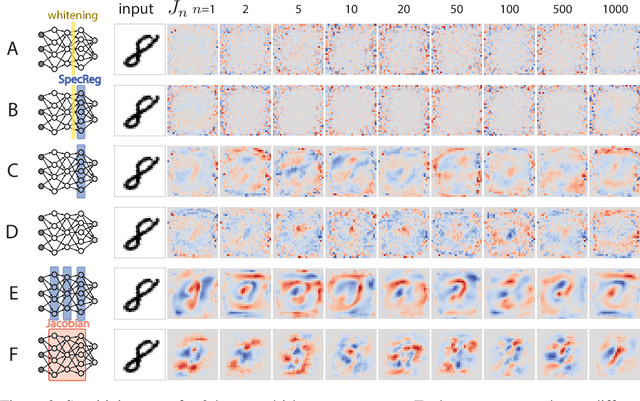
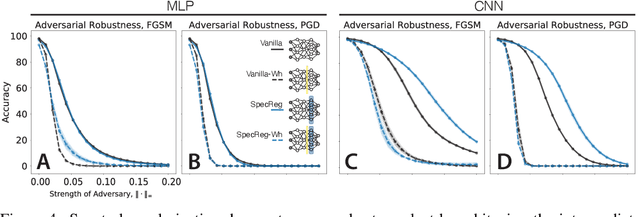
Understanding the nature of representation in neural networks is a goal shared by neuroscience and machine learning. It is therefore exciting that both fields converge not only on shared questions but also on similar approaches. A pressing question in these areas is understanding how the structure of the representation used by neural networks affects both their generalization, and robustness to perturbations. In this work, we investigate the latter by juxtaposing experimental results regarding the covariance spectrum of neural representations in the mouse V1 (Stringer et al) with artificial neural networks. We use adversarial robustness to probe Stringer et al's theory regarding the causal role of a 1/n covariance spectrum. We empirically investigate the benefits such a neural code confers in neural networks, and illuminate its role in multi-layer architectures. Our results show that imposing the experimentally observed structure on artificial neural networks makes them more robust to adversarial attacks. Moreover, our findings complement the existing theory relating wide neural networks to kernel methods, by showing the role of intermediate representations.

Characterizing the invariances of learning algorithms using category theory

Many learning algorithms have invariances: when their training data is transformed in certain ways, the function they learn transforms in a predictable manner. Here we formalize this notion using concepts from the mathematical field of category theory. The invariances that a supervised learning algorithm possesses are formalized by categories of predictor and target spaces, whose morphisms represent the algorithm's invariances, and an index category whose morphisms represent permutations of the training examples. An invariant learning algorithm is a natural transformation between two functors from the product of these categories to the category of sets, representing training datasets and learned functions respectively. We illustrate the framework by characterizing and contrasting the invariances of linear regression and ridge regression.

High-dimensional cluster analysis with the Masked EM Algorithm

Cluster analysis faces two problems in high dimensions: first, the `curse of dimensionality' that can lead to overfitting and poor generalization performance; and second, the sheer time taken for conventional algorithms to process large amounts of high-dimensional data. In many applications, only a small subset of features provide information about the cluster membership of any one data point, however this informative feature subset may not be the same for all data points. Here we introduce a `Masked EM' algorithm for fitting mixture of Gaussians models in such cases. We show that the algorithm performs close to optimally on simulated Gaussian data, and in an application of `spike sorting' of high channel-count neuronal recordings.