SueYeon Chung
Estimating Dimensionality of Neural Representations from Finite Samples
Sep 30, 2025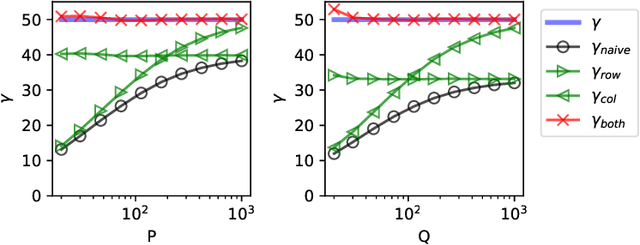
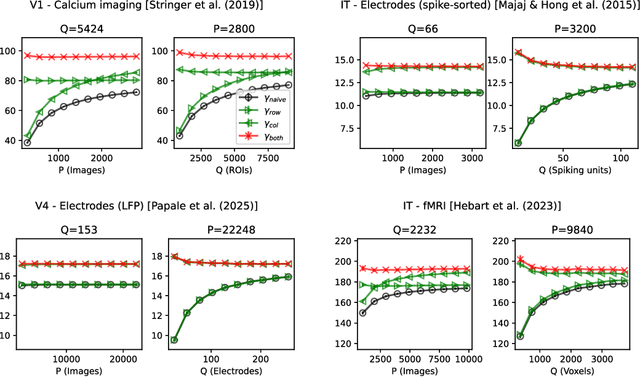
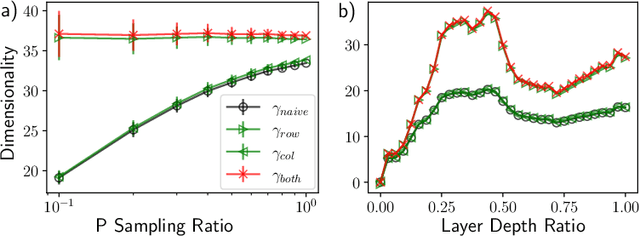
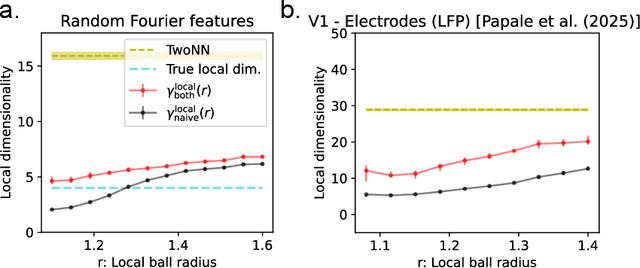
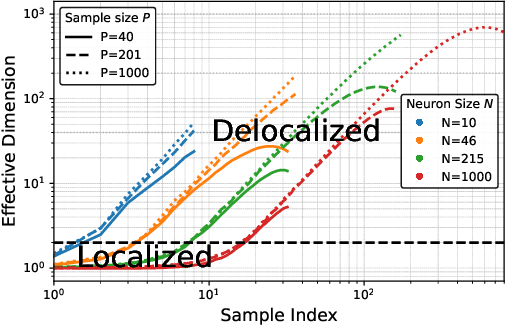
Abstract:The global dimensionality of a neural representation manifold provides rich insight into the computational process underlying both artificial and biological neural networks. However, all existing measures of global dimensionality are sensitive to the number of samples, i.e., the number of rows and columns of the sample matrix. We show that, in particular, the participation ratio of eigenvalues, a popular measure of global dimensionality, is highly biased with small sample sizes, and propose a bias-corrected estimator that is more accurate with finite samples and with noise. On synthetic data examples, we demonstrate that our estimator can recover the true known dimensionality. We apply our estimator to neural brain recordings, including calcium imaging, electrophysiological recordings, and fMRI data, and to the neural activations in a large language model and show our estimator is invariant to the sample size. Finally, our estimators can additionally be used to measure the local dimensionalities of curved neural manifolds by weighting the finite samples appropriately.
Spectral Analysis of Representational Similarity with Limited Neurons
Feb 27, 2025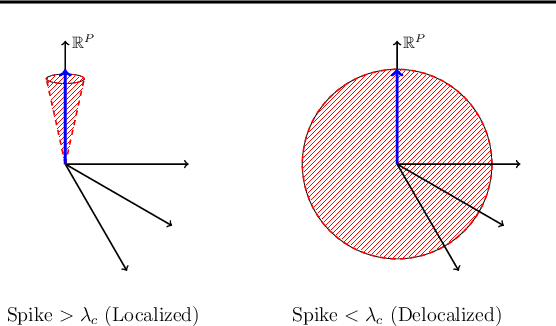
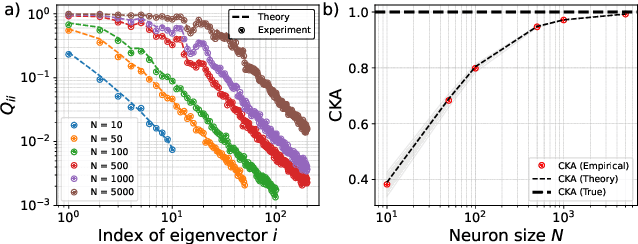
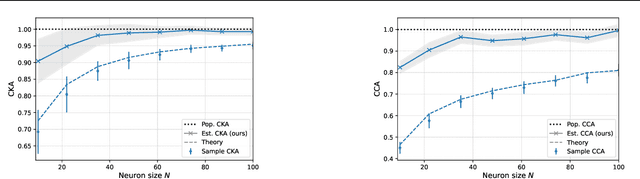
Abstract:Measuring representational similarity between neural recordings and computational models is challenging due to constraints on the number of neurons that can be recorded simultaneously. In this work, we investigate how such limitations affect similarity measures, focusing on Canonical Correlation Analysis (CCA) and Centered Kernel Alignment (CKA). Leveraging tools from Random Matrix Theory, we develop a predictive spectral framework for these measures and demonstrate that finite neuron sampling systematically underestimates similarity due to eigenvector delocalization. To overcome this, we introduce a denoising method to infer population-level similarity, enabling accurate analysis even with small neuron samples. Our theory is validated on synthetic and real datasets, offering practical strategies for interpreting neural data under finite sampling constraints.
Estimating Neural Representation Alignment from Limited Inputs and Features
Feb 20, 2025Abstract:In both artificial and biological systems, the centered kernel alignment (CKA) has become a widely used tool for quantifying neural representation similarity. While current CKA estimators typically correct for the effects of finite stimuli sampling, the effects of sampling a subset of neurons are overlooked, introducing notable bias in standard experimental scenarios. Here, we provide a theoretical analysis showing how this bias is affected by the representation geometry. We then introduce a novel estimator that corrects for both input and feature sampling. We use our method for evaluating both brain-to-brain and model-to-brain alignments and show that it delivers reliable comparisons even with very sparsely sampled neurons. We perform within-animal and across-animal comparisons on electrophysiological data from visual cortical areas V1, V4, and IT data, and use these as benchmarks to evaluate model-to-brain alignment. We also apply our method to reveal how object representations become progressively disentangled across layers in both biological and artificial systems. These findings underscore the importance of correcting feature-sampling biases in CKA and demonstrate that our bias-corrected estimator provides a more faithful measure of representation alignment. The improved estimates increase our understanding of how neural activity is structured across both biological and artificial systems.
The Geometry of Prompting: Unveiling Distinct Mechanisms of Task Adaptation in Language Models
Feb 11, 2025Abstract:Decoder-only language models have the ability to dynamically switch between various computational tasks based on input prompts. Despite many successful applications of prompting, there is very limited understanding of the internal mechanism behind such flexibility. In this work, we investigate how different prompting methods affect the geometry of representations in these models. Employing a framework grounded in statistical physics, we reveal that various prompting techniques, while achieving similar performance, operate through distinct representational mechanisms for task adaptation. Our analysis highlights the critical role of input distribution samples and label semantics in few-shot in-context learning. We also demonstrate evidence of synergistic and interfering interactions between different tasks on the representational level. Our work contributes to the theoretical understanding of large language models and lays the groundwork for developing more effective, representation-aware prompting strategies.
Statistical Mechanics of Support Vector Regression
Dec 06, 2024Abstract:A key problem in deep learning and computational neuroscience is relating the geometrical properties of neural representations to task performance. Here, we consider this problem for continuous decoding tasks where neural variability may affect task precision. Using methods from statistical mechanics, we study the average-case learning curves for $\varepsilon$-insensitive Support Vector Regression ($\varepsilon$-SVR) and discuss its capacity as a measure of linear decodability. Our analysis reveals a phase transition in the training error at a critical load, capturing the interplay between the tolerance parameter $\varepsilon$ and neural variability. We uncover a double-descent phenomenon in the generalization error, showing that $\varepsilon$ acts as a regularizer, both suppressing and shifting these peaks. Theoretical predictions are validated both on toy models and deep neural networks, extending the theory of Support Vector Machines to continuous tasks with inherent neural variability.
Estimating the Spectral Moments of the Kernel Integral Operator from Finite Sample Matrices
Oct 24, 2024Abstract:Analyzing the structure of sampled features from an input data distribution is challenging when constrained by limited measurements in both the number of inputs and features. Traditional approaches often rely on the eigenvalue spectrum of the sample covariance matrix derived from finite measurement matrices; however, these spectra are sensitive to the size of the measurement matrix, leading to biased insights. In this paper, we introduce a novel algorithm that provides unbiased estimates of the spectral moments of the kernel integral operator in the limit of infinite inputs and features from finitely sampled measurement matrices. Our method, based on dynamic programming, is efficient and capable of estimating the moments of the operator spectrum. We demonstrate the accuracy of our estimator on radial basis function (RBF) kernels, highlighting its consistency with the theoretical spectra. Furthermore, we showcase the practical utility and robustness of our method in understanding the geometry of learned representations in neural networks.
Towards an Improved Understanding and Utilization of Maximum Manifold Capacity Representations
Jun 13, 2024Abstract:Maximum Manifold Capacity Representations (MMCR) is a recent multi-view self-supervised learning (MVSSL) method that matches or surpasses other leading MVSSL methods. MMCR is intriguing because it does not fit neatly into any of the commonplace MVSSL lineages, instead originating from a statistical mechanical perspective on the linear separability of data manifolds. In this paper, we seek to improve our understanding and our utilization of MMCR. To better understand MMCR, we leverage tools from high dimensional probability to demonstrate that MMCR incentivizes alignment and uniformity of learned embeddings. We then leverage tools from information theory to show that such embeddings maximize a well-known lower bound on mutual information between views, thereby connecting the geometric perspective of MMCR to the information-theoretic perspective commonly discussed in MVSSL. To better utilize MMCR, we mathematically predict and experimentally confirm non-monotonic changes in the pretraining loss akin to double descent but with respect to atypical hyperparameters. We also discover compute scaling laws that enable predicting the pretraining loss as a function of gradients steps, batch size, embedding dimension and number of views. We then show that MMCR, originally applied to image data, is performant on multimodal image-text data. By more deeply understanding the theoretical and empirical behavior of MMCR, our work reveals insights on improving MVSSL methods.
Nonlinear classification of neural manifolds with contextual information
May 10, 2024



Abstract:Understanding how neural systems efficiently process information through distributed representations is a fundamental challenge at the interface of neuroscience and machine learning. Recent approaches analyze the statistical and geometrical attributes of neural representations as population-level mechanistic descriptors of task implementation. In particular, manifold capacity has emerged as a promising framework linking population geometry to the separability of neural manifolds. However, this metric has been limited to linear readouts. Here, we propose a theoretical framework that overcomes this limitation by leveraging contextual input information. We derive an exact formula for the context-dependent capacity that depends on manifold geometry and context correlations, and validate it on synthetic and real data. Our framework's increased expressivity captures representation untanglement in deep networks at early stages of the layer hierarchy, previously inaccessible to analysis. As context-dependent nonlinearity is ubiquitous in neural systems, our data-driven and theoretically grounded approach promises to elucidate context-dependent computation across scales, datasets, and models.
Neural Population Geometry and Optimal Coding of Tasks with Shared Latent Structure
Feb 26, 2024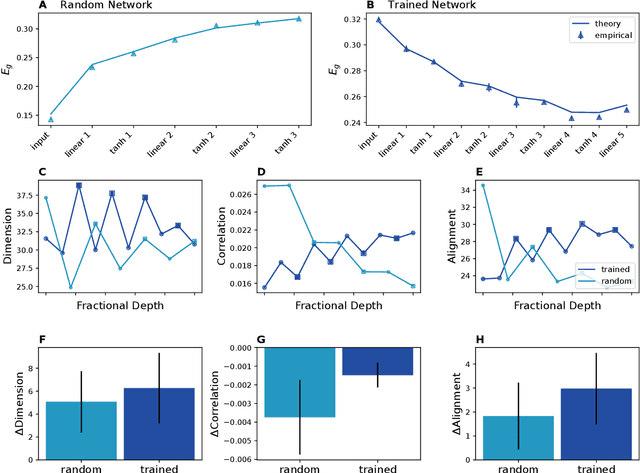
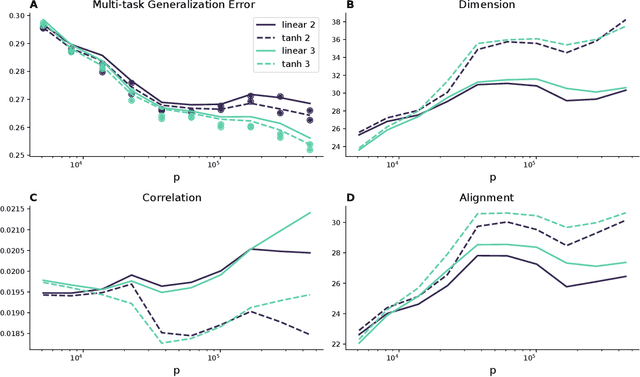
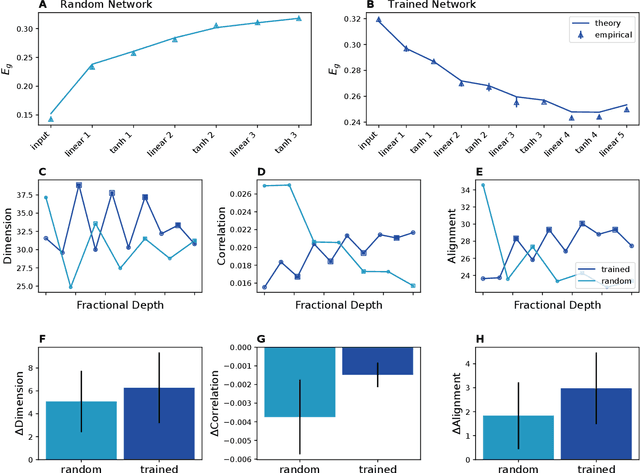
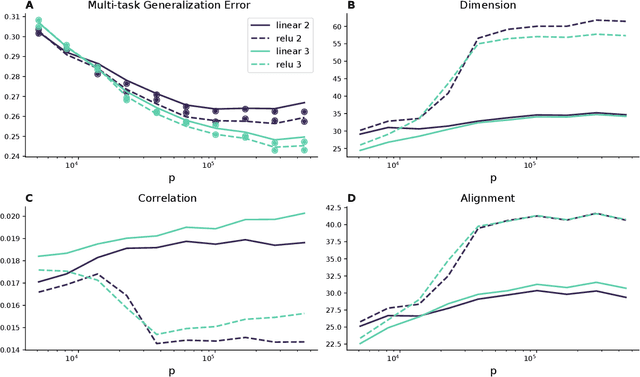
Abstract:Humans and animals can recognize latent structures in their environment and apply this information to efficiently navigate the world. Several recent works argue that the brain supports these abilities by forming neural representations that encode such latent structures in flexible, generalizable ways. However, it remains unclear what aspects of neural population activity are contributing to these computational capabilities. Here, we develop an analytical theory linking the mesoscopic statistics of a neural population's activity to generalization performance on a multi-task learning problem. To do this, we rely on a generative model in which different tasks depend on a common, unobserved latent structure and predictions are formed from a linear readout of a neural population's activity. We show that three geometric measures of the population activity determine generalization performance in these settings. Using this theory, we find that experimentally observed factorized (or disentangled) representations naturally emerge as an optimal solution to the multi-task learning problem. We go on to show that when data is scarce, optimal codes compress less informative latent variables, and when data is abundant, optimal codes expand this information in the state space. We validate predictions from our theory using biological and artificial neural network data. Our results therefore tie neural population geometry to the multi-task learning problem and make normative predictions of the structure of population activity in these settings.
Probing Biological and Artificial Neural Networks with Task-dependent Neural Manifolds
Dec 21, 2023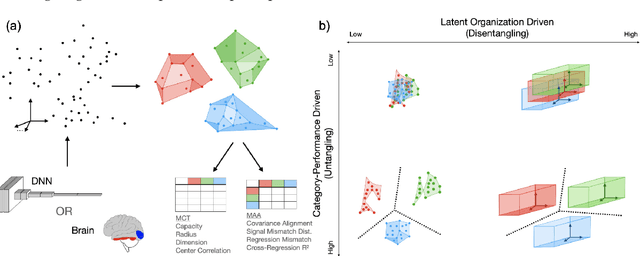
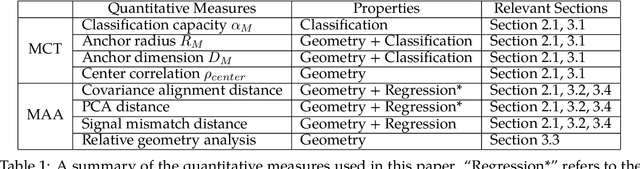
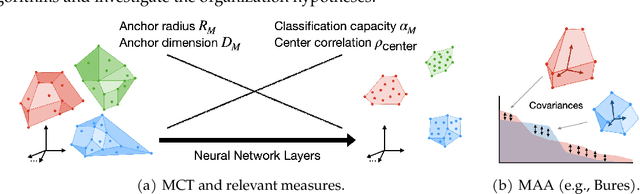

Abstract:Recently, growth in our understanding of the computations performed in both biological and artificial neural networks has largely been driven by either low-level mechanistic studies or global normative approaches. However, concrete methodologies for bridging the gap between these levels of abstraction remain elusive. In this work, we investigate the internal mechanisms of neural networks through the lens of neural population geometry, aiming to provide understanding at an intermediate level of abstraction, as a way to bridge that gap. Utilizing manifold capacity theory (MCT) from statistical physics and manifold alignment analysis (MAA) from high-dimensional statistics, we probe the underlying organization of task-dependent manifolds in deep neural networks and macaque neural recordings. Specifically, we quantitatively characterize how different learning objectives lead to differences in the organizational strategies of these models and demonstrate how these geometric analyses are connected to the decodability of task-relevant information. These analyses present a strong direction for bridging mechanistic and normative theories in neural networks through neural population geometry, potentially opening up many future research avenues in both machine learning and neuroscience.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge