Neural Population Geometry and Optimal Coding of Tasks with Shared Latent Structure

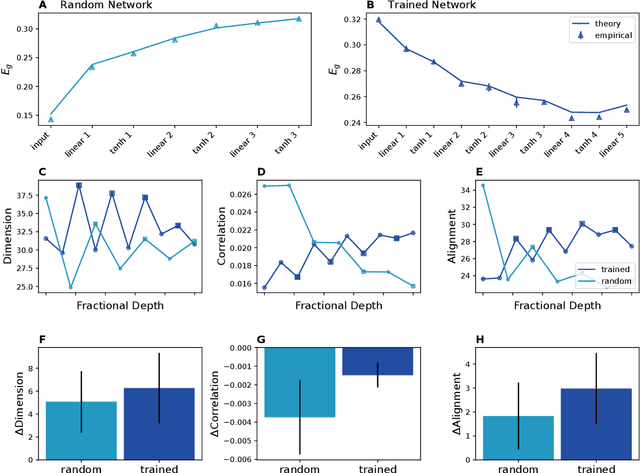
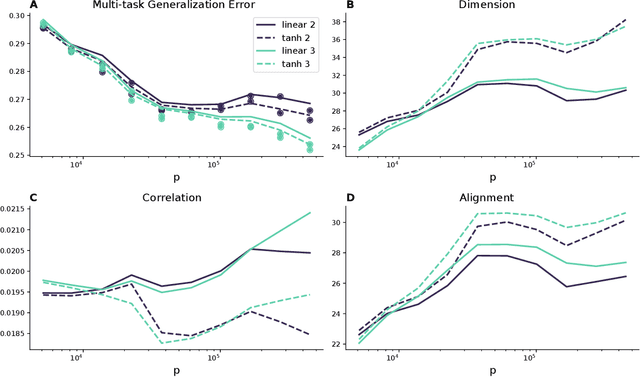
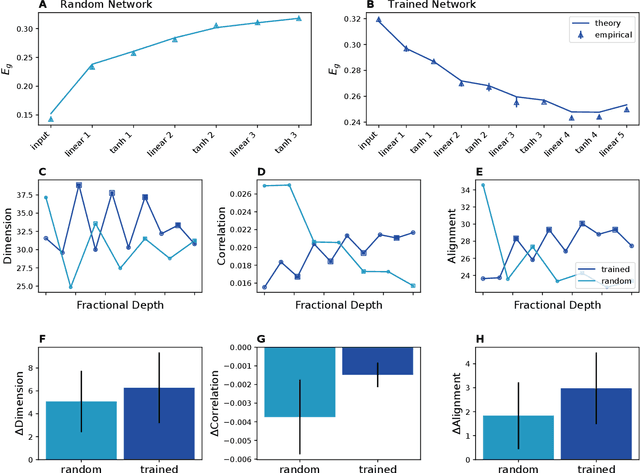
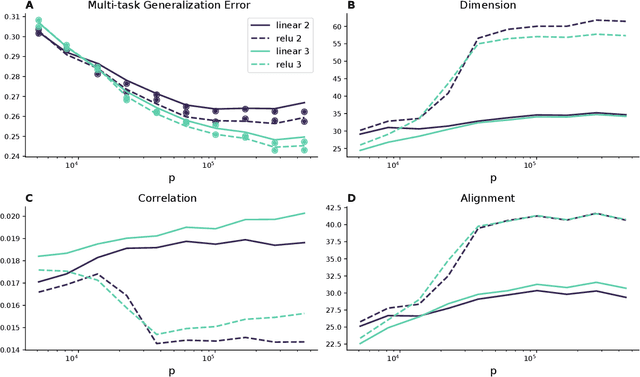
Humans and animals can recognize latent structures in their environment and apply this information to efficiently navigate the world. Several recent works argue that the brain supports these abilities by forming neural representations that encode such latent structures in flexible, generalizable ways. However, it remains unclear what aspects of neural population activity are contributing to these computational capabilities. Here, we develop an analytical theory linking the mesoscopic statistics of a neural population's activity to generalization performance on a multi-task learning problem. To do this, we rely on a generative model in which different tasks depend on a common, unobserved latent structure and predictions are formed from a linear readout of a neural population's activity. We show that three geometric measures of the population activity determine generalization performance in these settings. Using this theory, we find that experimentally observed factorized (or disentangled) representations naturally emerge as an optimal solution to the multi-task learning problem. We go on to show that when data is scarce, optimal codes compress less informative latent variables, and when data is abundant, optimal codes expand this information in the state space. We validate predictions from our theory using biological and artificial neural network data. Our results therefore tie neural population geometry to the multi-task learning problem and make normative predictions of the structure of population activity in these settings.

Linear Classification of Neural Manifolds with Correlated Variability

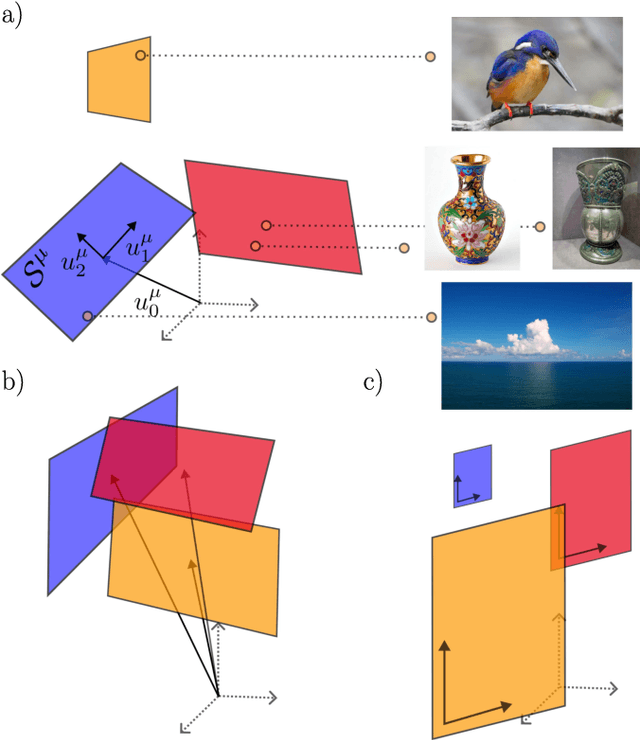
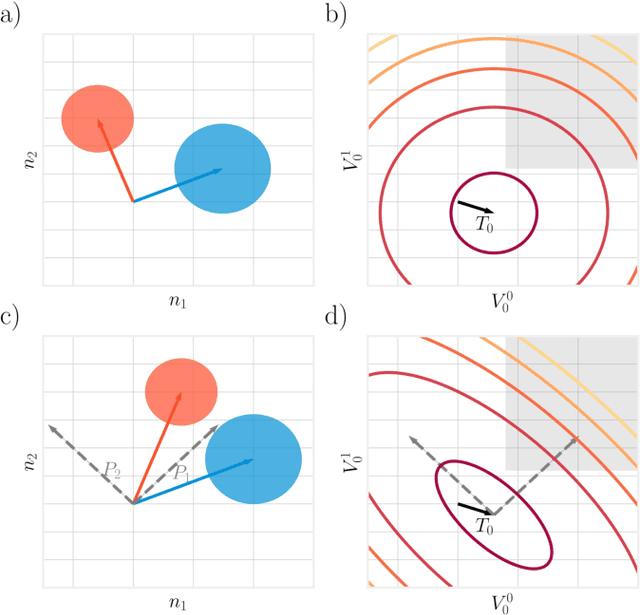
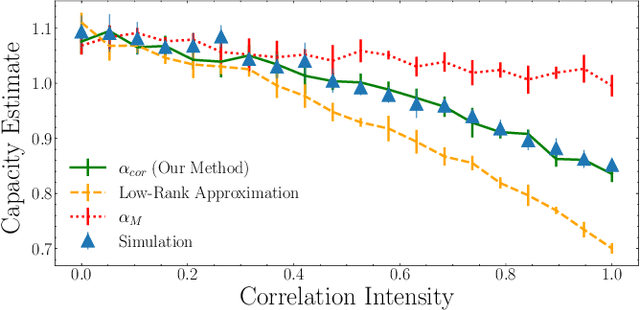
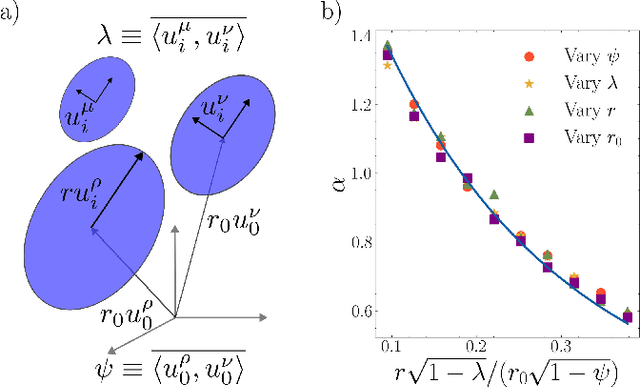
Understanding how the statistical and geometric properties of neural activations relate to network performance is a key problem in theoretical neuroscience and deep learning. In this letter, we calculate how correlations between object representations affect the capacity, a measure of linear separability. We show that for spherical object manifolds, introducing correlations between centroids effectively pushes the spheres closer together, while introducing correlations between the spheres' axes effectively shrinks their radii, revealing a duality between neural correlations and geometry. We then show that our results can be used to accurately estimate the capacity with real neural data.