Linear Classification of Neural Manifolds with Correlated Variability

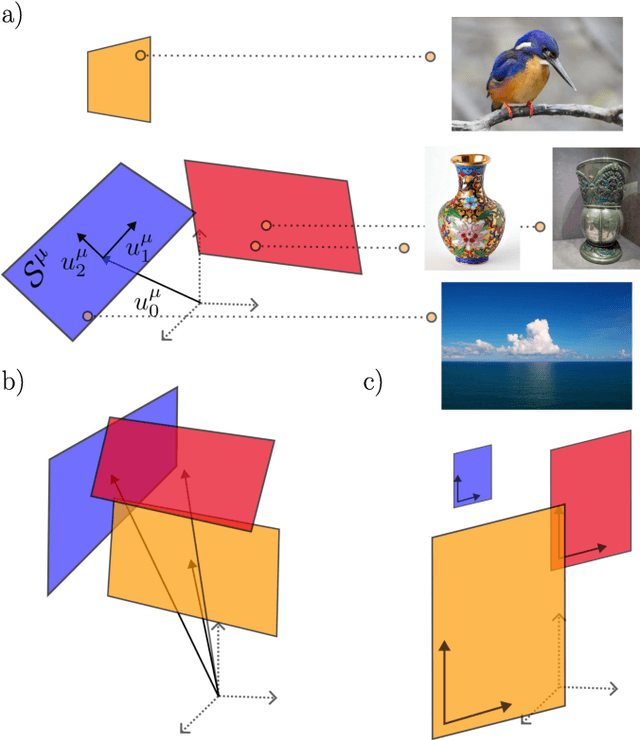
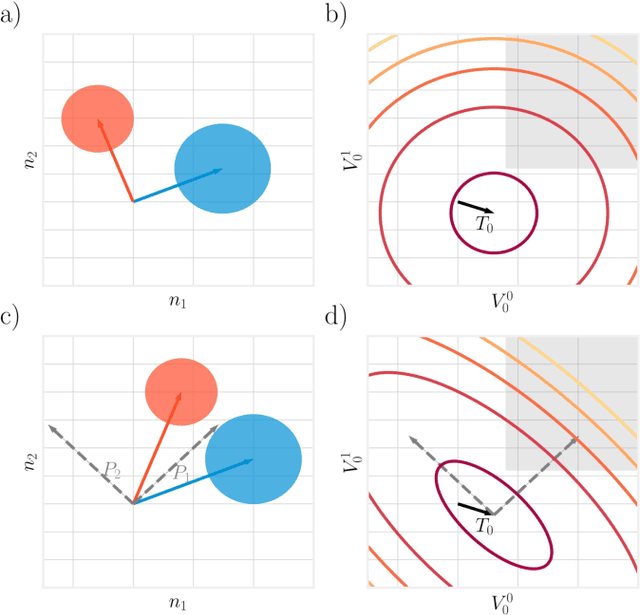
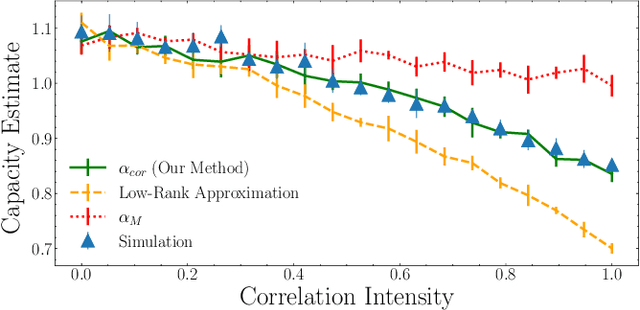
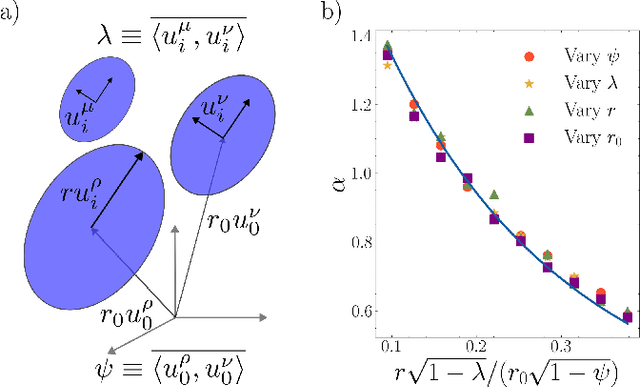
Understanding how the statistical and geometric properties of neural activations relate to network performance is a key problem in theoretical neuroscience and deep learning. In this letter, we calculate how correlations between object representations affect the capacity, a measure of linear separability. We show that for spherical object manifolds, introducing correlations between centroids effectively pushes the spheres closer together, while introducing correlations between the spheres' axes effectively shrinks their radii, revealing a duality between neural correlations and geometry. We then show that our results can be used to accurately estimate the capacity with real neural data.