Nonlinear classification of neural manifolds with contextual information

Understanding how neural systems efficiently process information through distributed representations is a fundamental challenge at the interface of neuroscience and machine learning. Recent approaches analyze the statistical and geometrical attributes of neural representations as population-level mechanistic descriptors of task implementation. In particular, manifold capacity has emerged as a promising framework linking population geometry to the separability of neural manifolds. However, this metric has been limited to linear readouts. Here, we propose a theoretical framework that overcomes this limitation by leveraging contextual input information. We derive an exact formula for the context-dependent capacity that depends on manifold geometry and context correlations, and validate it on synthetic and real data. Our framework's increased expressivity captures representation untanglement in deep networks at early stages of the layer hierarchy, previously inaccessible to analysis. As context-dependent nonlinearity is ubiquitous in neural systems, our data-driven and theoretically grounded approach promises to elucidate context-dependent computation across scales, datasets, and models.

Probing Biological and Artificial Neural Networks with Task-dependent Neural Manifolds

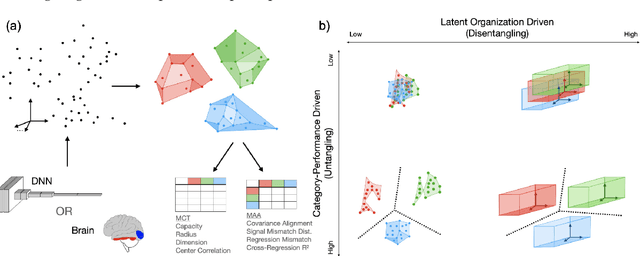
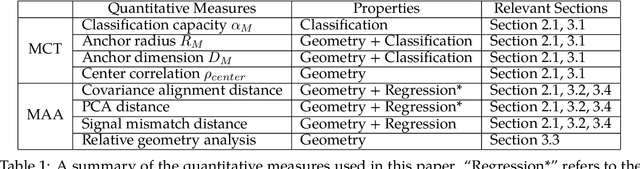
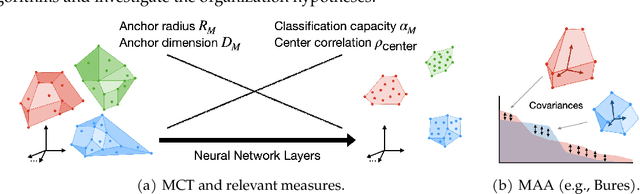
Recently, growth in our understanding of the computations performed in both biological and artificial neural networks has largely been driven by either low-level mechanistic studies or global normative approaches. However, concrete methodologies for bridging the gap between these levels of abstraction remain elusive. In this work, we investigate the internal mechanisms of neural networks through the lens of neural population geometry, aiming to provide understanding at an intermediate level of abstraction, as a way to bridge that gap. Utilizing manifold capacity theory (MCT) from statistical physics and manifold alignment analysis (MAA) from high-dimensional statistics, we probe the underlying organization of task-dependent manifolds in deep neural networks and macaque neural recordings. Specifically, we quantitatively characterize how different learning objectives lead to differences in the organizational strategies of these models and demonstrate how these geometric analyses are connected to the decodability of task-relevant information. These analyses present a strong direction for bridging mechanistic and normative theories in neural networks through neural population geometry, potentially opening up many future research avenues in both machine learning and neuroscience.

A General Framework for Analyzing Stochastic Dynamics in Learning Algorithms

We present a general framework for analyzing high-probability bounds for stochastic dynamics in learning algorithms. Our framework composes standard techniques such as a stopping time, a martingale concentration and a closed-from solution to give a streamlined three-step recipe with a general and flexible principle to implement it. To demonstrate the power and the flexibility of our framework, we apply the framework on three very different learning problems: stochastic gradient descent for strongly convex functions, streaming principal component analysis and linear bandit with stochastic gradient descent updates. We improve the state of the art bounds on all three dynamics.

ODE-Inspired Analysis for the Biological Version of Oja's Rule in Solving Streaming PCA

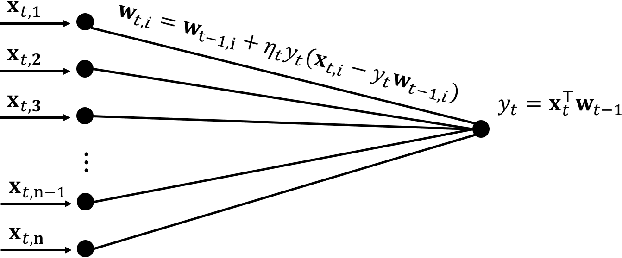
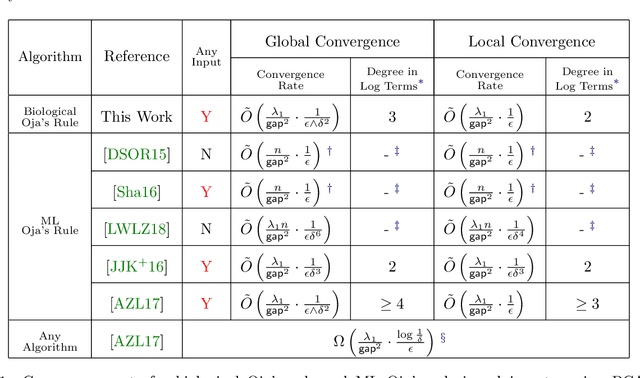
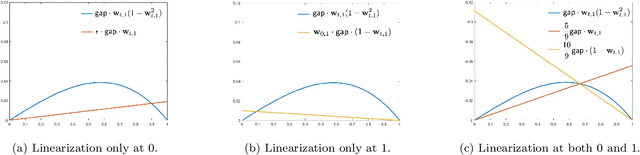
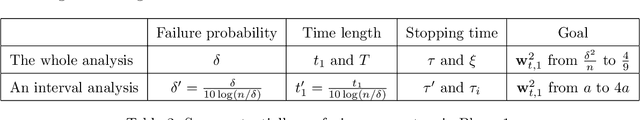
Oja's rule [Oja, Journal of mathematical biology 1982] is a well-known biologically-plausible algorithm using a Hebbian-type synaptic update rule to solve streaming principal component analysis (PCA). Computational neuroscientists have known that this biological version of Oja's rule converges to the top eigenvector of the covariance matrix of the input in the limit. However, prior to this work, it was open to prove any convergence rate guarantee. In this work, we give the first convergence rate analysis for the biological version of Oja's rule in solving streaming PCA. Moreover, our convergence rate matches the information theoretical lower bound up to logarithmic factors and outperforms the state-of-the-art upper bound for streaming PCA. Furthermore, we develop a novel framework inspired by ordinary differential equations (ODE) to analyze general stochastic dynamics. The framework abandons the traditional step-by-step analysis and instead analyzes a stochastic dynamic in one-shot by giving a closed-form solution to the entire dynamic. The one-shot framework allows us to apply stopping time and martingale techniques to have a flexible and precise control on the dynamic. We believe that this general framework is powerful and should lead to effective yet simple analysis for a large class of problems with stochastic dynamics.

(Nearly) Efficient Algorithms for the Graph Matching Problem on Correlated Random Graphs

We give a quasipolynomial time algorithm for the graph matching problem (also known as noisy or robust graph isomorphism) on correlated random graphs. Specifically, for every $\gamma>0$, we give a $n^{O(\log n)}$ time algorithm that given a pair of $\gamma$-correlated $G(n,p)$ graphs $G_0,G_1$ with average degree between $n^{\varepsilon}$ and $n^{1/153}$ for $\varepsilon = o(1)$, recovers the "ground truth" permutation $\pi\in S_n$ that matches the vertices of $G_0$ to the vertices of $G_n$ in the way that minimizes the number of mismatched edges. We also give a recovery algorithm for a denser regime, and a polynomial-time algorithm for distinguishing between correlated and uncorrelated graphs. Prior work showed that recovery is information-theoretically possible in this model as long the average degree was at least $\log n$, but sub-exponential time algorithms were only known in the dense case (i.e., for $p > n^{-o(1)}$). Moreover, "Percolation Graph Matching", which is the most common heuristic for this problem, has been shown to require knowledge of $n^{\Omega(1)}$ "seeds" (i.e., input/output pairs of the permutation $\pi$) to succeed in this regime. In contrast our algorithms require no seed and succeed for $p$ which is as low as $n^{o(1)-1}$.

On the Algorithmic Power of Spiking Neural Networks

Spiking Neural Networks (SNN) are mathematical models in neuroscience to describe the dynamics among a set of neurons which interact with each other by firing spike signals to each other. Interestingly, recent works observed that for an integrate-and-fire model, when configured appropriately (e.g., after the parameters are learned properly), the neurons' firing rate, i.e., converges to an optimal solution of Lasso and certain quadratic optimization problems. Thus, SNN can be viewed as a natural algorithm for solving such convex optimization problems. However, theoretical understanding of SNN algorithms remains limited. In particular, only the convergence result for the Lasso problem is known, but the bounds of the convergence rate remain unknown. Therefore, we do not know any explicit complexity bounds for SNN algorithms. In this work, we investigate the algorithmic power of the integrate-and-fire SNN model after the parameters are properly learned/configured. In particular, we explore what algorithms SNN can implement. We start by formulating a clean discrete-time SNN model to facilitate the algorithmic study. We consider two SNN dynamics and obtain the following results. * We first consider an arguably simplest SNN dynamics with a threshold spiking rule, which we call simple SNN. We show that simple SNN solves the least square problem for a matrix $A\in\mathbb{R}^{m\times n}$ and vector $\mathbf{b} \in \mathbb{R}^m$ with timestep complexity $O(\kappa n/\epsilon)$. * For the under-determined case, we observe that simple SNN may solve the $\ell_1$ minimization problem using an interesting primal-dual algorithm, which solves the dual problem by a gradient-based algorithm while updates the primal solution along the way. We analyze a variant dynamics and use simulation to serve as partial evidence to support the conjecture.